神经元Chay模型簇放电活动的分岔研究
周 毅
(淮南师范学院 数学与计算科学系,安徽 淮南 232038)
神经元Chay模型簇放电活动的分岔研究
周 毅
(淮南师范学院 数学与计算科学系,安徽 淮南 232038)
对于神经元Chay模型,数值仿真了不同参数条件下,系统出现的四种典型的簇放电活动,得出了神经元簇放电活动中四类不同的模式:fold/fold滞后环的fold/Hopf型、fold/fold点-点滞后环型、fold/homoclinic滞后环的Hopf/homoclinic型、fold/homoclinic滞后环fold/homoclinic型,并应用快慢动力学分岔分析方法,研究了它们的动力学行为和产生机制.
神经元;簇放电;仿真;分岔;快慢动力学
1 引言
生物神经系统是具有快慢时间尺度的动力系统,是高度复杂的非线性系统,因此神经系统能产生纷繁多样的非线性现象.神经元作为神经系统的基本功能单位,通过不同放电模式(如周期或者混沌的峰放电和簇放电)对外界刺激信息进行编码、传递和解码,这其中簇放电是神经元放电活动的主要模式.实际的神经元簇放电活动是多种多样的,而且不同类型簇放电模式的计算性质[1,2]也是各不相同的.
神经元簇放电活动的动力学行为和模式划分是近些年来发展起来的新兴学科神经动力学研究的一个重点,并且在很多电生理实验和理论研究中[3-8]都被着重探讨.在国际上Rinzel,Izhikevich等学者应用分岔理论对神经元放电的各种模式及动力学行为进行了分类和研究,得出了方波形、椭圆形、抛物形、三角形等簇放电模式;在国内裴利军,王永刚,范晔对Chay模型平衡点与周期解的稳定性作了定性分析;杨卓琴、陆启韶以Chay模型为对象,对快子系统的分岔曲线上,具有一个、两个以及没有Hopf点时的簇放电模式进行了分类.本文主要针对神经元Chay模型,通过数值仿真,利用快慢动力学分岔分析[9,10]的方法来研究其簇放电活动,得出了四种簇放电模式,并对四种模式作了更细致的分类.
2 模型介绍
Chay模型是1985年,基于与Ca2+有关的K+通道起重要作用的许多不同类型的可兴奋性细胞,如神经元、冷觉感受器、心肌细胞、感觉末梢等,建立的具有高度统一性的理论模型.该模型能模拟可兴奋细胞的各种激发模式,具有较高的生物和理性.本文考虑的是具有外界去极化电流的Chay模型:

其中 (1)式表示细胞膜电位V的变化所遵循的微分方程,等号右边四项分别为混合Na+-Ca2+通道中的电流、电导依赖电位的K+离子通道电流、电导不依赖电位而依赖细胞膜内Ca2+浓度的K离子通道电流和漏电流;Vk,VI和VL分别是K+离子通道、混合Na+-Ca2+离子通道和漏电离子通道的可逆电位;gI,gk,v,gk,c和gL分别代表各通道的最大电导.(2)式表示依赖于电位的K离子通道打开的概率的变化规律,其中τn是弛豫时间.(3)式表示细胞膜内Ca2+浓度的变化规律,右边两项分别表示进出膜的Ca2+通道电流;Kc是细胞内Ca2+流出的比率常数,ρ是比例性常数,Vc是钙离子通道的可逆电位.方程 (1)-(3)中的m∞和h∞分别是混合Na+-Ca2+通道激活和失活的概率的稳态值,n∞为n的稳定态值,它们的具体表达式为:
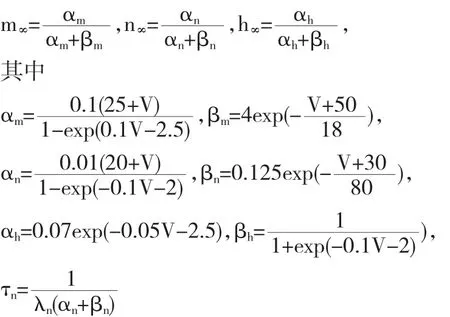
其中λn是与K离子通道的时间常数相关的参数.
在快慢动力学分岔分析中,由于Chay系统(3)中ρ一般取很小的值,因此细胞内Ca2+离子浓度C随时间变化的速度比其它变量要慢很多,所以我们取(4.4)、(4.5)为快变子系统,(4.6)为慢变子系统,慢变量C视为为快变子系统的分岔参数.
快变子系统平衡点的分岔曲线方程如下:

各参数取值如下:
gI=1800,gK,V=1700,gK,C=10,gL=7,VI=100,VL=-40,ρ=0.27;而λn,VC,VK,I取为控制参数.
3 结果
3.1 经由fold/fold滞后环的fold/Hopf型簇放电
当λn=350,VC=101,VK=-109,I=0时,我们得到如图1所示的时序图与分岔图.
如图1(b),快变子系统的平衡点就其分岔参数C的不同的值,形成在相平面上的一条Z形的分岔曲线,并且将图1(a)的簇放电轨线叠加于图中.在快变子系统的Z形分岔曲线的上支有两个Hopf分岔点产生H1和H2.这样,快变子系统分岔曲线上支的稳定焦点 (实线)经由点H1处的超临界Hopf分岔而失稳成为不稳定焦点(虚线),同时快变子系统的稳定极限环(实曲线)在不稳定分岔曲线上支周围产生,用Vmax和Vmin表示其膜电位的最大值和最小值;随着慢变量C的增加,快系统的稳定极限环经由点H2处的超临界Hopf分岔消失而转变为稳定焦点(实线).快变子系统分岔曲线的中支和下支,分别由鞍点(虚线)以及稳定结点(实线)组成.
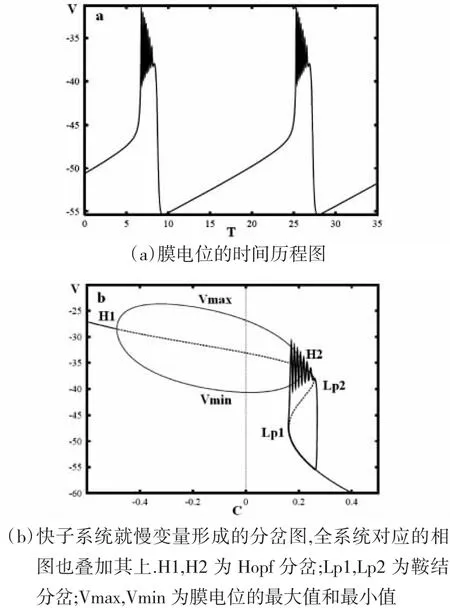
图1
随着参数C的减小,相应于快变子系统分岔曲线下支稳定结点的簇放电的静息态,经由鞍结分岔LP1消失,并转迁到Z形分岔曲线上支周围稳定极限环的放电状态.随着参数C的增加,放电状态相应的快变子系统的稳定极限环经由Hopf分岔H2转变为稳定焦点,因此H2后的簇放电轨线以逐渐衰减的振荡方式收敛于稳定焦点,然后经由鞍结分岔Lp2转迁到快变子系统分岔曲线下支的静息状态.这一过程周期性的反复进行,引起了簇放电的两种状态的相互转迁,其中静息状态转迁到放电状态的分岔(即放电状态产生的分岔)是Lp1处的鞍结分岔,而放电状态转迁到静息状态的分岔(即放电状态结束的分岔)是H2处的Hopf分岔.根据快慢动力学分析的分类方法,此簇放电模式称为fold/Hopf型簇放电.
此外除了上述这两种与放电状态产生或结束有关的分岔外,还有引起滞后环产生的分岔,即从簇放电的下状态转迁到上状态的分岔为Lp1处的鞍结分岔和从簇放电的上状态转迁到下状态的分岔为Lp2处的鞍结分岔.因此,此时簇放电模式表现出经由fold/fold滞后环的fold/Hopf型簇放电的动力学性质.
3.2 fold/fold点-点滞后环型簇放电
当 λn=400,VC=101,VK=-109,I=0时,我们得到如图 2所示的时序图与分岔图.

图2
如图2(b),快变子系统的平衡点就其分岔参数C的不同的值,形成在相平面上的一条Z形的分岔曲线,并且将图2(a)的簇放电轨线叠加于图中.尽管快变子系统上支有两个Hopf分岔点,稳定极限环产生于它们之间;但随着分岔参数C的减小,位于快变子系统分岔曲线下支的由稳定结点代表的下静息态经由鞍结分岔Lp1消失,进而转迁到Z形分岔曲线上支的由稳定焦点构成的上静息态,并未转迁到相应于稳定极限环的稳定放电状态.随着分岔参数C的增加,上静息态经由鞍结分岔Lp2消失,重新转迁到下静息态.一个点-点滞后环由两个静息态(快变子系统分岔曲线上稳定的上状态与稳定的下状态)之间的相互转迁产生.
因此,该簇放电模式表现出fold/fold点-点滞后环型簇放电的动力学性质.
3.3 经由fold/homoclinic滞后环的Hopf/homoclinic型簇放电
当 λn=230,VC=335,VK=-60,I=-65 时,我们得到如图 3所示的时序图与分岔图.
快变子系统的平衡点就其分岔参数C的不同的值,形成在相平面上L形与抛物线C形的两条分岔曲线,并且将图3(a)的簇放电轨线叠加于图中.在L形分岔曲线上,稳定焦点经由Hopf分岔点H失稳,稳定极限环在不稳定焦点周围形成,Vmax和Vmin表示其膜电位的最大值和最小值.C形分岔曲线上下支分别为鞍点(虚线)与稳定结点(实线),它们经由鞍结分岔点Lp合并消失.
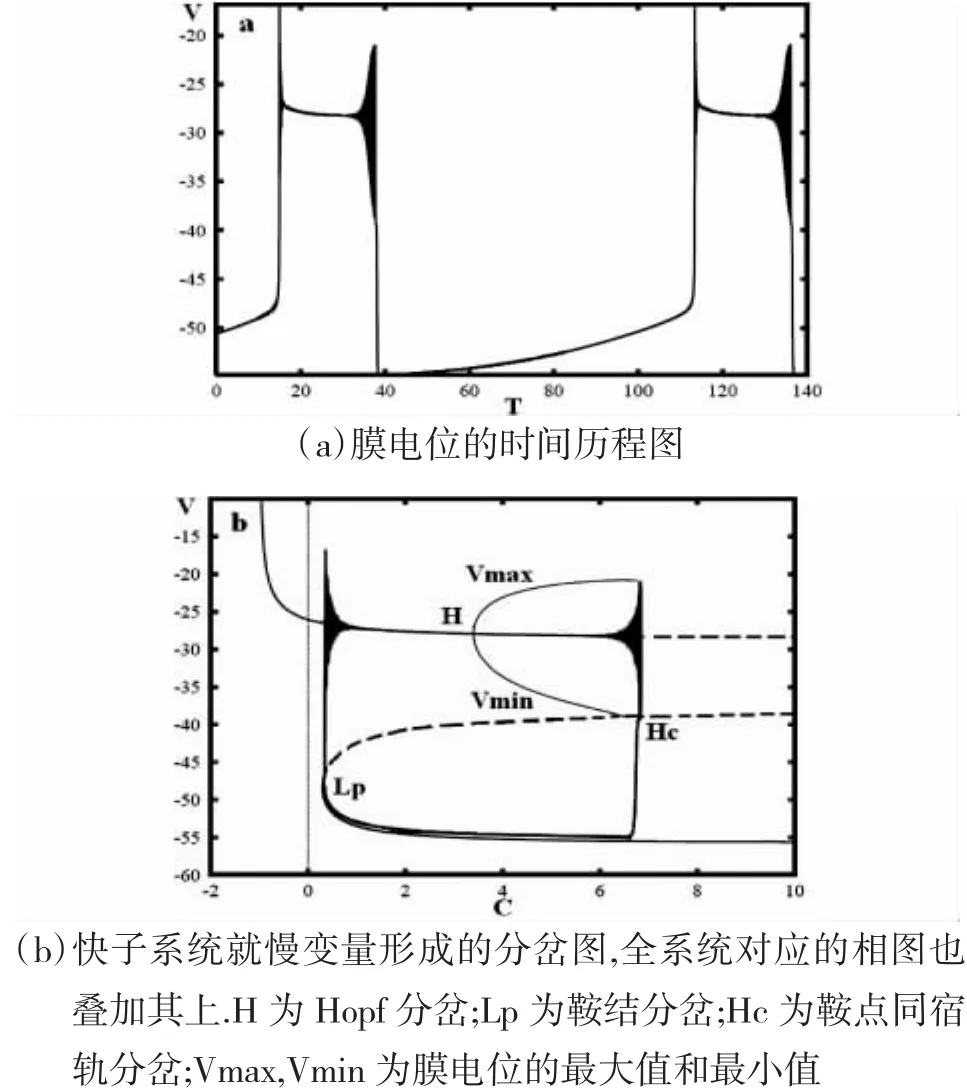
图3
如图3(b),随着参数C的减小,相应于快变子系统C形分岔曲线下支稳定结点的簇放电的下静息态,经由鞍结分岔Lp消失,并转迁到L形分岔曲线上支稳定焦点的上静息态.上静息态振幅衰减的振荡是簇振荡轨线收敛于稳定焦点的结果.随着参数C的增加,上静息态经由Hopf分岔点H结束而开始反复连续的放电状态.随着分岔参数C的继续增加,稳定极限环碰到C形分岔曲线上支的鞍点,形成鞍点同宿轨分岔Hc,从而反复放电状态经由Hc结束,进而转迁到由稳定结点表示的下静息态.
因此,该簇放电模式表现出经由fold/homoclinic滞后环的Hopf/homoclinic型簇放电的动力学性质.
3.4 经由fold/homoclinic滞后环的fold/homoclinic型簇放电

图4
当 λn=230,VC=100,VK=-65,I=-65 时,我们得到如图 4所示的时序图与分岔图.
快变子系统的平衡点就其分岔参数C的不同的值,形成在相平面上L形与抛物线C形的两条分岔曲线,并且将图4(a)的簇放电轨线叠加于图中.
如图4(b),随着分岔参数C的减小,相应于快变子系统C形分岔曲线下支稳定结点的簇放电的下静息态,经由鞍结分岔Lp消失,并转迁到L形分岔曲线上相应于稳定极限环的簇放电状态.随着分岔参数C的增加,轨线沿鞍点同宿轨Hc回到鞍点,进而转迁到下静息状态.因此,静息态转迁到重复峰放电状态的分岔Lp处的鞍结分岔,重复峰放电状态转迁到静息态的分岔是鞍点同宿轨分岔Hc.另外,产生滞后环的分岔与放电开始与结束的分岔是一致的.
因此,此簇放电模式表现出fold/homoclinic滞后环的fold/homoclinic型簇放电的动力学性质.
4 讨论
本文通过数值仿真,得出了神经元Chay模型在不同参数条件下的四种典型簇放电模式.通过快慢动力学分岔分析,对不同的放电模式进行了分类,系统的研究各放电模式的动力学行为,进一步揭示了经由fold/fold滞后环的fold/Hopf型、fold/fold点-点滞后环型、fold/homoclinic滞后环 的 Hopf/homoclinic型 、fold/homoclinic滞 后 环fold/homoclinic型,四种不同类型的簇放电模式产生的机制.然而由于现实背景下的簇放电模式是多种多样的,我们还需要找出神经元模型中更多类型的簇放电模式并研究它们的动力学行为和机制.同时由于神经系统信息编码的复杂性,时滞、噪声等对于神经元的放电活动的影响也是下一步需要研究的问题.
〔1〕Fall C.P..Computational cell biology[M].New York:Springer-Verlag,2002.
〔2〕Izhikevich E. M. Mathematical foundations of neuroscience[M].New York:Springer,2010.
〔3〕Izhikevich E.M. Neuralexcitability,spiking and bursting [J]. Int. J. Bifurcat. Chaos, 2000, 10:1171-1266.
〔4〕杨卓琴,陆启韶.神经元Chay模型中不同类型的簇放电模式 [J].中国科学G辑:物理学 力学 天文学,2007(37):440-450.
〔5〕裴利军,王永刚,范晔.神经元Chay模型的动力学分析[J].郑州大学学报,2009(41):7-12.
〔6〕Chay T.R.Chaos in a three-variable model of an excitable cell.[J].Physica D,1985,16:233-242.
〔7〕Chay T.R.,Rinzel J.Bursting,beating and chaos in an excitable membrane model [J].Biophys.1985,47:357-366.
〔8〕Chay T.R.Electrical bursting and luminal calcium oscillation in excitable cellmodels [J]. Biological cybernetics,1996,75:419-431.
〔9〕Rinzel J.Bursting oscillation in an excitable membrane model in ordinary and partial diferential equations[M].Berlin:Springer-Verlag,1985.
〔10〕ErmentroutB.Simulating,analyzing,and animating dynamical systems[M].Philadelphia:SIAM,2002.
O193
A
1673-260X(2012)06-0023-03
安徽高校省级自然科学研究项目(KJ2012A257);安徽省优秀青年基金(2010SQRL167);淮南师范学院青年教师基金(2012LK17)

