约束优化的粒子群改进算法及应用

李二闷，卫良保，李 扬，张玉星，马朝选

(太原科技大学机械工程学院，太原 030024)

在科学计算与实际工程优化领域，许多优化问题都可以归结为约束优化问题，而且约束优化问题的求解要比无约束优化优化问题的复杂困难，因此，研究如何处理约束优化问题并能得到最优解具有很重要的实际意义。1995年，Eberhart和Kennedy提出的粒子群优化算法(PSO)是一种基于种群搜索策略的现代智能优化算法[1]。由于其具有易理解、易实现、不要求目标函数和约束条件可微，并能以较大概率求得全局最优解的特点，目前已成功应用于神经网络权值的训练、连续和离散系统的参数优化及求解组合优化问题等许多优化问题[2]。但粒子群算法也表现出了求解成功率不高，易于坠入局部最优解，早熟等不足。

近些年来，国内外相关学者针对粒子群的不足，对粒子群进行改进，改进措施大致分为两类，一是从对算法本身改进，提高PSO单一方面的优化性能，例如惯性权重法、压缩因子法、混合法等，任子晖、王坚于2009年提出了基于聚集距离变化率的自适应惯性权重PSO算法;二是与其它算法思想的组合，使得算法的优化效果在一定程度上得到提高，Angeline和Lovbjerg提出了基于遗传思想改进的粒子群算法，2004年高鹰等提出了基于模拟退火的粒子群算法，2008年，ShengLi Song和Li Kong等人，提出了结合模拟退火和单纯形法混合粒子群算法。

结合PSO算法及约束优化问题的特点，并针对PSO算法本身的局限性，为了减少判断约束条件所需的时间，提高优化精确度、成功率，引入回退算法思想，并用直接解法，提出了一种新的求解约束优化问题的改进(advanced)的PSO算法——APSO.计算实例表明APSO算法具有更强的寻优能力和效率。

1 基本粒子群算法

在标准PSO算法中，优化问题被抽象成为一群粒子相互支持学习去寻找空间中的最优位置，而粒子都有一个被目标函数所决定的适应度值(Fitness Value)，一个决定它们位置和飞行方向的速度，然后粒子们就以该速度追随当前的最优粒子在解空间中进行搜索，其中，粒子的飞行速度根据个体的飞行经验和群体的飞行经验进行动态的调整。假设 Xi=(xi1，xi2，…，xin) 是微粒 i的当前位置，Vi=(vi，1，vi，2，…，vi，n) 是微粒 i的当前飞行速度，那么，基本粒子群算法的进化方程如下:

基本微粒群算法的流程如图1[3]:

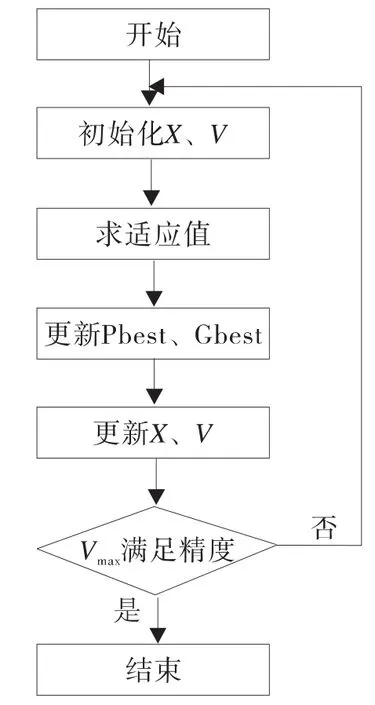
图1 粒子群算法流程图Fig.1 The flowchart of PSO

2 改进粒子群算法

在处理约束条件时，参考直接法，若不满足约束的粒子被直接丢弃删除，就不能保持好粒子群的完整性和粒子的多样性，而且若抛弃的粒子过多，空间搜索区域的粒子密度就会降低，在后继的搜索中，平均单个粒子的探索区域就扩大，由于每一次搜索的步长没有变化，那么迭代次数就会增加，搜索时间就相应的变长，造成求解速度过慢;由于粒子数目过少，那么只能从仅有的几个粒子中寻找最优，备选方案就大大减少，易于陷入局部最优，更有甚者，若所有的粒子不合工程约束，就得全部丢弃，那么本次优化只能以失败而告终。

引入回退的思想，对于进化过程中不满足约束条件的粒子实行改造。改造时，不合格粒子回退到的该粒子历史最优位置再参与到下一轮的进化，不仅能较好地保持多样性、完整性，而且收敛速度快，优化成功率也升至100%.表达式表示为:

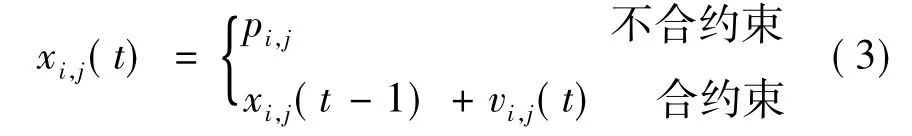
改进粒子群算法的具体算法流程如下，其中Step6体现了APSO的核心:

step1，依照初始化过程，对微粒群的随机位置和速度进行初始化并对每个粒子进行约束函数判断，若不满足，则重新初始化该粒子;

step2，计算每个微粒的适应值;

Step3，对每个微粒，将其适应值与所经历过的最好位置的适应值进行比较，若较好，则将其作为当前的最好位置;

step4，对每个微粒，将其适应值与全局所经历的最好位置的适应值进行比较，若较好，则将其作为当前的全局最好位置;

step5，根据进化方程对微粒速度和位置进行优化;

step6，判断新的位置是否满足实际工程约束函数，若不满足，用粒子历史最优位置替代当前位置，以方便下一次搜索时的搜索路径的改变;

step7，如未达到结束条件，则返回step2.

3 测试函数仿真实验与对比分析

为了验证改进的粒子群算法具有运行速度快，不易陷入局部最优，成功率高等优点，选取由Himmelblau提出的作为benchmark测试算法的权威优化问题做为实例，并通过改进PSO算法及其他文献对该实例的优化作对比。该优化实例模型具体形式如下[4]:

式中，X=(x1，x2，x3，x4，x5)T

本文改进粒子群算法用C++语言在VC++6.0实现[5]，在Athlon 64 X2一内存2G 的DIY 计算机上运行，设定相关初始参数如表1所示，经试验测定。

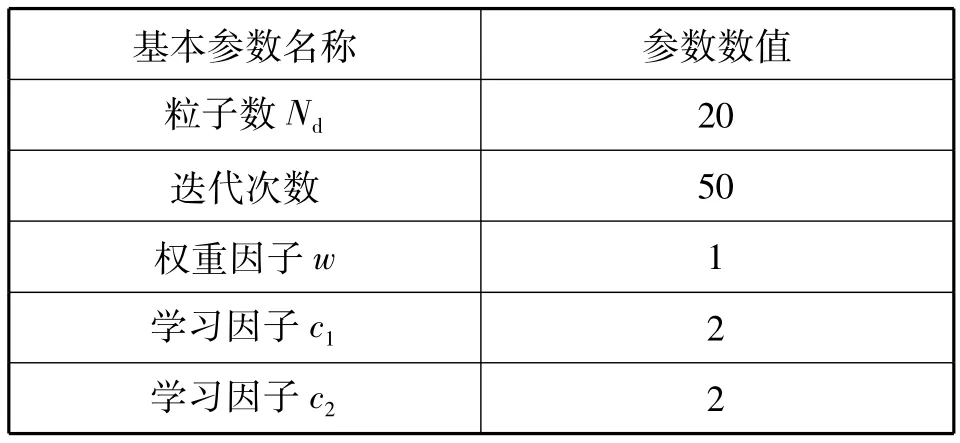
表1 初始参数表Tab.1 Initial parameters

为了更好的反映出每种优化方法的优化性能，和上面文献一样，引成功率指标以及平均有效迭代次数如下[5]:

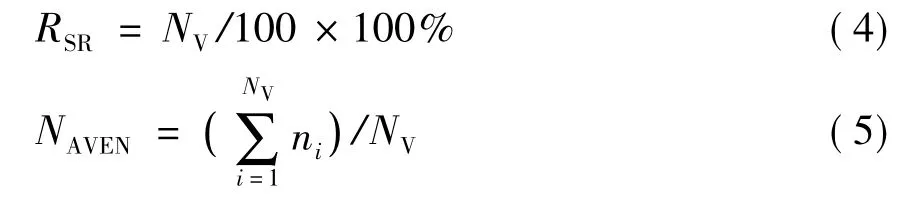
式中的NV表示100次独立试验中能成功获得的最优解的试验次数;ni表示第i次成功获得最优解的迭代次数。根据上述设定参数，对上例进行优化设计，所得结果与文献[6-7]中提供的结果一并列于表2和表3.

从表2中可以明显看出采用APSO算法获得的最优解优于其它方法获得最优解，即精度高;而从成功率来说改进PSO算法成功率为100%，从而验证了理论说明;且平均有效迭代次数也较前面方法降低了数十倍，说明运算收敛速度也最好，即该方法优化效果是很不错的，理想的;运行时间也有特别大的减少，分析原因有两个方面(1):本计算机配置高于文献中配置，(2)APSO算法快速收敛优化也使优化时间降低。

如表3所示，在满足约束条件情况下，采用本文APSO算法，随机进行20次寻优，得目标函数的最优值，该结果比文献中所列结果都好，证明了本文方法可行求解精度高，求解效果优。

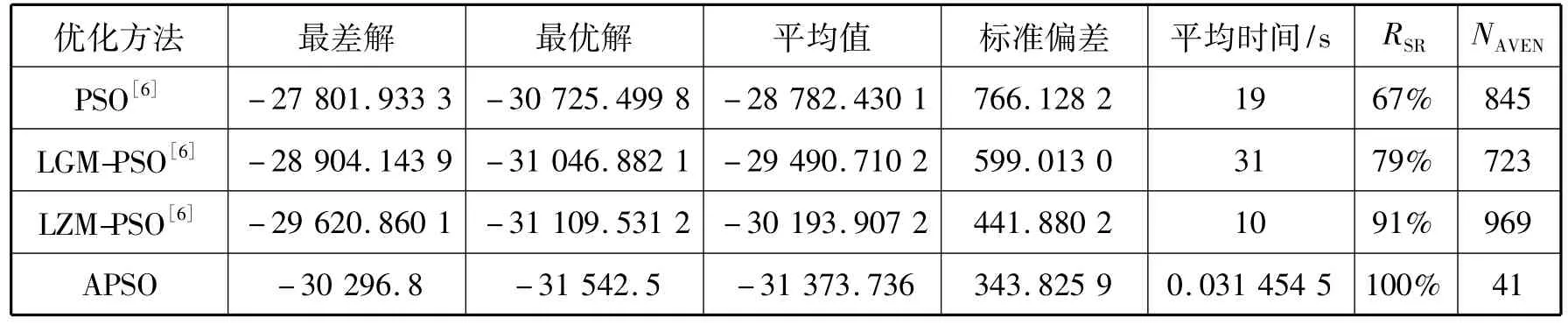
表2 4种优化算法优化结果的对比Tab.2 Comparison of optimization result from 4 optimization algorithms

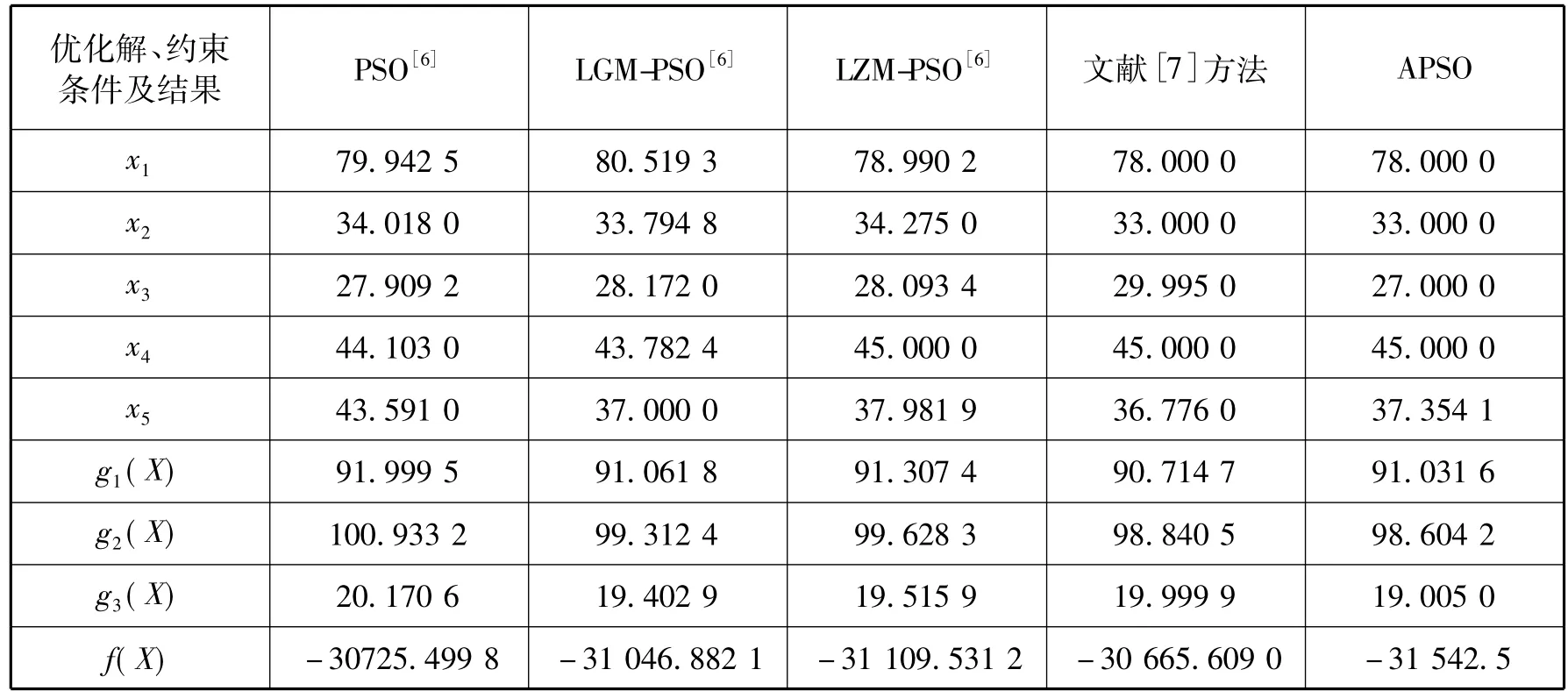
表3 5种优化算法获得的最优结果对比Tab.3 Comparison of optimal solutions from 5 optimization algorithms

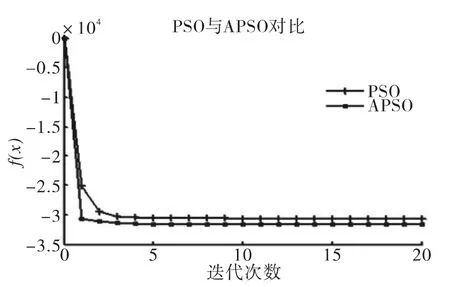
图2 APSO算法的收敛曲线图Fig.2 The convergence graph of PSO and APSO

图2给出了PSO和APSO算法在20次迭代运行时获得最好优化结果时的收敛情况。从图2可以看出。采用改进PSO算法时所优化的结果精确性高，收敛时间早，而且其收敛速度非常快。

4 工程应用算例

为了能够显示出APSO算法在工程应用上的的优点，并研究改进后算法对问题的依赖性，本文选取一个工程有代表性的问题进行优化应用。

4.1 数学模型

单梁起重机广泛应用厂矿企业，其主要结构件主梁截面大多采用箱形截面，截面简图如图3，现对跨度L=22.5 m，额定载重为5 T的起重机主梁截面进行优化，目标是使其质量最轻，并满足主梁的刚度，强度，整体稳定性，局部稳定性以及工艺尺寸等约束[8-11]。优化模型如下:

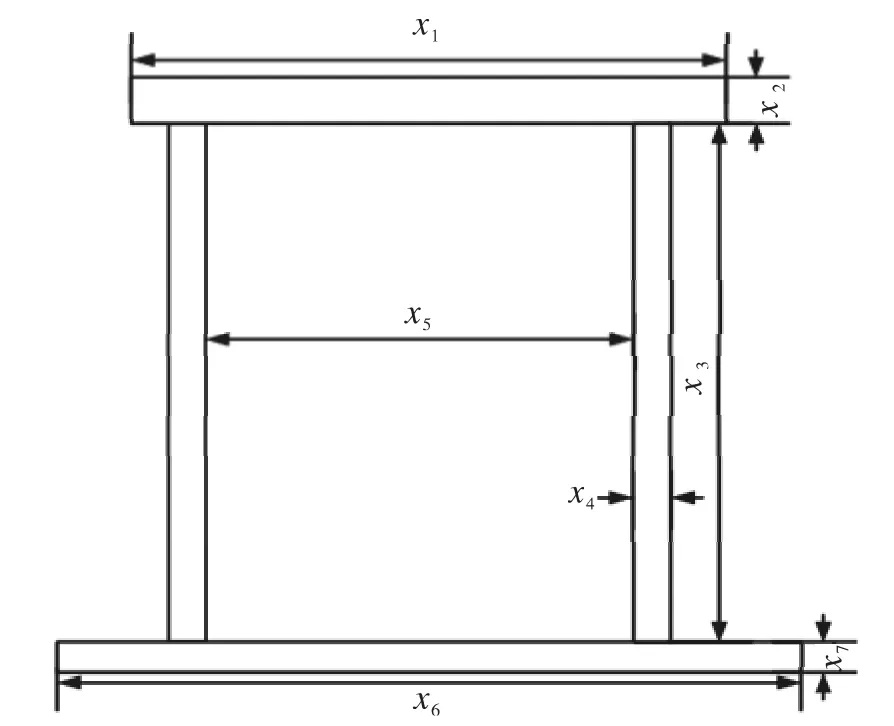
图3 起重机主梁截面结构图Fig.3 The structure figure of girder section

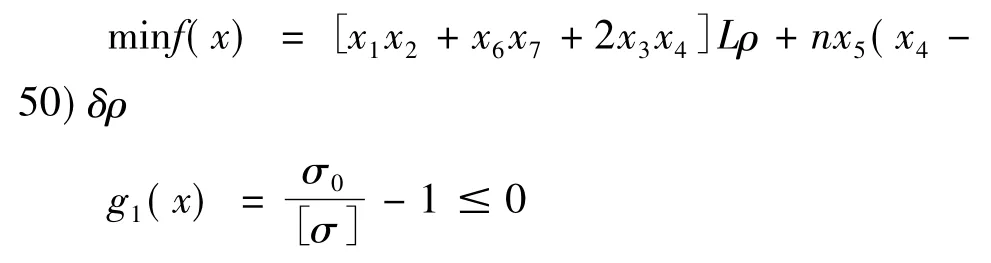
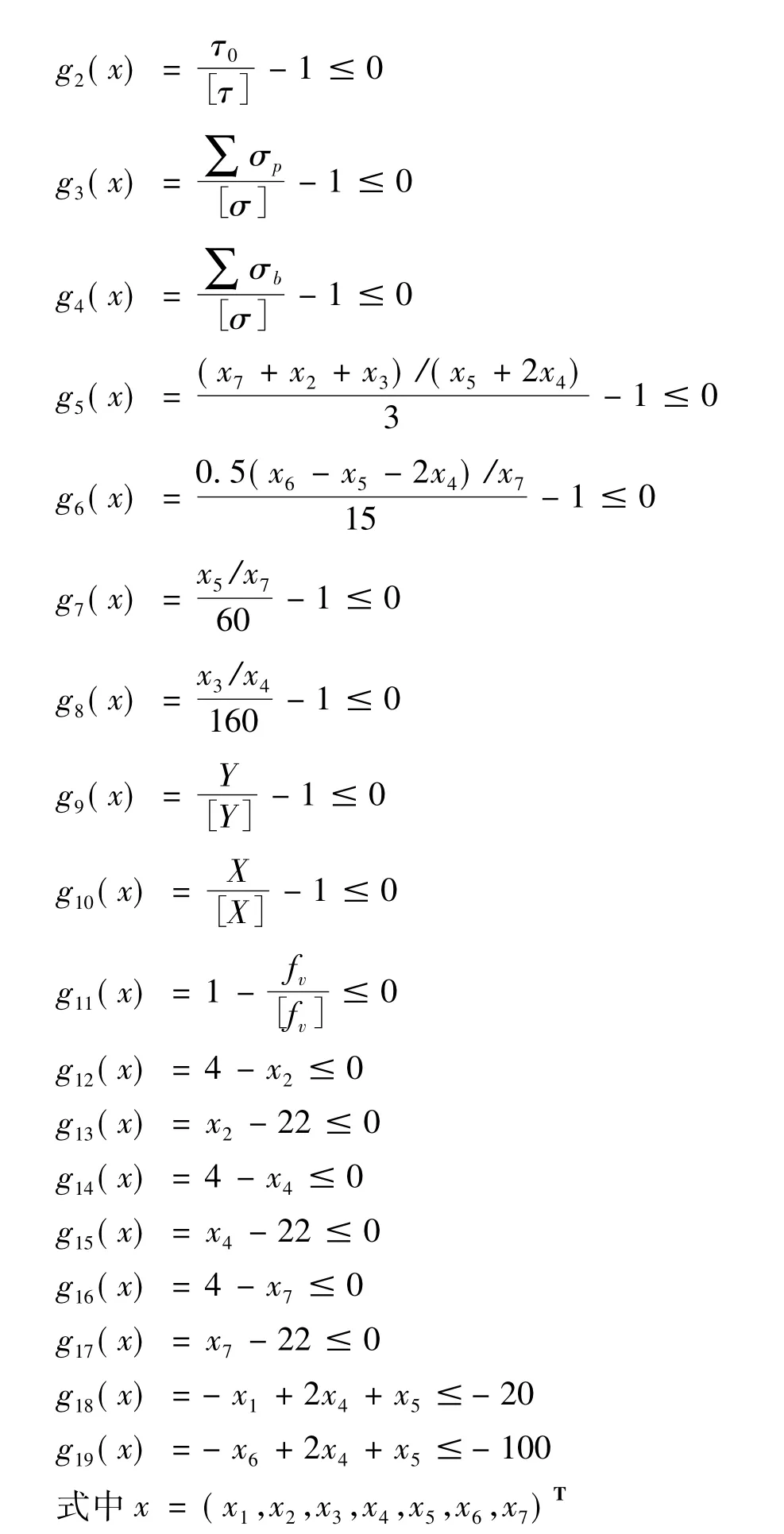
4.2 优化结果分析

为满足工程需要，最优解应为绝对可行域内的解。初始参数取 c1=c2=1.005，w=0.8，最大迭代次数n=100，群粒子数nd=20.对上述实例进行相关截面尺寸参数的优化设计，计算结果与文献[7]中提供的结果一并列于表4.

根据实际生产，对以上优化结果圆整如下:x1=321，x2=11，x3=832.5，x4=5.5，x5=278.5，x6=397.5，x7=21，f(x)=3682.9 ，主梁的质量减轻了近10%，取得比较好的经济效益，特别是梁的高度降低了近40 mm，可以很大的降低厂房的建设成本，并且APSO算法一些方面比MATLAB优化有一定优越性。

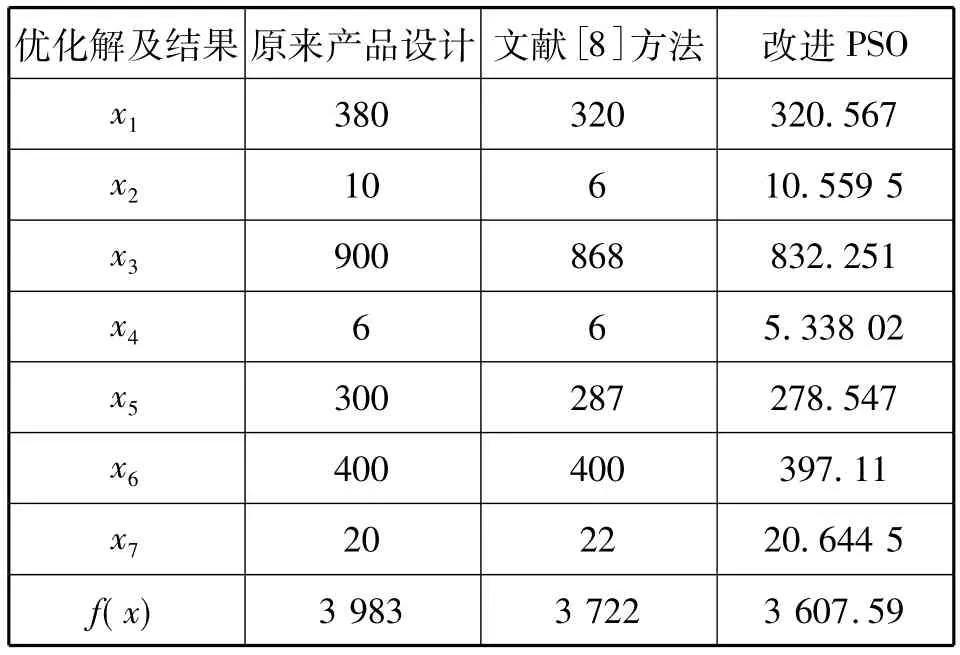
表4 优化结果参数对比表Tab.4 Comparison of optimal solutions

5 结论

(1)通过改进粒子群算法，可以发挥改进后算法的优点，求解工程上非线性约束优化设计问题，其为该类问题的解决提供了新思路。

(2)benchmark测试算法优化设计算例优化结果显示本文方法优于文献中粒子群法、LZM-PSO，LGM-PSO等算法，从而体现出此方法的有效性，用该算法可得到满意的最优解。

(3)主梁结构工程优化设计实例及其工程应用进一步证明了本文方法在求解工程非线性约束优化问题的有效性，且比MATLAB有一定优越性。

[1]KENNEDY J，EBERTHART R C.Particle Swarm Optimization[C]//Proc.IEEE Int’l.Conf.on Neural Networks，1995:l942-1948.

[2]谢晓锋，张文俊，杨之廉.微粒群算法综述[J].控制与决策，2003，18(2):129-133.

[3]曾建潮，介婧，崔志华.微粒群算法[M].北京:科学出版社，2004.

[4]CARLOS A，COELLO C.Use of a Self-adaptive Penalty Approach for Engineering Optimization Problems[J].Computers in Industry，2000，41(2):113-127.

[5]陶元芳.机械工程软件技术基础[M].北京:机械工业出版社，2010.

[6]刘道华，原思聪，兰洋.混沌映射的粒子群优化方法[J].西安电子科技大学学报，2010，3(4);764-769.

[7]HOMAIFAR A，LAI S H Y，QI X.Constrained Optimization via Genetic Algorithms[J].Computers in Industry，1994，35(4):242-254.

[8]李扬，卫良保.基于VC和MATLAB的单梁起重机优化设计.[J].太原科技大学学报，2012，33(1);26-29.

[9]徐格宁.机械装备金属结构设计[M].北京:机械工业出版社，2009.

[10]孙靖民，梁迎春.机械优化设计[M].北京:机械工业出版社，2002.

[11]全国起重机械标准化委员会.GB/T3811—2008起重机设计规范[S].北京:中国标准出版社，2008.