一种适用于彩色图像的秘密共享方案
刘 丽,王安红,刘文杰,王钢飞
(太原科技大学电子信息工程学院,太原 030024)
秘密共享是现代密码学领域中的一个很重要的分支,它对信息和数据的安全存储、传输以及合法利用都有着十分重要的作用。1979年Shamir提出了(k,n)门限秘密共享方案[1],将一个主秘密拆分成n个子秘密分发给n个不同的参与者保管,只有收集到其中任意k个或k个以上的子秘密才能够恢复出主秘密,而任何少于个参与者的集合都无法得到主秘密。通过这种方式,可以分散责任,保证了秘密信息的安全性。
1994年文献[2]将秘密共享的思想应用于图像领域,提出了一种新的图像秘密共享方案,其基本思想:将原秘密图像S分割成n幅影子图像,分发给n个不同的接收者。
(1)任意的k(k≤n)幅或多于幅影子图像的组合均可以恢复原秘密图像S.
(2)任意(k-1)幅或少于k幅影子图像的组合均不能恢复原秘密图像S.
然而,这一方案的缺点是影子图像的尺寸比原秘密图像大,且恢复出的图像失真。这一缺点的存在违背了图像秘密共享方案的初衷,对秘密数据的存储、传输及利用都带来了很大的阻碍。因此,图像秘密共享要求图像质量得到保证的前提下,影子图像尺寸越小越好。
基于(k,n)门限方案,文献[3]利用(k-1)阶Lagrange插值多项式对原秘密图像进行共享,将像素的灰度值作为多项式的系数,从而使得影子图像的大小变为原图像的1/k,且恢复的效果更好。但是由于相邻像素之间存在强相关性,导致生成的影子图像中存在少许的暗影轮廓,甚至在重构时少于个接收者也可能恢复原秘密图像。文献[4]在文献[3]的基础上,引入了Huffman压缩编码,进一步减小了影子图像的尺寸。文献[5]针对图像秘密共享前需要置乱的问题,提出了一种免置乱的秘密共享方案,即保证了影子图像的尺寸为原图像的1/k,也有效降低了算法的复杂度。为了进一步提高算法的安全性,文献[6-8]提出了安全的可验证的秘密共享方案,这些方案弥补了参与者之间欺骗的安全缺陷,同时又减小了算法的计算量。然而,以上方案均是针对灰度图像进行处理,彩色图像的数据量是灰度图像的3倍。因此,对于数据量庞大的彩色图像,以上方案就不能使用了。
针对以上问题,提出了一种适用于彩色图像的秘密共享方案,首先分析彩色图像的R,G,B三个位平面以便对彩色图像进行压缩,然后利用Shamir的(k,n)门限思想将压缩的彩色图像分为n个影子图像,最后通过收集到的k个不同接收者的影子图像恢复原秘密彩色图像。实验表明所提方案不仅有效地减小了影子图像的尺寸、降低了计算复杂度,而且极大程度减少了相邻像素之间的相关性,提高了原秘密图像的安全性。
1 本文的方案
本文的方案由两个关键部分组成:GSBTC压缩编码和Shamir的(k,n)门限方案。如图1所示。
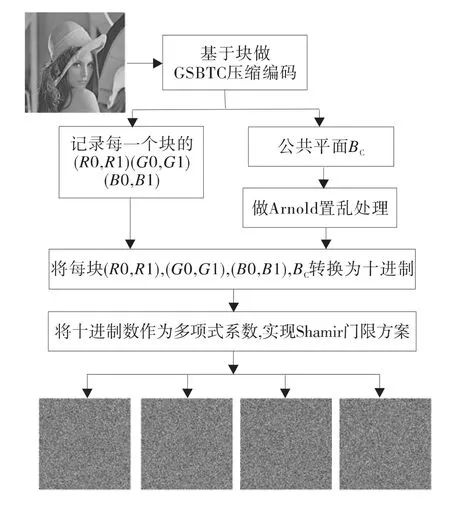
图1 秘密图像共享(2,4)门限方案示意图Fig.1 Sketch map of secret image sharing(2,4)threshold scheme
1.1 GSBTC 压缩编码
在图像秘密共享之前,首先采用GSBTC对彩色图像进行压缩。GSBTC(Gradual search algorithm for one single bitmap BTC)[9],即单一位平面的逐级搜索算法,该算法基于传统的BTC(Block Truncation Coding)编码算法,针对彩色图像的三基色分量,分别确定各分量的位平面,并采用逐位比较的方法来确定三基色分量的公共平面,从而达到压缩的目的。具体步骤如下:
步骤1:将原秘密彩色图像S分成4×4大小且无重叠的块,提取各块的R,G,B三基色分量,对每一个分量作传统的BTC编码,记录每一个分量中0组和1 组像素的均值,即(R0,R1),(G0,G1),(B0.B1),以及每一个分量的位平面 BR,BG,BB.
步骤2:公共平面BC的确定(该步骤基于图像块完成)。
(1)对比 BR,BG,BB这三个平面,若相应位置的值相等,则将该值放入公共平面BC的相应位置中;若不相等,则公共平面BC中相应位置处置空值,即:

其中ri为图像块中第i个像素R分量在BTC编码后的位平面值,gi,bi类似。
(2)使用公式(2)和(3)计算公共平面BC的均方误差MSE,BC中空值的部分可忽略不计。

其中,xi=(xRi,xGi,xBi) 为像素值,p,q 分别为BC中0和1的个数。
(3)搜索BC中的第一个空值,分别用BR,BG,BB面中相应位置的值替换,并利用公式(2)和(3)重新计算 MSE,分别记为 newMSER,newMSEG,newMSEB(注意,此时p,q的值会发生变换)。
(4) 比较 newMSER、newMSEG、newMSEB值,选择其中最小值为newMSE,并用该分量位平面中相应位置的值替代公共平面BC中对应位置的空值。
(5)重复步骤(2)-(4),直到块中所有的空值都被替代。
至此,块的公共平面BC被确定。
步骤3:重复步骤1和步骤2,直到原秘密彩色图像S中所有的块均被处理完毕。
记录每一个块的(R0,R1),(G0,G1),(B0,B1)以及公共平面BC.
1.2 影子图像的产生
为了减小相邻像素之间的相关性,提高图像的安全性,本文采取了以下方案:首先对公共平面BC做50次迭代的Arnold置乱处理,将置乱后的矩阵存入矩阵中,然后对 (R0,R1),(G0,G1),(B0,B1)和利用Shamir(k,n)门限方案进行秘密共享,分割出影子图像。
步骤1:将4×4的矩阵E转换为2×8的矩阵E',将矩阵E'按行转换成十进制数(d0,d1);
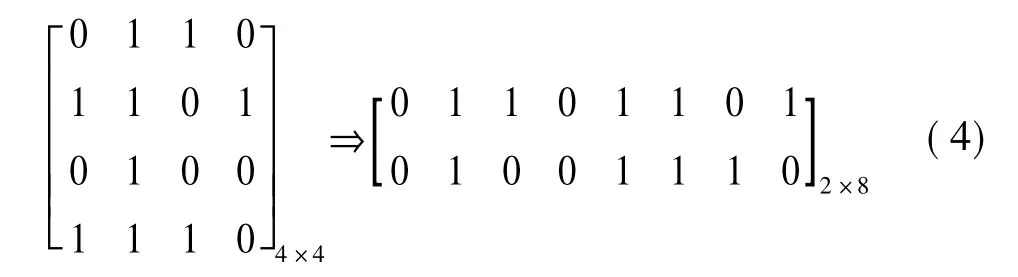
步骤 2:计算每一块的 (R0,R1),(G0,G1),(B0,B1),(d0,d1) 的值,依次放入集合 P 中。
步骤3:从集合P中顺序选取k个未被共享的元素作为公式(5)的k个系数,
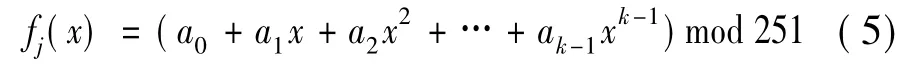
其中 a0,a1,…ak-1是 k 个系数,j∈[1,s],且
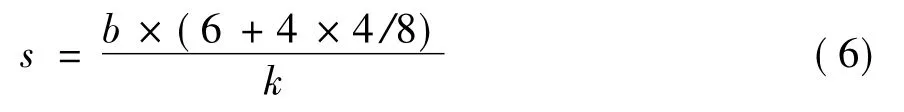
其中,b为原秘密图像的分块数,4×4为分块的尺寸,s为影子图像中像素个数。这里注意,对(R0,R1),(G0,G1),(B0,B1) 分别量化为 2 个字节,而BC占用2字节。
步骤 4:取 x=1,2…n,分别计算出 fj(1),fj(2),…fj(n),并依次顺序赋给幅影子图像矩阵。
步骤5:重复步骤3和步骤4,直到集合P中所有的元素均被处理完毕。将n幅影子图像顺序发给n个接收者。
1.3 图像的重构
在接收端,k个接收者提供合法的影子图像,并通过以下方法重构出原始的秘密图像。
(1)从k幅合法的影子图像矩阵中分别提取出第一个未被处理的像素灰度值,{f1(i1),f1(i2),…,f1(ik)};
(2) 用 k 个点{(i1,f1(i1)),(i2,f1(i2)),…,(ik,f1(ik))}通过拉格朗日插值多项式构造k-1阶多项式,
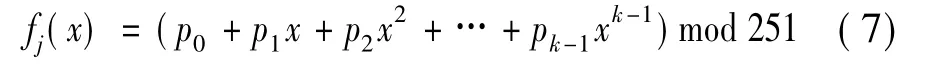
并提取多项式的系数;
(3)重复(1)和(2)直到影子图像中所有的像素点都被处理完毕,依次记录多项式的系数,恢复集合P.
(4)将(d0,d1)转换为二进制,并恢复为4×4的公共平面矩阵E。
(5)做Arnold置乱的逆处理,恢复块的公共位平面BC.
(6)用 (R0,R1),(G0,G1),(B0,B1) 和 BC做BTC的解码,得到原秘密彩色图像S.
2 实验结果与性能分析
根据本文方案,使用Matlab7.0环境做了以下两组实验。
实验一:选取尺寸为512×512的Lena.bmp作为原秘密彩色图像 S,实现(2,4)门限分割方案。如图2所示。

图2 (2,4)门限方案Fig 2 (2,4)threshold scheme
图2中,(a)为原秘密彩色图像S;(b)是由4幅影子图像中第一和第三幅图像组合恢复后的秘密彩色图像,其峰值信噪比PSNR=30.1dB;(c)-(f)为4幅影子图像,其尺寸为256×256,是原秘密彩色图像的1/4.
从图2可以看出,本方案分割后的影子图像没有了原彩色图像的色彩、轮廓和暗影。GSBTC压缩编码属有损压缩,但是恢复后的彩色图像的PSNR=30.1dB.可见,本方案在保证原秘密彩色图像质量的前提下,将影子图像的尺寸缩减到原图像的1/4,同时,在信道中传输的影子图像的数据量是原秘密图像的1/2(每幅影子图像仅需要传输彩色图像块的(R0,R1),(G0,G1),(B0,B1)和 BC的部分信息,分别对应2字节的量化比特,因此数据量是彩色图像的1/6k)。
实验二:选取尺寸为512×512像素的baboon.bmp作为原秘密彩色图像S,实现(8,10)门限分割方案。如图3所示。

图3 (8,10)门限方案Fig 3 (8,10)threshold scheme
图3中,(a)是原秘密彩色图像S;(b)是由8幅影子图像:(c)、(d)、(f)、(g)、(h)、(j)、(k)和(l)组合恢复的秘密彩色图像,其PSNR=22.8dB;(c)-(l)为10幅影子图像,影子图像的尺寸为128×128,是原秘密彩色图像的1/16.
实验二进一步验证了本方案的可行性。由图3可以得出,恢复后彩色图像的质量并未受到很大的影响,影子图像的尺寸缩减到原图的1/16,而在信道中传输的影子图像的数据量是原秘密图像的1/48.
影子图像产生的过程中,方程(6)中的k值越大,相应的s个数就越少,影子图像的尺寸也就越小。可见,影子图像的数量越多,图像的尺寸就会越小,用于信道中传输的影子图像的数据量也就越小。
为了进一步说明实验结论的正确性,本文在相同的环境下对不同尺寸的图像做了大量的实验,实验结果如表1所示。

表1 Shamir门限方案产生的影子图像尺寸对照表Tab.1 The size of shadow image produced by Shamir threshold scheme
表中,T表示原始秘密图像的尺寸(像素点),k表示Shamir门限方案中的门限值。为了使产生的影子图像整齐,k通常取2的整数次幂。通过表1中的数据可以看出,影子图像的尺寸仅为原图像的1/2k大小,明显小于原秘密图像,而送入信道中传输的影子图像的数据量也仅为原秘密图像的1/6k.
3 结束语
本文提出了一种有效的适用于彩色图像的秘密共享方案。彩色图像恢复时,只要任何k幅影子图像即可恢复原秘密彩色图像,而任何少于k幅的影子图像则无法得到关于原图像的任何信息。通过大量的实验数据表明,影子图像的尺寸仅为原图像的1/2k,且送入信道中传输的影子图像的数据量也仅为原秘密图像的1/6k.因此,在实际的应用中,本文方案不仅能大量节省图像的存储空间,同时也能缩减图像的传输时间。然而,由于GSBTC压缩算法属于有损压缩,在对图像精度要求较高的医疗或军事领域内,该方案就不能适用了。
[1]SHAMIR A.How to Share a Secret[J].Communications of ACM,1979,24(11):612-613.
[2]NAOR M,SHAMIR A.Visual Cryptography[C]//Proc.Of Advances in Ctyptology-EUROCRYPT`94.Berlin,Germany:Springer,1995:1-12.
[3]THIEN C,LIN J.Secret Image Sharing[J].Computer Graphics,2002,26(1):765-770.
[4]WANG R Z,SU C H.Secret Image sharing with smaller shadow images[J].Pattern Recognition Letters,2006,27(6):551-555.
[5]周清雷,郭锐.高效免置乱的图像秘密共享方案[J].计算机工程,2010,36(9):126-128.
[6]白晓,余梅生.基于证书的可验证多秘密共享方案[J].计算机工程与应用,2009,45(7):127-128.
[7]候整风,韩江洪.防欺骗(t,n)秘密共享模式研究[J].浙江大学学报:理学版,2007,34(6):633-635.
[8]LI B.A reliable(k,n)image sharing scheme[C]//Proc.Of DASC`06.Indianapolis,USA:2006:31-36.
[9]CHANG C C,WU M N.An algorithm for color image compression based on common bit map block truncation coding[C]//Joint Conference on Information Sciences,2002:964-967.

