基于最优化理论的机步师联合火力打击目标价值评估＊

邹 进 许劲松

（73131部队 漳州 363113）

1 引言

机步师兵种专业比较齐全，结构比较合理，具有先进的信息力、较强的火力、快速的机动力和一定的装甲防护力，是未来遂行城市进攻战斗的主要突击力量［1］。未来城市作战，战场环境复杂多变，战场目标纷繁多样，联合火力打击受制因素多，且重要程度不同，为定量分析、定性判断带来困难［2～3］。本文从最优化的角度给出一种决策方法对目标选取的重点、先后问题进行量化分析，能够有效解决联合火力打击目标的难点问题，为打击目标决策提供新的思路和方法。

2 基于最优化解法的目标价值分析

2.1 最优化解法的基本原理［4～6］

设多属性决策问题有m个目标M1，M2，…，Mn和n个指标A1，A2，…，An，设目标 Mi（i＝1，2，…，m）在指标Aj（j＝1，2，…，n）下的属性值为aij（为确定的数），从而构成决策矩阵A＝（aij）m×n，目标指标属性权重向量w＝（w1，w2，…，wn）未知。然后将决策矩阵A＝（aij）m×n转化为规范化矩阵R＝（rij）m×n，其方法如下

当目标的指标属性值属于收益性指标时：

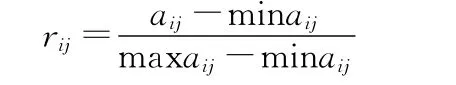
当目标的指标属性值属于损失性指标时：

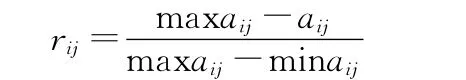
显然，规范化决策矩阵R中rij取值范围为［0，1］，且对应于偏好最高的属性值有rij＝1，对应于偏好最低的属性值有rij＝0。设Y＊为目标价值排序的理想方案，则有Y＊＝（1，1，…，1）∈Rm。

设规范化决策矩阵为R，记

则di（w）反映了方案Ai与理想方案A＊间的距离，显然di（w）越小越好。为了使方案从总体上接近最佳状态，我们应选择权重向量w＝（w1，w2，…，wn），使得每个di（w）都尽可能小。由于每个方案都是非劣的（若存在劣方案则可事先删除），不存在任何偏好关系。因此，可建立下列单目标决策模型mode：

求解此模型，得到最优解w＊＝（w＊1，w＊2，…，w＊m）及相应的值，按di（w＊）的值从小到大的顺序排列即得到方案Ai（i＝1，2，…，m）的优劣排序。

综上所述，此种决策矩阵目标价值排序方法的具体步骤如下

1）根据目标的指标属性构造决策矩阵A＝（aij）m×n，并将其规范化进而得到规范化决策矩阵R＝（rij）m×n；

2）在属性权重w＝（w1，w2，…，wn）（未知）的作用下，建立单目标决策模型。

3）求出单目标决策模型最优解w＊＝（w＊1，w＊2，…，w＊m）及相应的di（w＊）（i＝1，2，…，m）值；

4）按di（w＊）（i＝1，2，…，m）值的从小到大的顺序排列即得到方案Ai（i＝1，2，…，m）的优劣排序。

模型具体解法如下

作拉格朗日（Lagrange）函数：

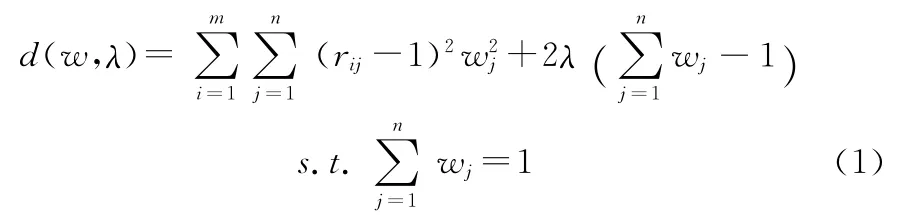
求其偏导数，并令其为0。

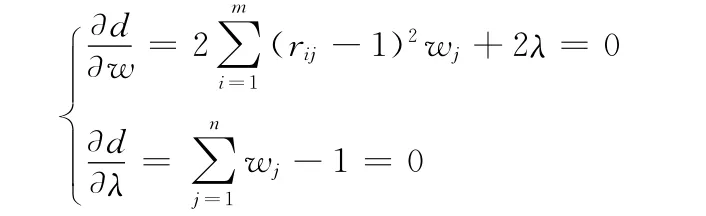
得到：

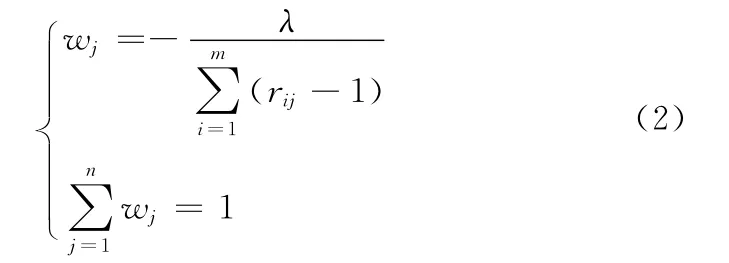
则得：

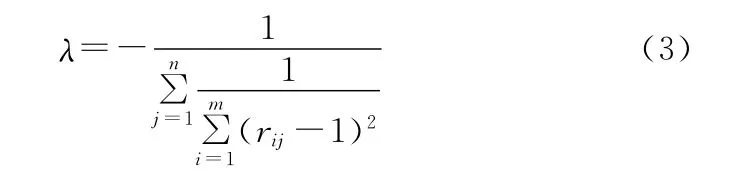
由式（2）和式（3）得：

即求得wj的最优值w＊，然后通过计算di（w＊）就可以进行决策方案的排序，也就得到了目标价值的大小顺序。

2.2 确定目标价值指标和指标评分标准

本文在比较以往各种价值指标体系的基础上，结合信息化条件下联合火力打击的特点，着重考虑了任务一致性、目标重要性、打击紧迫性、情报可靠性、目标易毁性五个对目标价值影响较大的因素，作为衡量目标价值大小的主要指标［7］。

w1（任务一致性）：主要考虑目标对本级作战任务的一致程度。其确定依赖于战场上的敌我双方态势，同一目标在不同的战斗时节对战场的影响不同，应以联合作战中的总体意图为准备。

w2（目标重要性）：主要考虑目标在敌城市整体防御体系中的地位作用。

w3（打击紧迫性）：打击紧迫性要求火力打击单元必须在有限的“攻击窗口”或“打击时机”内发现、识别、定位、攻击目标和评估毁伤情况。未来城市进攻战斗中，机步师联合火力打击的众多目标对时间的敏感性将随战场态势不断发展变化。

w4（情报可靠性）：主要考虑联合火力打击目标的坐标、幅员、数量、性质等信息的准确程度。

w5（目标易毁性）：主要考虑目标受火力打击时被毁伤的难易程度。

3 实例分析

根据战术情况设定和双方编制装备、兵力部署情况，未来城市战斗机步师当面之敌目标主要区分为以下八类：1）指挥所、观察所；2）交通要道；3）情报和通信枢纽；4）炮兵防空兵阵地、导弹阵地、火力点；5）集结的坦克、装甲目标；6）主要防御部（分）队；7）市政机构；8）各类预备队［8］。

对上述八类目标分别命名为 M1、M2、M3、M4、M5、M6、M7、M8，将对敌目标是否优先打击需要考虑的因素划分为任务一致性、目标重要性、打击紧迫性、情报可靠性、目标易毁性等五个因素，即判定因素集为U＝｛M1，M2，…，M8｝，判定因素的指标集为W＝｛w1，w2，…，w5｝。通过指挥员、参谋人员和专家的评分，得到目标的评价信息见表1。其中任务一致性取越接近固定值7越好，目标重要性、打击紧迫性和情报可靠性为收益性指标，目标易毁性为损失性指标［9，11］。

表1 目标价值评分表

具体计算步骤如下：

1）根据表1中数据，从而得到原始数据矩阵A

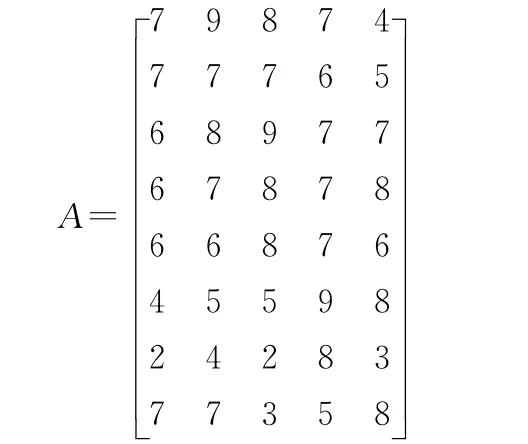
用极差变换法将原始数据矩阵A作标准化处理，得到标准化矩阵R

2）根据式（1），在属性权重未知的条件下，建立单目标规划模型model：

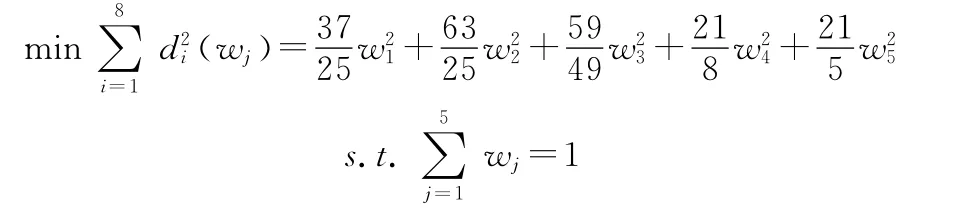
3）由式（4），求得model 1的最优解为

则d1（w＊）＝0.0868，d2（w＊）＝0.1657，

按di（w＊）的值由小到大排列即可得到目标价值顺序为：M1＜M3＜M5＜M4＜M2＜M6＜M8＜M7，即该作战条件下联合火力打击的顺序为：指挥所、观察所，情报和通信枢纽，集结的坦克、装甲目标，炮兵防空兵阵地、导弹阵地、火力点，交通要道，主要防御部（分）队，各类预备队，市政机构。结果较为合理、客观，能够为指挥员科学、合理地实施火力打击提供数据支持。

4 结语

本文深刻分析了影响机步师城市战斗联合火力打击目标选择的各种因素及指标，运用最优化理论和相关性分析，得到比较科学、合理的指标体系，并利用最优化解法计算各指标的重要程度，归一化处理得到指标权重，它既包含了试验所获得的实际数据信息，又考虑到了参谋人员的经验和专家的意见，因此该方法更客观、更科学。并且当指标增加时，在处理数据、进行有效决策方面更具优势，可很快得到结果，为作战指挥提供科学决策支持。该模型不仅可应用于目标选择上，在武器系统效能评估等其他军事问题中也可得到广泛应用。

［1］杜文龙，石利民.联合作战基本力量运用与协同［M］.北京：解放军出版社，2010.

［2］任富兴，赵天翔.信息化条件下炮兵作战研究［M］.北京：解放军出版社，2008.

［3］元书俊，叶艾.21世纪中期的中国炮兵［M］.北京：军事谊文出版社，2007.

［4］刘家学，陈世国.基于主成分分析的投资决策［J］.运筹与管理，2006.

［5］范金城，梅长林.数据分析［M］.北京：科学出版社，2005.

［6］任富兴，王雪琴.现代炮兵计算理论语方法［M］.北京：解放军出版社，2002.

［7］张鹏，陈军.基于模糊综合评判的联合火力打击多目标火力分配优化分析［J］.舰船电子工程，2009（1）.

［8］杨华峰.项目评估［M］.北京：科学出版社，2008.

［9］李义文，王志伟.基于灰色关联分析的炮兵火力打击目标价值评估［J］.四川兵工学，2011（1）.

［10］李明，曲长征，张波，等.基于排队论的战术装备维修力量分配问题研究［J］.计算机与数字工程，2011，39（2）.

［11］刘怡昕，解文欣.炮兵作战指挥理论［M］.北京：海潮出版社，2008.