数字化炮兵侦察情报系统战斗部署方案评价模型*
赵 亮
(陆军军官学院 合肥 230031)
1 引言
数字化炮兵侦察情报系统战斗部署方案的形成是以备选方案形式出现的,因此,对数字战斗部署方案的评价实际上是对所形成方案的综合评价。
2 方案评价指标体系
评价数字化炮兵侦察情报系统战斗部署方案的指标是个多指标的体系,该指标体系能从各个不同的方面反映各个战斗部署方案的综合价值。一套战斗部署方案的优与劣是多指标综合评价的结果,它不能只追求单指标的满意程度。其具体内容包括以下几个指标,见图1所示。
1)任务区分指标
任务区分,就是将建制和配属的力量进行统一的分配,并明确其指挥关系。侦察情报系统任务区分的目的就是通过对建制和配属的侦察力量的统一分配,实现科学合理地使用侦察力量,对敌形成侦察优势,建立全面而有重点的侦察部署,保证侦察力量之间密切配合,顺利完成侦察任务。
2)战斗编组指标
战斗编组,就是按照一定的要求将所属部队、分队和人员进行临时性的组合。侦察情报系统的战斗编组,是指按各侦察单元作战能力和侦察任务需求,以信息网络为媒介,将各侦察单元进行临时性组合的模块编组。其本质是将侦察力量优化组合,形成“合力”,以小型化、标准化、通用化、功能化、动态化的模块进行编组,从而发挥侦察情报系统的最大作战效能。
3)队形配置指标
队形配置,就是作战时根据任务、敌情和地形,将兵力兵器布置在适当的位置。侦察情报系统的队形配置,是指利用战术互联网和情报传输专用网络,使在地理空间上分散的侦察力量连接成一个高效的协调统一体,通过快速机动,形成近、中、远相结合,空中、地面相结合的立体侦察配系。
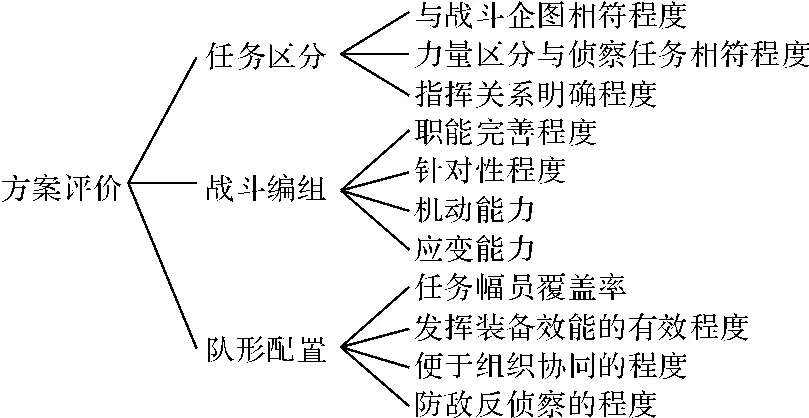
图1 评价指标体系
3 方案评价方法的选择
侦察情报系统战斗部署方案的评价是一个复杂的系统评价问题,解决评价问题的关键是找到一个合适的评价方法,此方法要能反映出问题的本质,并且便于评价的实施。科学的评价方法是方案评价质量的重要保证。常用的评价方法有Delphi法,层次分析法(Analytic Hierarchy Process-AHP)、模糊评判、灰色系统分析法等。
下面简介本文中所用的评价方法。
1)Delphi法。Delphi法是专家会议预测方法的一种发展。概括的说,Delphi法是采用调查方式就评价的问题分别向有关领域的专家提问,而后将他们回答的意见综合、整理、归纳,并反馈给各个专家,再次征求意见,然后再加以综合、反馈。这样经过多次反复循环(一般为三轮),而后得到一个比较一致且可靠性也较大的意见。Delphi法是一种重要的评价工具,“是目前应用最广泛的科技评价方法之一”。它的主要优点是反馈性和统计特性。由于数字化炮兵侦察情报系统的战斗部署方案多是抽象的定性信息,因此,在评价的时候采取相关专家打分的办法是一种比较科学和实用的评价方法。
2)层次分析法。层次分析法(AHP)是决策分析中的一种重要的分析方法,在国防系统分析中有着广泛的应用。美国运筹学家T.L.萨蒂(T.L.Saaty)教授于1980年发表了专著《层次分析法》,书中全面系统地论述了层次分析法的基本原理、应用方法及数学基础。层次分析法是一种定性分析和定量分析相结合的多目标决策分析方法,它将决策者经验判断进行量化,特别适用于目标结构复杂且缺乏必要数据的决策分析问题。

图2 AHP方法递阶层次结构
其基本思路是:首先找出决策问题所牵连的主要因素,将这些因素按目标、准则、措施(方案、手段)等分类;其次,构造一个反映各因素关联隶属关系的递阶层次模型;然后通过每一层各因素之间对上层因素影响的两两成对比较,得到各因素相对重要性排序;最后按照层次结构关系,得到对被选方案的综合排序。其递阶层次结构如图2所示。
注:A为目标层;B为准则层;C为方案层。
层次分析法是一种定性与定量相结合、分为不同层次的多目标、多判据的评价方法,它是定性与定量相结合的方法,且评价的操作实施方便明了。由于本文所论述的问题的层级结构比较清晰,而且需结合定量分析,所以采用层次分析法。另外,由于战斗部署方案的评价不是具体的技术数据,而需要各方面的专家来讨论获取数据,因此,我们在这里选择Delphi法与层次分析法相结合来对数字化炮兵侦察情报系统的战斗部署方案进行评价。
4 方案总体评价
1)找出决策问题相关主要因素,将这些因素按目标、准则、子准则和方案分类并构造一个反映各因素关联隶属关系的递阶层次模型。如图3所示。
对于数字化炮兵侦察情报系统战斗部署方案的评价有目标层:选择最优战斗部署方案。准则层包括两层:准则层和子准则层;准则层包括任务区分指标、战斗编组指标和队形配置指标三个准则要素。子准则层包括:任务区分指标的与战斗企图相符程度、力量区分与侦察任务相符程度和指挥关系明确程度三个子准则要素;战斗编组指标的职能完善程度、针对性程度、机动能力、应变能力和四个子准则要素;队形配置指标的任务幅员覆盖率、发挥装备效能的有效程度、便于组织协同的程度和防敌反侦察的程度四个子准则要素。方案层是n个数字化炮兵侦察情报系统的战斗部署方案,本文设想为三个。
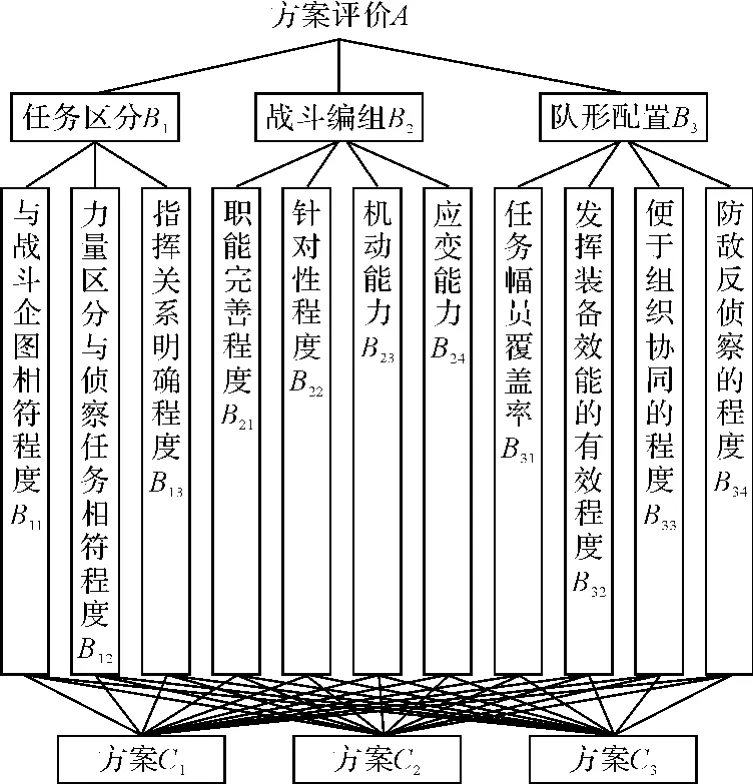
图3 战斗部署方案的评价指标层次结构
2)构造两两比较判断矩阵并对各判断矩阵进行一致性检验。
将每一层次的各因素依次作为准则,对与其关联的下一层次的所有因素进行两两相对重要性比较,相对重要性以重要性标度值来表示,我们这里用最常用的重要性九标度值来表示。如表1所示。

表1 1~9标度法
对于任一准则,与其关联的下一层因素两两比较产生的相对重要性标度值可构成两两比较判断矩阵M(aij),其元素aij为因素i与因素j相同性标度值。我们可得到一系列判断矩阵:
(1)各准则(B1,B2,B3)对侦察情报系统最佳战斗部署方案A重要性的两两比较判断矩阵;
(2)准则B1各子准则(B11,B12,B13)关于B1的重要性的两两比较判断矩阵;
(3)准则B2各子准则(B21,B22,B23,B24)关于B2的重要性的两两比较判断矩阵;
(4)准则B3各子准则(B31,B32,B33,B34)关于B3的重要性的两两比较判断矩阵;
(5)各方案(C1,C2,C3)关于各子准则(B11,B12,B13,B21,B22,B23,B24,B31,B32,B33,B34)的重要性两两比较判断矩阵。
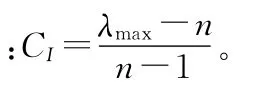
当CI≤0.1时,即可认为判断矩阵基本满足一致性要求。如果判断矩阵的一致性还难以得到满足,可用随机一致性指标RI,RI的求取:先从1/9,1/8,…,1,2,…,9等标度值中随机抽出一个构成n维判断矩阵的一个元素,用同样方法获得判断矩阵的所有元素,再按一致性指标公式求得一致性指标。按上述过程重复多次,即可得到一系列的一致性指标值,取这些值的平均值即是n维判断矩阵的随机一致性指标值RI。表2给出了随机一致性指标值RI随n变化的情况。

表2 随机一致性指标值的变化
然后,我们可以用一致性指标比CR来检验判断矩阵的一致性,其中CR由下式求取:CR=CI/RI,当CR<0.1时,判断矩阵的一致性可以接受,而当CR>0.1时,通常应对判断矩阵进行适当的修改,而后再进行一致性检验,直到判断矩阵的一致性可以接受为止。
3)计算各层因素及方案相对于总目标的组合权重。最后,我们根据各方案相对总目标的组合权重进行排序,便可得出最优战斗部署方案。
[1]任富兴,王雪琴.现代炮兵计算理论与方法[M].北京:解放军出版社,2002:177-183.
[2]陈之宁.模糊数学及其军事应用[M].北京:海潮出版社,2003:84-87.
[3]彭祖赠,孙韫玉.模糊数学及其应用[M].武汉:武汉大学出版社,2002:142-146.
[4]马守华.信息化炮兵作战能力评估问题研究[D].合肥:炮兵学院,2009:24-27.
[5]董明林,李炬.数字化战场[M].北京:星球地图出版社,2009:77-80.
[6]薛向锋,甘明.信息化条件下炮兵侦察力量运用研究[J].合肥:炮兵学院学报,2006(1):26-28.
[7]王建盈.陆军数字化部队作战研究[M].北京:国防大学出版社,2002:86-88.
[8]刘树海,赵天翔.信息化炮兵战斗部署指挥[M].北京:解放军出版社,2004:125-127.

