基于卡尔曼滤波的地形辅助导航＊

周亦军 郑 彤

（海军驻四三八厂军事代表室 武汉 430064）

1 引言

海底地形辅助导航系统［1～7］是近几十年出现的一种新型的导航系统，是水下运动载体导航技术的一个发展方向。利用海底地形进行导航的就是将水下载体实际测量的水深值与已存在的地图进行匹配，对水下载体进行定位，基本原理［1～3］如图1所示。在海底地形辅助导航系统中，精确的数字地图和合适的匹配算法是核心技术，这也是当前相关领域的重点和热点研究问题。

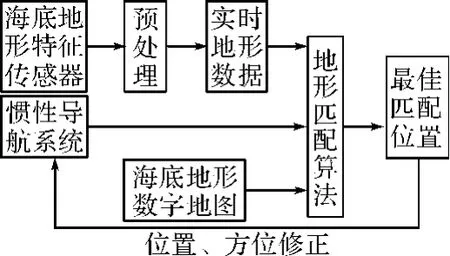
图1 水下地形辅助导航基本原理

文献［8～14］研究了SITAN（Sandia Intertial Terrain－Aided Navigation）算法和TERCOM算法（Terrain Contour Matching）在空中载体中的应用，其在各种地形和不同覆盖层上空均显出了自主、可靠的隐蔽特性。但受INS精度、数字地形图的精度、雷达高度表测量精度和匹配算法的影响较大。近年来使用比较多的是ICCP算法（Iterative Closest Contour Point）［15～21］，它 是 ICP 算 法 （Iterative Closest Point）的一个特例。

多波束测深系统［22］，是在回声测深仪的基础上发展起来的一项海底地形精密勘测技术，是近几十年来海洋测绘界进行海底地形条带式探测的热点。本文利用的海洋测绘多波束测量试验测得的真实地形数据来建立的真实地形数据库，并在此基础上，通过仿真研究水下载体在航行过程中，采用ICCP算法修正惯性导航系统累计误差，提高水下载体的导航精度，为水下载体实现水下、长期、精确导航提供技术支撑。

2 匹配算法

ICCP算法最初来源于图像配准的ICP算法，不需事前确定对应估计，只是不断重复（初始）运动变换—确定最近点—求运动变换的过程，逐步改进运动的估计。算法的主要思路是：将测得的沿着航迹的水深值连接起来构成曲线，与已存在的水深等值线图进行匹配。主要是通过最近点的迭代实现测量图像与模型之间的对准和匹配。算法采用欧氏距离平方最小为目标函数，求得测量航迹与真实航迹之间的最优变换，通过该变换校正航迹，实现对测量航迹的校正，如图2所示。

图2中由Pi（i＝1，2，…，N）点构成的是“指示航迹”，N为航迹点序号。弯曲实线称为“实际航迹”，由Xi（i＝1，2，…，N）构成，Ci（i＝1，2，…，N）表示的是当地实测水深等值线。由于惯导误差的存在，｛Pi：i＝1，…，N｝和｛Xi：i＝1，…，N｝之间必定存在误差。Xi必定位于Ci的等值线上，那么按照一定的准则，使Pi靠拢到Ci上，从而找到最优估计点Yi和对应的“匹配航迹”，实现对真实航迹的最优估计。

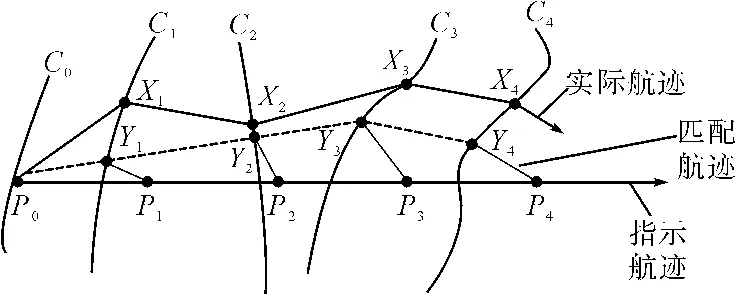
图2 ICCP算法原理示意图

对于ICCP算法的匹配过程可解释为：从已知点p0出发，沿真实航迹航行，并不断测量水深。在实时测深传感器没有测量误差的情况下，这些测量点一定落在对应的等值线上。由于有测量误差，测量航迹给出的位置一定偏离对应等值线。分别设指示航迹位置点集合为｛Pn｝，对应的实际航迹点集合为｛Xn｝，为了求得真实位置，将测量航迹与真实航迹匹配，需要确定刚性变换T（包括一个旋转分量和二个平移分量），通过刚性变换T使集合｛Pn｝与集合｛Xn｝的距离最小。由于集合｛Xn｝一定在等值线上，只是无法确定在等值线上的确切位置，因而在最优化目标函数的基础上采用迭代方法寻找刚性变换T，使式（1）表示的距离最小。

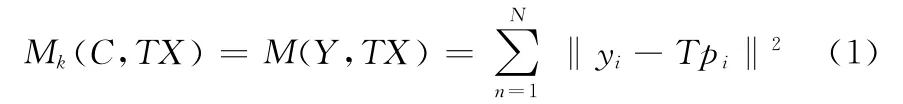
式中，T表示变换，包括旋转和平移。

3 惯导误差方程与卡尔曼滤波

以平台式惯导为例，系统误差状态方程［23～24］为

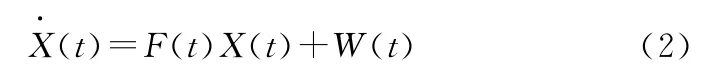
式中 X（t）＝［φx，φy，φz，δVx，δVy，δφ，δλ，ΔAx，ΔAy，εx，εy，εz］为惯性导航系统的12维误差状态矢量，F（t）为状态矩阵；W（t）为12维系统噪声向量；φx，φy，φz，δVx，δVy，δφ，δλ分别为平台误差角、速度和位置误差；ΔAx，ΔAy，εx，εy，εz分别为加速度计误差和陀螺漂移。

在重力辅助惯性导航系统中，由匹配算法得到最佳匹配位置后，利用其与惯导指示位置的误差作为观测量，其量测方程可表示为

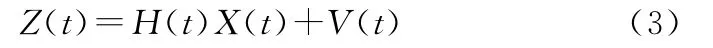
4 获得真实地形数据

进行船测试验，利用多波束测深系统测量真实的地形数据。多波束测深系统是采用发射、接收指向性正交的两组换能器阵获得一系列垂直航向分布的窄波束。如图3所示波束数为16，波束角为2°×2°的单方面换能器多波束系统。图3中系统声信号的发射和接收由方向垂直的发射阵和接收阵组成。发射阵平行船纵向排列，呈两侧堆成向下方发射2°（沿船纵向）×44°（沿船横向）的扇形脉冲声波。接收阵沿船横向排列，但在束控方向上接收方式与发射方式正好相反，以20°（沿船纵向）×2°（沿船横向）的16个接收波束角接收来自海底照射面积为发射2°（沿船纵向）×44°（沿船横向）的扇区回波。接收的回波经过原始的编辑后，使用专业软件CARIS HIPS and SIPS进行处理（如图4所示），就可以得到真实的地形数据了，但为保密起见，本文中涉及的地形图都将经纬度隐去。

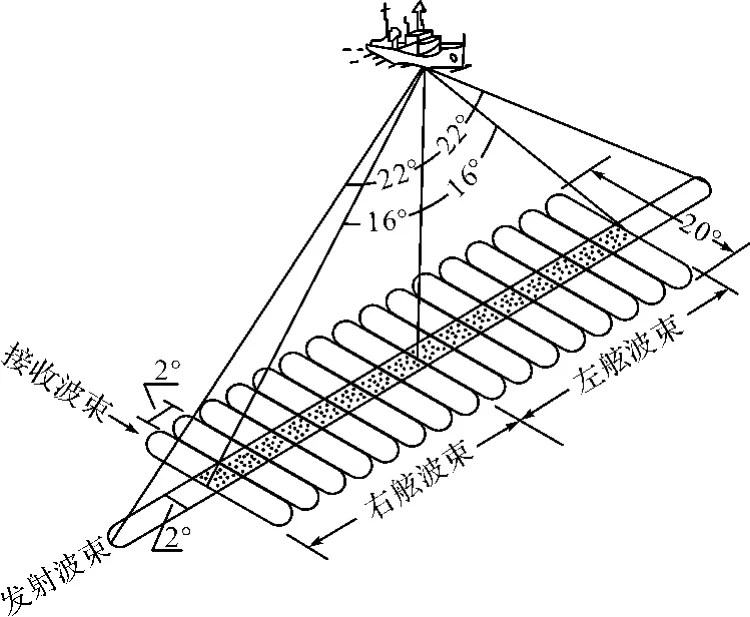
图3 多波束测深系统示意图

5 仿真分析

考虑水下载体以某一航迹航行，水下载体实际航迹为以某一角度自西向东航行。图4所示载体的真实航迹，指示航迹以及匹配航迹。如图所示匹配航迹跟真实航迹形状是一致的，说明将ICCP算法用于水下地形匹配能取得比较满意的匹配结果。然后利用最佳匹配位置对惯导的误差进行修正，以位置误差作为观测量，用卡尔曼滤波对导航系统的误差进行最优估计，将最优误差估计值去校正导航系统。

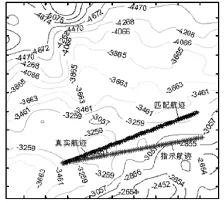
图4 地形匹配辅助导航

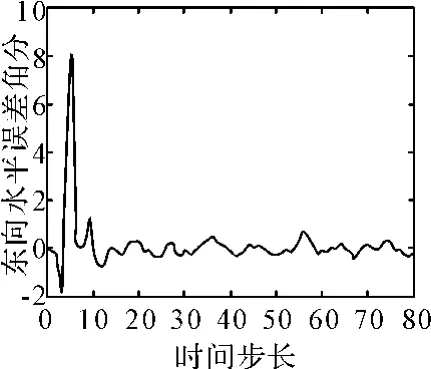
图5 东向水平误差角估计

设系统状态X的初始值X（0）为0，等效陀螺漂移为0.11°／h，加速度计的初始偏差均取为1×10－4g，惯导平台的初始误差角为φx0＝300″、φy0＝300″、φx0＝1500″，惯导初始定位误差在北向及东向均为500m，初始速度误差为1.8m／s，水下潜器航速为8节，考虑到潜器航速、地图分辨率以及航迹采样点数，滤波周期选为250s。在以上仿真条件下得到的惯导各误差估计值如图5～图7所示。

图5、图6为平台水平误差角估计，图7为方位误差角估计，三种误差的最终收敛值如表1所示。由图和表可以看出：用ICCP算法计算出的匹配位置误差作为量测值进行卡尔曼滤波，可有效估计惯性导航系统的误差，进而惯导系统的速度、位置、平台误差角都能很好地被修正。

图6 北向水平误差角估计

图7 水平误差角估计

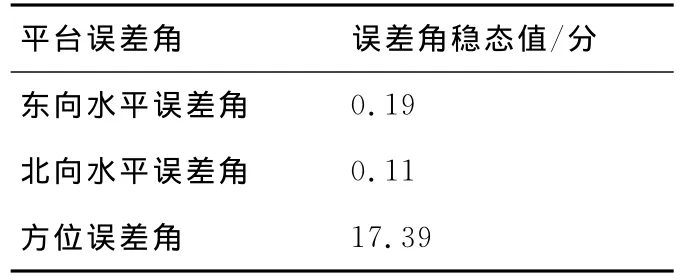
表1 平台误差角稳态值

6 结语

地形辅助导航是导航技术研究的一个新方向，该技术具有诸多优点。本文采用的是ICCP算法作为数据处理的主要方法。并利用多波束测深系统测得的真实地形数据，建立的地形数据库，在此基础上，用该算法进行了仿真计算，并得到了比较满意的匹配结果。该算法的主要优点在于它不需要对数字地图的数据做预处理或进行特征提取等操作，算法原理简单。为了进一步验证所得匹配位置是否适合用来修正惯导的积累误差，将匹配位置误差作为观测量，用卡尔曼滤波对惯导系统误差进行最优估计，由最后的仿真结果可以看出，以匹配位置误差作为观测量可较好的估计惯导系统各项误差。

［1］王英钧.地形辅助导航综述［J］.航空电子技术，1998（1）：24－29.

［2］L.Lucido，B.P.Popesque，J.Opderbecke，et al.Segmentation of Bathymetric Profiles and Terrian Matching for Underwater Vehicle Navigation［J］.Internation Journal of Systems Science，1998，29（10）：1157－1176.

［3］刘光军，袁书明，黄咏梅.海底地形匹配技术研究［J］.中国惯性学报，1999（1）：19－22.

［4］吴凤德.美国战略潜艇导航的现行技术和新技术综述［M］.吴祖铨译.舰船导航，1999，5.

［5］刘光军，陈晶.海底地形辅助导航系统仿真技术研究［J］.计算机仿真，2000，17（2）：21－24.

［6］张飞舟，侣文芳，晏磊，等.水下无源导航系统仿真匹配算法研究［J］.武汉大学学报信息科学版，2003，28（2）：153－571.

［7］刘准，佀文芳，陈哲.海底地形匹配技术研究［J］.系统仿真学报，2004，16（4）：700－703.

［8］Hollowell J.Heli／SITAN：a terrain referenced navigation algorithm for helicopters［C］／／IEEE Position，Location，and NAVIGATION Symposium 1990（PLANS’90），Las Vegas，NV，USA，March 20－23，1990：616－625.

［9］Pei Y.，Che Z.，Hung J.C.BITAN－II：an improved terrain aided navigation algorithm［J］.IECON Proceeding，1996（3）：1675－1680.

［10］Russell E.，Darryl M.Terrain－aided navigation using the Viterbi algorithm［J］.Joural of Guidance，Control and Dynamics，1995，43（9）：1444－1449.

［11］Feng Q.T.，Shen L.C.，Chang W.S.，et al.An HMM based terrain elevation matching algorithm［J］.Acta Automatica Sinica，2005，31（6）：960－964.

［12］Golden J.P.Terrain contour matching（TERCOM）：a cruise missile guidance aid［C］／／Proceedings of the Society of Photo－Optical Instrumentation Engineers，San Diego，CA，USA，July 20－August 1，1980，238：10－18.

［13］朱华勇，沈林成，常文森.基于地形差分矩的TERCOM地图性能估计［J］.国防科技大学学报，2000，22（4）：98－101.

［14］徐克虎，沈春林.地形辅助惯性导航系统研究［J］.南京航空航天大学学报，1997，29（3）：289－294.

［15］Behzad K.P.，Behrooz K.P.Vehicle localization on gravity maps［J］.Proceedings of SPIE－The International Society for Optical Engineering，1999，3693：182－191.

［16］Maurer C.，Aboutanos G.，Dawant B.，et al.Registration of 3－D image using weighted geometrical features［J］.IEEE Tansactions on Medical Imageing，1996，15（6）：836－849.

［17］Cordon O.，Damas S.Image restration with iterated local search［J］.Journal of Heuristics，2006，12（1－2）：73－94.

［18］Madhavan R.，Hong T.，Messina E.Temporal range registration for unmanned ground and aerial vehicles［C］／／IEEE International Conference on Robotics and Automation，new Orleans，LA，USA，April 26－May 1，2004：3180－3187.

［19］于秋则，程辉，田金文，等.基于等高线图与小波变换的3D地形匹配算法研究［J］.宇航学报，2004，25（3）：262－268.

［20］Madhavan R.，Durrant－Whyte H.F.2Dmap－building and localization in outdoor environments［J］.Journal of Robotic Systems，2005，22（1）：45－63.

［21］Bishop G.C.Gravatational field maps and navigational erros［J］.IEEE Journal of Oceanic Engineering，2002，27（3）：726－737.

［22］刘经南，赵建虎.多波束测深系统的现状和发展趋势［J］.海洋测绘，2002，22（5）：3－6.

［23］董绪荣，张守信，华中春.GPS／INS组合导航定位及其应用［M］.长沙：国防科技大学出版社，1998.

［24］许丽佳，陈阳舟，崔平远.GPS／INS组合导航系统中的信息融合算法研究［J］.计算机仿真，2004，21（5）：20－23.