基于ARPA算法的航海应用研究*
王 斌
(中国人民解放军海军蚌埠士官学校航海教研室 蚌埠 233012)
1 引言
自动雷达标绘仪译自英文Automatic Radar Plotting Aid简称ARPA,亦即“自动避碰系统”是以分析过去的雷达信息为基础,依靠本船行动的变化提前预测出相对运动的变化。目前船舶上大多装备的ARPA是矢量型,即DARPA。它是在目标被录取后,计算机即对其进行自动跟踪,约30s后,在显示屏幕(Plan position indicator-PPI)上以目标所在的位置为起点,出现目标的速度矢量,矢量时间连续可调,既可以显示相对运动速度矢量,也可以显示真运动速度矢量,并能以数字方式显示DCPA、TCPA和目标运动要素,这种类型的显示与传统的标绘方法相似,海员在使用时也较方便[1]。但是D-ARPA存在的不足是:首先,不论变向还是变速避让,必须进行试操纵,操作过程耗时,程序复杂,不直观;其次,屏幕上不能直观显示DCPA、TCPA;另外,不能实时确定避让决策和实时评估和直观显示避让决策的有效性。
本文设计了一种能够直观地为操纵者提供当前态势,通过调整机动船的速度矢量,以可视化的方式为操纵者提供避碰决策依据的雷达避碰算法。
2 自动避碰系统算法[7]
2.1 坐标系统转换算法
坐标系转换算法是进行雷达避碰绘算的基础,用于罗盘坐标系和笛卡尔坐标系转换的算法可以以极坐标作为中介进行坐标转换。现将算法描述如下
1)罗盘坐标转换为极坐标:

2)极坐标转换为笛卡尔坐标(直角坐标):

3)将笛卡尔坐标转换为极坐标:

4)将极坐标转换为罗盘坐标:

2.2 目标运动要素提取算法

表1 目标要素
设:本船要素为:(CT,V),雷达测定来船数据为
1)将雷达测定的来船数据(罗盘坐标)转换为笛卡尔坐标:

2)计算时间区间[T1,T2]内我船速度矢量的反矢量:

式中:Span(T2,T1)为计算时间间隔的函数。
3)绘算来船的运动要素:

2.3 避碰要素绘算算法[4,8]


2)求∠A1′C′B′和∠A2′C′B′


图1 避碰要素绘算图解
3 基于算法的航海应用举例
3.1 系统框架设计[5~6]
在进行相关技术和算法的验证之后,ARPA系统平台采用结构化的程序构建方法,根据相应的功能要求将平台划分为态势绘算模块、避碰绘算模块、显示模块、交互模块和扩展接口模块五个模块进行实现。系统的结构如图2。

图2 拓展ARPA算法系统框架设计
1)交互模块:用于对平台参数进行初始设定、输入初始态势、管理目标信息、设定避碰模式和显示方式。
2)态势绘算模块:用于对由拓展接口模块输入的初始态势进行标绘,对各目标的运动要素和碰撞威胁级别进行计算和标绘,对DCPA和TCPA进行计算和标绘。
3)避碰标绘模块:用于对当前态势下的各目标根据设定的安全圆半径(DCPA0)和标绘时延(Span)进行避碰绘算。
4)显示模块:用于显示当前态势下各目标绘算结果并根据避碰显示设定标绘在舰操图上。
5)拓展接口模块:用于接受界面输入或雷达点迹线性拟合程序的目标初始态势。
3.2 基于上述拓展算法的船舶接近到相遇机动的ARPA实践过程[3]
为了保证本文所设计的算法的可操作性,选取现在船舶普遍使用的RM-1290雷达组合的自动避碰系统进行具体的操作步骤阐述。操作步骤如图3所示。
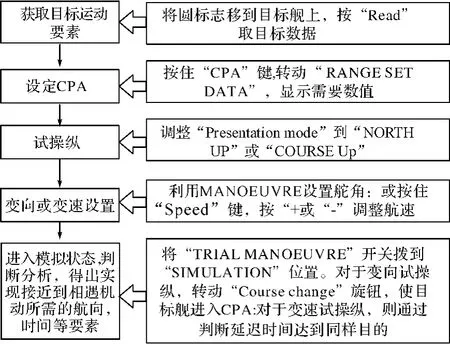
图3 拓展ARPA算法操作过程
4 结语
针对目前船舶大多装备的D-ARPA雷达计算出目标运动矢量操作复杂,不够直观的特点,本文设计了一种操作简单且能够直观地为操纵者提供当前态势,并能实时为操纵者提供避碰决策的雷达避碰算法,对船舶操纵者保证航行安全,有重要意义[2]。
[1]姚洪滨.航海学[M].北京海潮出版社,2001:56-67.
[2]王世远.航海雷达与ARPA[M].大连海事大学出版社,1998:23-24.
[3]石侃.雷达标绘自动化模块算法研究[C]//船舶航泊实践研究论文集,2010:123-126.
[4]熊和金,刘祖源.船舶避碰控制系统模型研究[J].武汉造船,2000,6(3):48.
[5]程启明,马如宏.船舶自动航行系统[J].盐城工学院学报,1999,12(3):67-68.
[6]齐国清,贾欣乐.船舶综合导航系统[J].大连海事大学学报,1998,24(1):31-32.
[7]张文涛,谭毅华,余晋刚.桥区运动船舶的检测和跟踪[J].计算机与数字工程,2011,39(10).
[8]姚杰,吴兆麟,方祥麟.船舶碰撞危险的模糊决策[J].大连水产学院学报,1998,13(2):16.

