基于混沌思想的可多步搜索的新型粒子群优化算法
林博艺
(泉州信息职业技术学院,福建 泉州 362000)
基于混沌思想的可多步搜索的新型粒子群优化算法
林博艺
(泉州信息职业技术学院,福建 泉州 362000)
针对基本PSO算法在全局优化中收敛精度低和易陷入局部极值的不足,提出一种基于混沌思想的多步搜索的新型的粒子群优化算法(CMPSO).该算法先引入混沌思想对粒子种群进行位置初始化,然后再引入多步搜索,最后引入概率条件的选择性重新初始化.通过与其它三个改进算法比较,结果表明CMPSO算法的有效性.
粒子群优化;多步搜索;混沌
1995年Kennedy博士和Eberhart教授提出粒子群优化(Particle Swarm optimization,PSO)算法[1,2],它是一种基于群体智能(Swarm Intelligence,SI)仿生的优化方法,该算法基本思想是源于对鸟群捕食行为的模拟.由于其原理简洁,参数较少,易于实现等优点,成为继遗传算法后的研究热点之一.其已被广泛的应用于函数优化[3],工程优化[4],参数估计[5-9],电力系统优化[10-14],控制器设计[15-7],机器人路径规划[8]等.
类似于GA,PSO算法也有收敛精度低,早熟等不足[18-20],因此继Kennedy和Eberhart之后有许多改进型PSO算法提出.如:引入惯性权重,加入微分演化或是交叉操作,加入混沌初始化,与其它智能算法混合等,这些算法在增加算法得杂度的前提下,都不同程度的提高算法的性能.但这样做都有悖于算法的初衷:简洁实效.本人在分析基本PSO算法不足的基础上,引入混沌初始化,并将多步式位置更新引入其中,并通过实验来验证我们改进的有效性.
1 PSO简介
一个有N个粒子的种群,在D维空间中进行寻优过程的算法的基本递推公式:

其中:i=1,2,…,N;d=1,2,…,D;Xid(k+1),Xid(k),Vid(k+1),Vid(k)分别表示第 i个粒子在 k+1 和 k代的空间位置对应的第d维值及运动速度对应的第d维值;ω为惯性权重;c1,c2分别表示粒子个体和粒子群体的加速权重系数;r1,r2均为0到1之间的随机值,分别表示粒子个体和全体的加速权重;Pid与Pgd分别表示第i个粒子个体在搜索过程中自身的历史最佳位置和整个粒子群体目前找到的最佳位置.
2 新的PSO算法
2.1 PSO算法陷入局部收敛的原因
基本PSO算法易陷入局部极值的原因在文献[3]做了详细的分析,并通过数学推导得到式(3):

由式(3)可知,每个粒子不仅受它自己找到的当前最优解的吸引,而且还受全局最优解的吸引.如果这两个最优解都是局部最优值,粒子将被这两个值吸引而很快重复相同的搜索轨迹.由于式(1)没有使算法跳出局部最优的机制,随着进化迭代的进行,粒子最终将聚集到由个体极值位置P0和全局极值位置Pg共同决定的位置P*上,如果P*是某个局部最优位置,且所有粒子在向位置P*靠拢的过程中若没有找到优于Pg的位置,则基本PSO的进化过程将很难跳出该局部最优,粒子将逐步收敛到P*.另外,结合式(1)还可看出,惯性权重仅能改变粒子的搜索步长,不能改变其运行方向,从而不能克服早熟问题.可见,加强搜索多样性、使算法跳出局部最优,是提高算法收敛速度和寻优精度的重要措施.本文从以下三个方面入手,提出一种基于混沌思想和多步搜索的PSO算法.
2.2 初始化粒子群初始位置
混沌序列的运动特点:随机性和遍历性及规律性.本文采用混沌序列的这一特点对粒子进行初始化分布,这样可以更好的体现初始种群的多样性,为在寻优空间中找到最优解和加快收敛速度奠定较为坚实的基础.
Logistic映射是一个典型的混沌系统,首先利用Logistic映射产生混沌序列,如式(4):

式(4)中 μ 为一个常数,μ∈[3.56,4.0],称为控制参量,主要用来控制系统的混沌程度,L(d)∈(0,1),d=1,2,3,…,D.
第二步对处于D维中间中的N个粒子,首先产生 N 个初始值:L1(1),L2(1),…,Li(1),…,LN(1),把这N个初始值代入式(4)中进行D次迭代运算,将产生的结果代入式(5)中运算:

式(5)中:Xi,d表示第i个粒子第d维坐标,而Li(d)是第i个粒子用Li(1)经过d次迭代运算产生的值,Maxd,Mind分别是第d维的上下限.
2.3 引入多步搜索
由公式(1)知,粒子的运动失量由惯性项Vid(k),自身认知成分项c1*r1*(Pid-Xid(k)),社会认知成分项c2*r2*(Pgd-Xid(k))三项决定的,受人类活动行为的启发可知:人类在做事时,有时会惯性式的执行,有时会加以总结靠自身的经验,有时却也会对所有信息加以汇总考虑然后再去做事(基本PSO算法则是这种方式)[19].本文在尽量不增加PSO算法的基础上,对运算过程中的三项结果直接加以分析迭代:

(6)Xid(k+1)3=Xid(k)ω*Vid(k)+c1*r1*(Pid-Xid(k)) (7)Xid(k+1)2=Xid(k)+ω*Vid(k)Xid(k+1)new=!###"###$Xid(k+1)2 if(f(Xid(k+1)2)) 由式(8)可知,粒子在搜索过程中,先利用自身惯性做第一步位移Xid(k+1)2,如果此步位移得到搜索位置最好,则取之;否则进一步利用自身认知经验项得到位移点Xid(k+1)3,同进也可再利用社会认识经验得到 Xid(k+1).最后比较 Xid(k+1),Xid(k+1)2,Xid(k+1)3,取其最优者做为下一步的运动位置更新点. 综上所述,改进的PSO算法具有PSO算法的基本特点,简单,易实现,运算量较小等优点,同时兼顾了搜索效率和收敛精度,此外,新算法并未引入新的参数,这样就易于通用,因为新算法将搜索的中间值加以利用和分析,省去了参数调节的烦琐计算,因此新算法较简单通用. 在粒子群的进化过程中,当得到的最优解在连续的M次迭代中都无变化时,用一个计数器记录到目前为止停滞的代数T,可以这样设定:如果连续两次得到的最优解相同则将T增1,否则将其清0;当T≥M时,则说明算法可能停滞,在M次的迭代中,粒子没有能力跳出局部最优.此时,为加强粒子的对空间的搜索可以对某些粒子在概率性选择下进行随机重新初始化.搜索空间区域为:[XMind,XMaxd],在其内部重新初始化即为: 其中:β为事先设定的一个阈值,可取[0.8,1]. 在迭代过程中,当粒子有可能陷入局部极值时,为避免过大的破坏粒子原有的运行状态,仅选择少部分粒子进行重新初始化. 选用4个典型基准测试函数,与基本PSO及sPSO[18[18],HPSO-TVAC[15]等算法比较,验证CMPSO的可行性.这4个常用的基准函数、函数形式、搜索范围及维数、理论极值(极小值)和优化目标精度等见表1;其中:HPSO-TVAC,sPSO和tPSO参数设置与文献[18]与文献[15]一致,CMPSO参数设 置 为 :ω0=1.2,c1=c2=2,ω=ω0*exp(-0.5*k*k),μ=3.99,Max=10,β=0.8. 对算法性能评估采用如下方法[18]:(1)固定迭代次数下的实验效果对比;(2)固定收敛精度的实验效果对比. 固定代数下的的实验结果对比如图1所示,实验结果是采用独立运行50次后的平均值给出.其中:粒子数目为50,进化代数为1000;图1(a)~图1(h)是五种算法分别在测试函数f1~f8的适应度值的对数曲线(为方便显示统一加10-10做为适应度的截止值). 从图1-1(a)到图1-1(h)可以看出,PSO算法在1000代内都难以收敛到目标精度,其他改进算法表现在总体上均优于PSO算法.下面依次详细分析. 从图1-1中可以看出,CMPSO算法较其它四中算法均得到较大改进,对8个函数的优化来看基本上在100代以内都能收敛到目标精度,有的函数甚至在20代以内都能收敛到目标精度,可以说CMPSO算法表现是较其它算法是最佳的.其它算法中sPSO,再次是tPSO算法收敛情况较好.在对Rosenbrock函数f6(一个经典的复杂优化问题,取值区间内平坦,为算法提供了少量的信息,要收敛到全局最优位置的机会非常小,所以它一般用来测试算法的执行效率[19])及Schaffer’s函数f8这两个函数上,CMPSO将其改进后的开求精能力和开挖能力充分表现出来:如Rosenbrock函数f6,其在400代后又进一步向高精度深度求精;在Schaffer’s函数f8表现更为明显,在1000代以内不断向更高精度逼进,充分体现了其对空间的开挖能力和求精能力. 表1 8个基准测试函数 图1-1 f1~f8在5个实验中的适应度值进化曲线 表2 实验结果对比 因此,CMPSO算法改善了PSO算法对空间的全局搜索效果,提高了算法的收敛速度和精度,较为有效的避免了早熟问题,与其它改进算法相比也是有较大的改进,如:较tPSO算法参数少,更具有通用性;较sPSO收敛速度和精度也有较大的提高.因此,在固定迭代次数的前题下,CMPSO算法改进有效性得到有力证实. 作如下规定:同样是种群规模为50,在表1指定的收敛精度下,对达到收敛精度所需的迭代次数进行比较.由达到目标精度的最小值,均值,最大值,方差等方面加以考察.表2是由表1指定精度下独立50次所得 (如果算法在10000代内还没有收敛到目标精度于以终止). 由表2可见:在收敛速度上PSO算法最差,其次是HPSO-TVAC,这两个算法在大部分情况下不能收敛到目标精度,而其它三种算法基本上均能收敛到目标精度.CMPSO在固定收敛精度下,其收敛速度均优于其它算法,而sPSO在收敛速度上优于tPSO,三者中CMPSO表现最佳,说明了改进有效性. 本文在分析基本PSO算法收敛精度低,早熟等不足的基础上,受自然现象的启发,提出了一种改进型的PSO算法.用经典的测试函数来测试算法,经验证,充分表明了改进算法的有效性. 〔1〕Kennedy J,Eberhart R C.Particle swarm optimization [C].In:Proc.of the IEEE Internationa1 Conference on Neura1 Networks,Perth,Australia.1995,1942-1948. 〔2〕ShiY,EberhartR C.A modified particle swarm optimizer [C].In:Proc.of the IEEE International Conference on Evolutionary Computation.1998,69-73. 〔3〕Clerc M,Kennedy J.The particle swarm:Explosion stability and convergence in a multidimensional complex space[J].IEEE Trans.on Evolutionary Computation.2002,6(1):58-73. 〔4〕武忠勇,缑锦,赵志强.具有自适应邻域探测机制的改进型PSO算法[J].小型微型计算机系统,2010,31(9):1938-1945. 〔5〕郑宣耀,李欢,滕少华.自适应变邻域混沌搜索微粒群算法 [J].计算机工程与应用,2007,43(31):90-93. 〔6〕赵娜,张伏生,魏平,等.基于改进多粒子群算法的电力系统无功优化 [J].西安交通大学学报,2006,34(4):463-467. 〔7〕张勇,巩敦卫,张婉秋.一种基于单纯形法的改进微粒群优化算法及其收敛性分析[J].自动化学报,2009,35(3):289-298. 〔8〕Parsopoulos K E,Vrahatis M N.UPSO:A unified particle swarm optimization scheme[C].In:Proc.of the ICCM SE 2004.Attica.2004:868-873. 〔9〕Mendes R,Kennedy J,Neves J.The fully informed particle swarm:Simpler,maybe better[J].IEEE Trans.on Evolutionary Computation.2004,8(3):204-210. 〔10〕赫然,王永吉,王青,等.一种改进的自适应逃逸微粒群算法及实验分析 [J].软件学报,2005,16(12):2036-2044. 〔11〕Peram T,Veeramachaneni K.Fitness-Distance-Ratio based particle swarm optimization[C].In:Proc.of the IEEE Swarm Intelligence Symp.Indianapolis.2003,174-181. 〔12〕〔13〕Trelea IC.The particle swarm optimization algorithm:Convergence analysis and parameter selection [J].Information Processing Letters.2003,85(6):317-325. 〔14〕潘峰,陈杰,甘明刚,等.粒子群优化算法模型分析[J].自动化学报,2006,32(3):368-377. 〔15〕Ratanaweera A,Halgamuge S K,Watson H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients [J].IEEE Trans.on Evolutionary Computation,2004,8(3):240-255. 〔16〕Liang J J,Qin A K.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Trans.on Evolutionary Computation,2006,10(3):281-295. 〔17〕吕艳萍,李绍滋,陈水利,等.自适应扩散混合变异机制微粒群算法 [J].软件学报,2007,18(11):2740-2751. 〔18〕胡旺,李志蜀.一种简化而高效的粒子群优化算法[J].软件学报,2007,18(4):861-868. 〔19〕高芳,崔刚,吴智博,等.一种新型多步式位置可选择更新粒子群优化算法 [J].电子学报,2009,37(3):529-534. 〔20〕纪震,周家锐,廖惠连,等.智能单粒子优化算法[J].计算机学报,2010,33(2):556-561. TP18 A 1673-260X(2012)10-0015-052.4 重新初始化

3 实验及结果分析
3.1 实验设计
3.2 实验结果分析
3.2.1 固定迭代次数下的实验效果对比



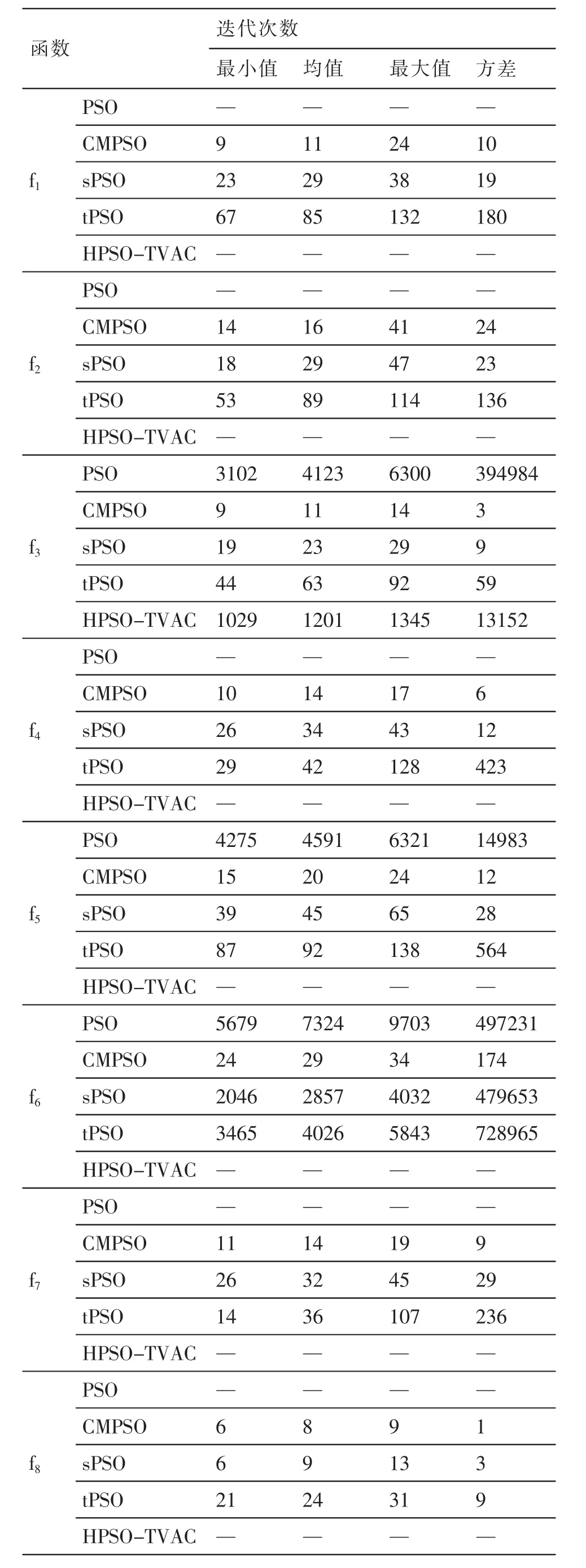
3.2.2 固定收敛精度的实验效果对比
4 总结

