基于BELLHOP模型的宽带信号波形预报

谢 骏, 笪良龙, 唐 帅, 范培勤

(海军潜艇学院, 山东 青岛266071)

水声传播通常主要采用窄带传播模型, 即从频域波动方程(赫姆霍兹方程)出发, 求解的是某一频率的声压场[1-2]。随着声纳孔径的增大, 工作频率越来越低, 水声领域也越来越多地采用宽带技术, 宽带波形预报是实现信号级声纳仿真系统的核心技术之一。

本文主要讨论基于 BELLHOP模型建立时域宽带模型的基本原理, 在此基础上, 重点分析 Pekeris环境下脉冲声传播波形预报问题, 并将波形预报仿真结果与BDRM频域宽带波形预报模型的仿真结果进行分析比对。

1 宽带传播模型

宽带技术主要采用频域傅立叶合成法或时域法,如图 1所示。傅立叶合成法是在频率范围内, 以 Δf为间隔(例如 Δf可以为 1Hz)的若干离散频率上多次执行现有的传播模型。然后通过适当的加权平均处理(即内插后置处理器), 将所得到的带宽内各个频率的传播损失加起来, 从而获得相当于整个频带的传播损失。原则上, 通过频域范围内对各个CW解进行傅立叶综合, 频域波动方程就能处理宽带信号。Jensen[3]总结了适合于海洋中低频声脉冲传播实际建模的波动理论技术, 强调了利用现有 CW 传播模型(基于简正波和抛物型方程近似)的傅立叶合成方法, 进行脉冲传播预报的计算效率问题。Jensen[4]进一步研究了这些问题, 将重点放在有泄漏的海面波导中的声传播。Futa和Kikuchi[5]研究了利用有限差分时域(FDTD)方法解决浅海中声脉冲传播问题。张仁和等[6-7]对脉冲信号波形预报进行了研究, 主要基于WKBZ和BDRM理论。由于海底底质参数对信号波形预报影响很大, 近年来主要开展了大量海底底质参数反演的实验研究[8-9]。McDonald和Kuperman[10]提出了对宽带线性脉冲在波导中的传播进行模拟的方法, 这是另一大类技术中的一个例子,称为时域方法[11]。在最新的研究中, Porter[12]提出了时间步进 FFP, 用于建模声脉冲信号在海洋中的传播。Collins[13]使用 TDPE模型研究基于脉冲传播的沉积层散射效应。Orchard等[14]提出三维TDPA(时域抛物近似)模型, 仿真三维海洋环境中的声脉冲传播。

2 基于射线的时域宽带模型

对于柱对称系统, 射线方程写为:

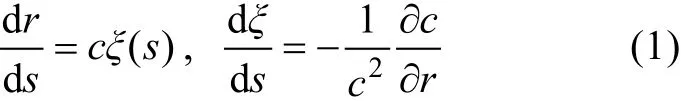
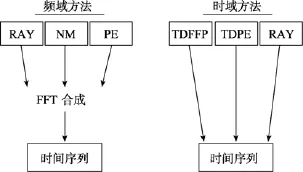
图1 宽带传播模型Fig. 1 Broadband propagation model

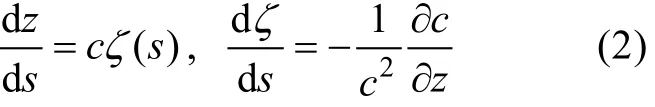
这里r(s)和z(s)是柱坐标系的射线坐标,s是沿射线的弧长,c(s)[ξ(s),ζ(s)]是沿射线的正切对。

z(s),r(s),ξ(s)和ζ(s)的初始条件是:

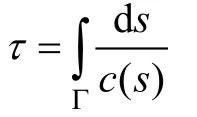
射线跟踪主要任务是通过求解射线方程求得射线坐标。幅度和声压可通过求解动力学方程得到, 这在文献[15]中有详细描述。

设单个本征声线所作贡献的单频表达式为:

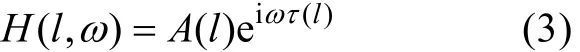
式中A(l)是由声线管横截面积决定的幅度,τ(l)是沿声线路径的相位延迟:

进一步假设损失与频率无关, 因而幅度项A(l)也与频率无关。对于中心频率为f0的窄谱声源, 我们可以根据对频率f0得到的损失来计算A(l)。另一方面, 如果损失与频率有简单关系, 只要微小的修改就可以继续进行下面的推导。

如前所述, 时域解可以通过傅立叶合成得到,即

式中S()ω是声源的谱。代入H(l,)ω的声线表达式得

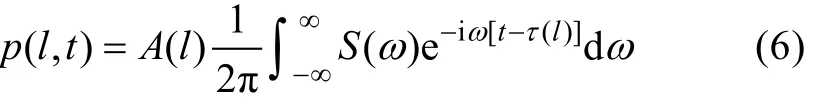
也就是

现在我们可以把谱积分看成是逆傅立叶变换, 故有

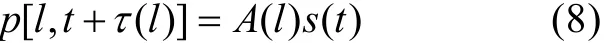
不失一般性, 上式可写成如下形式

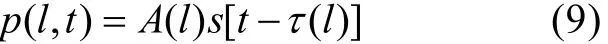
显然, 某号声线的接收信号就是声源信号波形按幅度按照A(l)加权, 并伴有τ(l)延迟的结果。因此有

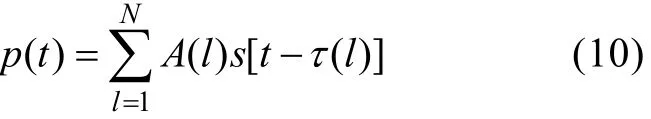
如果声源为δ脉冲, 上式变为

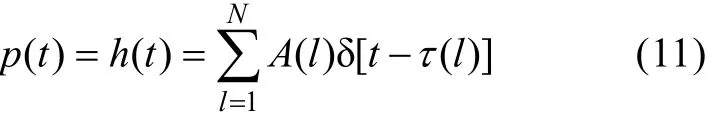
上式即为水声信道的系统响应函数,N为有效声线的个数。对其求傅立叶变换得到:

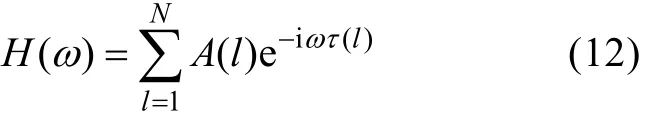
从射线声学的角度, 根据(11)式水声信道信号处理系统的结构可用图2表示:

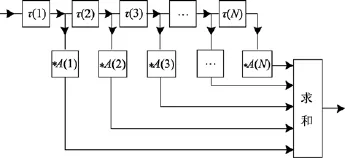
图2 基于射线的水声信道传输系统结构图Fig. 2 Underwater acoustic channel transmission system structure diagram based on ray model

根据数字信号处理知识可知, 图 2对脉冲信号进行延迟、加权和求和过程是典型的时域数字滤波器设计过程[16], 而且这种延迟求和会导致系统频域幅度响应函数呈现“梳状滤波器”形状, 实际上水声信道响应函数的确是呈现“梳状滤波器”结构的[17]。这主要由于本征声线掠射角是离散的, 在一个连续的时空中, 声传输过程被表征成了离散化的数字系统。

3 仿真结果分析

讨论两层液体介质的Pekeris环境模型脉冲声传播问题, Pekeris环境模型参数为: 海水深度100 m,海水声速1 500 m/s, 海水密度1.0 g/cm3, 海底声速1 680 m/s, 海底密度1.8 g/cm3, 吸收系数0.6 dB/λ,声源深度10 m, 接收深度10 m。

脉冲信号为

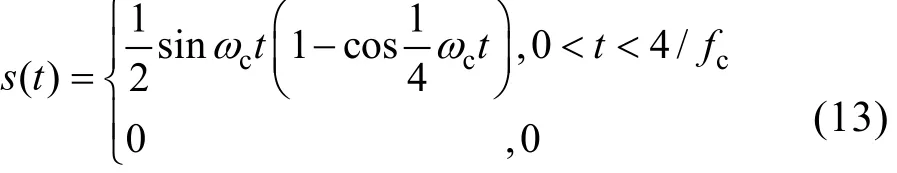
其中fc为中心频率。

基本射线模型采用Bellhop模型, 它是一种高效的射线跟踪程序,由Michael Porter采用Fortran 语言编写。Bellhop是二维声射线跟踪模型, 波导界面可以是水平不变的, 也可以是水平变化的。模型输出为射线坐标、传播时间、幅度、本征声线、声压或传播损失(相干、非相干和半相干)。声压计算基于高斯射线束理论[15,18], 可采用不同的近似, 主要有几何波束[19]; 射线中心坐标波束; 笛卡儿坐标波束; 高斯射线束近似[20]。

图3是在 Pekeris环境模型条件下 BDRM 与BELLHOP仿真中心频率 50 Hz, 带宽 50 Hz, 在30 km处接收脉冲波形, 两波形相关系数为80.3%。从图 3中可以看出, 两模型预报波形主要在第二个波包后沿差异较大, 前沿主要是高频的贡献, 后沿更多是低频的贡献, BELLHOP对较低频率声线的预报有较大误差。为进一步验证这一想法, 将信号中心频率调整到150 Hz, 带宽50 Hz, 图4中30 km处接收波形仿真结果, 接收波形相关系数高达 99%;22 km 处接收波形仿真结果, 接收波形相关系数为86.4%, 相关系数变小的原因是两模型计算时延误差引起的。

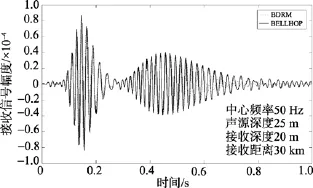
图3 BDRM与BELLHOP仿真接收波形对比Fig. 3 Receiving waveform comparison based on BDRM and BELLHOP model

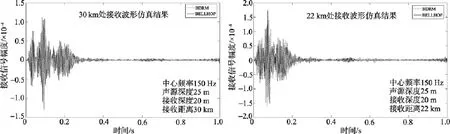
图4 不同接收距离接收波形仿真结果Fig. 4 Receiving waveform simulation results of different receiving distances

在一定条件下, 射线模型与简正波模型具有同等计算精度, 由于射线模型通过一次计算就能得到所有本征声线的幅度和延迟, 相对于简正波模型来说, 能够很方便快速的构造出信道传输函数。同时利用射线模型, 能够方便的选择仅接收特定角度出射的本征声线, 图5是中心频率50 Hz, 带宽50 Hz脉冲在30 km处对不同角度出射声线的接收波形仿真结果。

4 结论

以信号级声纳仿真系统的需求为牵引, 在对射线模型的基本原理分析的基础上, 推导了基于射线的时域宽带传播模型, 从射线声学角度理解水声信道, 其本质是对脉冲信号进行延迟、加权和求和, 是典型的时域数字式“梳状滤波器”。仿真结果分析表明, 在一定条件下, 射线模型与简正波模型具有同等计算精度, 由于射线模型通过一次计算就能得到所有本征声线的幅度和延迟, 相对于简正波模型来说, 能够更快速地构造出信道传输函数, 同时能够更直观地控制声纳垂直接收角的仿真。

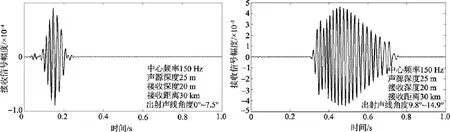
图5 不同角度出射声线的接收波形仿真结果图Fig. 5 Receiving waveform simulation results of different angles outgoing sound ray

[1]杨士莪. 水声传播原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 1990.

[2]布列霍夫斯基. 分层介质中的波(中译本)[M]. 北京:科学出版社, 1985.

[3]Jensen F B. Wave theory modeling: a convenient approach to CW and pulse propagation modeling in low-frequency acoustics[J]. IEEE J Oceanic Eng, 1988,13(1): 186-197.

[4]Jensen F B. CW and pulse propagation modeling in ocean acoustics[C]//Moura J M F, Lourtie I M G.Acoustic Signal Processing for Ocean Exploration.Dordrecht, the Netherlands: Kluwer Academic Publishers, 1993: 3-20.

[5]Futa K, Kikuchi T. Finite difference time domain analysis of bottom effect on sound propagation in shallow water[J].Acoust Sci Technol, 2001, 22: 303-305.

[6]何怡, 张仁和, 朱业. 水下声道中脉冲传播的 WKBZ简正波方法[J]. 声学学报, 1994, 19(6): 418-424.

[7]朱业, 张仁和. 负跃层浅海中的脉冲声传播[J]. 中国科学(A辑), 1996, 26(3): 271-279.

[8]张学磊, 李整林, 张仁和.利用船辐射噪声反演海底吸收[J]. 声学技术, 2007, 26(5): 994-995.

[9]李整林, 鄢锦, 李风华, 等.由简正波群延时及幅度反演海底参数[J]. 声学学报, 2002, 27(6): 487-491.

[10]McDonald B E, Kuperman W A. Time domain formulation for pulse propagation including nonlinear behavior at a caustic[J]. J Acoustic Soc Amer, 1987, 81(5):1406-1417.

[11]Kuperman W. A models of sound propagation in the Ocean[J]. Nav Res Rev, 1985, 37(3): 32-41.

[12]Porter M B. The time-marched fast-field program (FFP)for modeling acoustic pulse propagation[J]. J Acoustic Soc Amer, 1990, 87(5): 2013-2023.

[13]Collins M D. The time-domain solution of the wide-angle parabolic equation including the effects of sediment dispersion[J]. J Acoustic Soc Amer, 1988,84(6): 2114-2125.

[14]Orchard B J, Siegmann W L, Jacobson M J.Three-dimensional time-domain paraxial approximations for ocean acoustic wave propagation[J]. J Acoustic Soc Amer, 1992, 91(2): 788-801.

[15]Porter M B, Bucker H P. Gaussian beam tracing for computing ocean acoustic fields[J]. J Acoust Soc America, 1987, 82(4): 1349-1359.

[16]Karrenberg U. 信号处理的交互式多媒体教程[M].李秀梅, 肖泳, 毕国安, 译. 北京: 清华大学出版社,2008: 263-267 .

[17]惠俊英, 生雪莉. 水下声信道[M]. 北京: 国防工业出版社, 2007: 37-39.

[18]Jensen F, Kuperman W, Porter M, et al. Computational Ocean Acoustics[M]. New York: Springer, 1994:126-128.

[19]Porter M B, Liu Yong-chun. Finite-element ray tracing[C]//Lee D, Schultz M H. Proceedings of the International Conference on Theoretical and Computational Acoustics. Singapore: World Scientific, 1994: 947-956.

[20]Weinberg H, Keenan R E. Gaussian ray bundless for modeling high-frequency propagation loss under shallow-water conditions[J]. J Acoustic Soc America, 1996,100(3): 1421-1431.