基于小波变换的大跨度桥梁上车轮轴间距和车速监测

周志红，吴邵庆，费庆国

(1.东南大学土木工程学院，江苏南京 210096;2.江苏省工程力学分析重点实验室，江苏南京 210096)

随着我国公路交通事业的发展，超重超速车辆逐渐成为人们关注的主要问题，直接影响桥梁的工作状态和使用寿命［1］。同时，随着许多大跨度、轻质化、大柔度新型桥梁的大量涌现，车载特性直接影响桥梁动力响应特性，这使得移动车辆荷载作用下桥梁的动力响应问题成为有关研究者关注的热点［2］。

在车桥耦合振动问题中，车辆模型可分为整车模型、半车模型和单轮车辆模型等［3-4］。求解车桥系统动力学方程的方法又分为直接积分法和振型叠加法。赵永刚等［5］考虑桥梁路边不平整度，建立了大跨度斜拉桥空间有限元模型，并利用随机分析方法获得桥梁动响应。肖新标等［6］建立了匀速移动质量模型作用下的简支梁动态响应模型，实现了车桥耦合振动系统的仿真，其仿真结果具有快速、简单和灵活的特点。Moghimi等［7］利用仿真分析了车速等因素对车桥耦合系统的影响。王解军等［8］建立了适用于大跨桥梁车辆振动计算的车桥耦合单元模型，分析比较了重型汽车与轻型汽车作用下的动力冲击系数。然而以上方法均侧重于理论分析，未应用于实际工程。刘文淑等［9］利用小波的多尺度分析，对实测钢箱梁上的应力数据去噪，使得处理后的数据更能反映真实应力水平，但未应用实测响应数据进行车桥系统参数的识别。

本文将小波变换技术引入车轴轮间距和车速监测中，提出一种针对大跨度桥梁上车轮轴间距和车速监测的新型数据处理方法。根据车轮过桥时桥面的动响应，实现对大跨度桥梁结构上车辆行驶状况的监测，所提方法能够较准确地得到车轮轴间距、车速和车辆进入/离开桥梁的时间间隔。

1 基于小波变换的车轮轴间距和车速状态监测原理

小波变换作为一种时频分析工具，与传统傅里叶变换相比，能够很好地捕捉不同频率下信号分量的局部信息，并准确解构和重建有限的非周期和非平稳信号［10-12］，在信号分析和参数识别中具有明显的优势，并有较多的工程应用。小波变换包括连续小波变换(CWT)和离散小波变换(DWT)等，本文利用基于DWT的方法对桥上车辆状态进行检测识别分析。具体思路为:利用小波的多尺度分析将车辆经过时实测桥面动应变数据进行多尺度分解，利用每个尺度上的小波系数的峰值来检测车轮入桥和出桥的时刻，通过车辆过桥的时间以及前后轮在桥上停留时间来计算车的实际速度，然后根据前后轮入桥和出桥引起的动应力峰值来识别车轮轴间距。

2 青衣南大桥实例验证

为验证本文方法在大跨度桥梁结构车辆车轮轴间距和车速监测中的适用性，将该方法应用于香港青衣南大桥监测中。香港青衣南大桥为三跨连续混凝土桥梁，总长73 m，宽10.58 m，水平方向倾斜角为27°，即该桥的纵向斜率为6.75%。采用双箱梁型截面，钢筋混凝土结构的等效弹性模量为26 GPa，密度为24.5 kN/m2。具体步骤为:(a)对香港青衣南大桥建立有限元模型，利用动力学分析得到行车状态下桥面各处的动态应变信号，利用基于DWT的方法进行车速、车轮轴间距的识别;(b)根据桥上实测数据，同样利用基于DWT的方法进行车速、车轮轴间距的识别，验证本文提出的方法的适用性。

2.1 有限元数值仿真

图1为建立的有限元模型以及测点排布示意图。假设车轮轴间距为4.3 m，车速为20 m/s情况下，利用基于有限元模型动力学分析结果得到各处的动应变结果，动应变信号的采样频率为100 Hz。

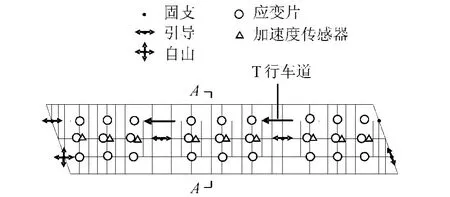
图1 有限元模型中应变片排布位置Fig.1 Strain gauge installation on finite element model

基于DWT的方法，采用‘db4’小波对单一车辆入桥时桥上动应变信号进行10个尺度的分解，图2为某动应变信号在尺度1的细节信号。从图2可以发现，信号中出现了与两车轮轴入桥相对应的2个峰值，峰值之间包含22个时间步长，即后轴入桥比前轴早0.22 s。如假设车速为20 m/s且事先已知，则可以计算得到车轮轴间距为4.4 m，与实际车轮轴间距4.3 m非常接近。识别桥上车辆的车速可以根据已知距离的2个应变片的信号或其DWT分解结果计算得到。车载作用下的桥梁，由于车轮作用点越靠近应变片，对应的动应变信号幅值就越大，因此，可以将两应变片的距离除以两应变信号达到峰值的时间差来获得车轮的行驶速度。

2.1.1 噪声水平对识别结果的影响

由于试验数据往往包含噪声，在此考虑信噪比(SNR)分别为10dB和20dB的车轮轴间距识别效果。依然采用基于DWT的方法将带噪声的信号进行10个尺度的分解，取出第4个尺度的细节来识别车轮轴间距，识别结果见表1。由表1可知，包含噪声的原始信号的识别精度低于无噪声情况，随着动应变信号信噪比的降低，车轮轴间距的识别误差会增加。

图2 某动应变信号在尺度1的细节信号Fig.2 Detail strain signal at level 1

2.1.2 小波类型和车速对识别结果的影响

采用不同小波类型以及车速对识别结果的影响见表2。由表2可以看出，不同的小波类型对识别结果有一定的影响，除基于‘db4’小波的识别精度随着车速的增大而降低以外，其他类型的小波识别精度都随着车速的增大而减小。其原因可以归结于各小波的特点:‘db4’小波从本质上属于离散小波，能够用小波系数精确地描述信号细节;而其他小波如‘haar’或‘sym4’，其本身就有明确的表达式。当车速较快，动应变信号包含较多高频分量时，细节分量的峰值将会出现偏移，导致识别精度下降。总体来说，随着车速的降低，车轮轴间距的识别精度有所提高，因此在车速较高时，建议采用‘db4’小波。

表1 考虑噪声时的车轮轴间距识别Table 1 Vehicle axle spacing identification with consideration of noise

表2 不同小波类型以及车速下车轮轴间距的识别结果Table 2 Vehicle axle spacing identification with different wavelets and vehicle speeds

2.2 基于实测数据监测和识别验证

为了应用本文提出的方法进行车轮轴间距的识别和车速的检测，在香港青衣南大桥上进行振动测试。在三跨桥的边跨布置传感器，标准卡车经过桥面时，获得如图3所示传感器布置方案下的2，5，8，11和14位置的动应变数据。现场测试采样频率为500 Hz，所用的标准车辆为三轴车辆，其中第1和第2轮轴间距为4.43 m，第2和第3轮轴间距为1.32 m。利用布置的两已知距离的光栅传感器测得经过时刻，将传感器距离除以经过的总时间计算得到(在试验中尽量保持车辆匀速行驶)车速为15.28 m/s。

2.2.1 车轮轴间距和车速监测

由于实测数据中桥面动应变数据的信噪比较低，利用基于DWT的方法得到各细节部分信号由于车轮经过应变片产生的峰值较难判断，因此还需引入信号的近似部分来识别车轮轴间距和车速。信号的近似部分受噪声影响较小。图4为布置在第1跨跨中两边的典型应变片采集到的信号的近似部分，由图4可知，近似信号中的突变由车轮轴入桥引起，可以根据3个突变位置的时刻来计算轴间距。由此识别得到的车轮轴间距和车速见表3(采用第4尺度的近似信号)。

图3 现场测试中应变片排布位置Fig.3 Strain gauge installation in field test

由于试验测得的信号信噪比较低，利用信号细节部分识别会难以判断峰值，通过近似信号可以较好地识别间距相对较大的第1和第2轮轴间距，而对间距很小(两轮胎紧挨)的车轮轴间距识别误差较大。相比之下，车速监测的准确度相对较高。识别精度也与实测信号的质量有关，不同传感器其信号识别效果不同，建议选择质量较高的传感器分别识别之后进行平均，以获得更好的识别结果。

图4 第一跨跨中位置前/后应变片信号近似部分Fig.4 Approximations for two strain signals before/after mid-span of first span

3 结 语

本文利用小波变换，提出一种基于桥面实测动应变数据来获得桥梁车辆信息的识别方法，以实现对大跨度桥梁结构上车辆行驶状况的监测。数值仿真结果表明:采用基于DWT的方法能够较为准确地得到桥上车轮轴间距和车速的信息，车速大小、噪声水平以及所采用的小波种类都会对识别结果产生影响。香港青衣南大桥现场测试分析表明，基于DWT的方法在实际大跨混凝土桥梁上行车监测是可行的，识别得到的车速精度略高于车轮轴间距的精度，同时，车轮轴间距的大小对识别精度的影响也较大，从动应变信号中能够较为准确地识别前后轮距较大的车轮轴间距，对于标准车第2轴和第3轴车轮紧挨、轴间距很短的情况，识别精度较低，证明了采用基于DWT方法的有效性。

表3 由近似部分信号识别得到的车轮轴间距和车速Table 3 Vehicle axle spacing and speed identification from approximation signals

［1］朱劲松，肖汝诚，何立志.大跨度斜拉桥智能可靠度评估方法研究［J］.土木工程学报，2007，40(5):41-48.(ZHU Jinsong，XIAO Rucheng，HE Lizhi.Reliability assessment of large-span cable-stayed bridges based on artificial intelligence［J］.China Civil Engineering Journal，2007，40(5):41-48.(in Chinese))

［2］MICHALTSOS G T.Dynamic behaviour of a single-span beam subjected to loads moving with variable speeds［J］.Journal of Sound and Vibration，2002，258(2):359-372.

［3］李小珍，张黎明，张洁.公路桥梁与车辆耦合振动研究现状与发展趋势［J］.工程力学，2008，25(3):230-240.(LI Xiaozhen，ZHANG Liming，ZHANGJie.State-of-the-art review and trend of studies on coupling vibration for vehicle and highway bridge system［J］.Engineering Mechanics，2008，25(3):230-240.(in Chinese))

［4］张洁.公路车辆与桥梁耦合振动分析研究［D］.成都:西南交通大学，2007.

［5］赵永刚，盛洪飞，陈明非.大跨度斜拉桥车-桥耦合振动分析的数值解法［J］.公路工程，2009，34(1):143-146.(ZHAO Yonggang，SHENG Hongfei，CHEN Mingfei.Numerical method based on vehicle-bridge coupling vibration analysis of large span cable-stayed bridges［J］.Highway Engineering，2009，34(1):143-146.(in Chinese))

［6］肖新标，沈火明.移动荷载作用下桥梁的系统仿真［J］.振动与冲击，2005，24(1):121-123.(XIAO Xinbiao，SHEN Huoming.Dynamic simulation of bridge subjected to moving load［J］.Journal of Vibration and Shock，2005，24(1):121-123.(in Chinese))

［7］MOGHIMI H，RONAGH H R.Impact factors for a composite steel bridge non-linear dynamic simulation［J］.International Journal of Impact Engineering，2008，35:1228-1243.

［8］王解军，张伟，吴卫祥.重型汽车荷载作用下简支梁桥的动力反应分析［J］.中南公路工程，2005，30(2):55-62.(WANGJiejun，ZHANG Wei，WU Weixiang.Analysis of dynamic responses of simply supported girder bridge under heavy moving vehicles［J］.Central South Highway Engineering，2005，30(2):55-62.(in Chinese))

［9］刘文淑，林咸志，薛涛，等.基于小波变换的钢箱梁应力监测多尺度分析［J］.河海大学学报:自然科学版，2010，38(4):407-410.(LIU Wenshu，LIN Xianzhi，XUE Tao，et al.Multi-scale analysis of stress monitoring of steel box girders based on wavelet transform［J］.Journal of Hohai University:Nature Science，2010，38(4):407-410.(in Chinese))

［10］LIU Zejia，JIANG Bin，TANG Liqun.Features of long-term health monitored strains of a bridge with wavelet analysis［J］.Theoretical and Applied Mechanics Letters，2011，1(5):051006-051009.

［11］CAPRIOI L，CIGADA A，RAVEGLIA D.Rail inspection in track maintenance:a benchmark between the wavelet approach and the more conventional fourier analysis［J］.Mechanical Systems and Signal Processing，2007，21:631-652.

［12］魏明果.实用小波分析［M］.北京:北京理工大学出版社，2005.