稳定渗流分析的局部间断伽辽金有限元法
何朝葵 ,速宝玉 ,盛金昌
(1.河海大学水利水电学院,江苏 南京 210098;2.河海大学理学院,江苏 南京 210098)
间断有限元法[1-3]是一种在有限元法、有限体积法和有限差分法基础上发展起来的数值计算方法,它的特点在于允许插值函数在剖分单元边界处不连续,使得其在处理大梯度问题上具有独特的优势,并使其在多个领域得到广泛的应用[2-4].国外部分学者对间断有限元法在椭圆问题上的应用进行了分析[5-6],国内则鲜见这方面的文献.局部间断伽辽金有限元法[2,7](the local discontinuous Galerkin methods,简称LDG法)是间断有限元法中最有效的方法之一,它具有良好的稳定性.笔者主要从理论上分析LDG法在稳定渗流分析问题中的应用.
1 渗流方程
稳定渗流方程及定解条件如下:

式中:Ω——求解区域;H——水头函数;k——渗透系数(考虑各向同性,分片常数情形);ΓD,ΓN——第一类边界和第二类边界,且∂Ω=ΓD∪ΓN;n——边界ΓN上的外法线方向单位向量;gD,gN——常数.
2 LDG法原理
把水力梯度 σ=k▽H作为中间变量,则式(1)中的二阶方程化为一阶方程组:

假设 Th为Ω的1个剖分,E表示其中的任意1个单元,nE表示E的单位外法线方向向量.用 σh和Hh表示单元内插值函数,LDG法允许插值函数在单元边界处不连续,故插值函数在单元边界上的值用数值流通量[1-3]替代.数值流通量定义如下:

若e为单元E和单元E′的公共边界,用 nE表示单元E在边界e上的外法线单位向量,Hh,E和 σh,E分别表示 Hh和 σh在边界上单元E侧的值,则有

式中:α——边界e上的常数;β——边界e上的常向量.
在式(2)中第1个方程两边分别乘以测试函数v,在第2个方程两边分别乘以测试向量函数τ,然后在每个单元上积分,得

式中:▽h——单元内梯度算子;kE——单元E的渗透系数.
单元方程(式(3)和式(4))通过数值流通量建立联系,构成整体代数方程.
3 基本计算格式
相对于剖分 Th,ε表示剖分单元边界的集合,ε0表示区域内部的单元边界的集合,εD表示在ΓD上的单元边界的集合,εN表示在ΓN上的单元边界的集合,要求 ε=ε0+εD+εN.把式(3)和式(4)相对于剖分 Th在求解域Ω上对所有单元叠加,整理得
式(5)和式(6)就称为渗流问题的LDG法基本计算格式.
4 变分形式的稳定性和有界性
由式(6)可得 σh在有限元空间 ∑h上的L2投影:

式中 ∏为投影算子.把式(7)代入式(5),整理得基本计算格式的变分形式为

其中

显然Bh(Hh,v)是对称双线性算子.为证明变分的稳定性和有界性,定义如下半范数和范数[8-10]:

引理
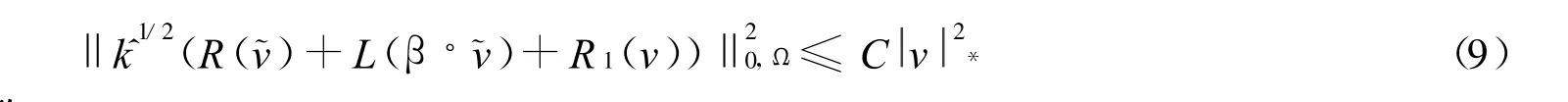
其中C是与h无关的常数.
证明

再由L2投影的稳定性可得不等式(9).
利用引理可以得 Bh(Hh,v)的稳定性,即对∀v∈Vh有

同样利用引理亦可得到Bh(v,v)的有界性,即对 ∀v,w∈Vh有


结合引理有
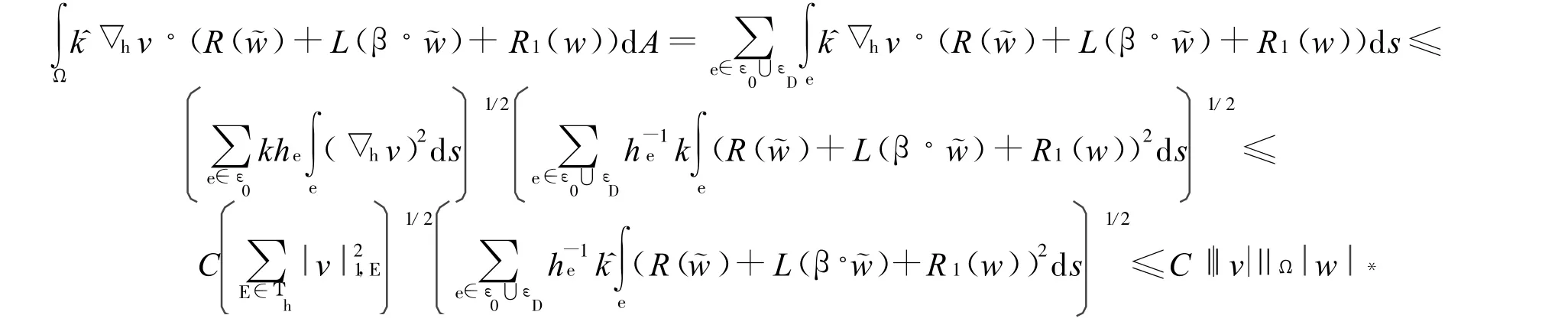
因而

根据Lax-Milgram定理知变分问题Bh(Hh,v)=Fh(v)存在唯一解.
5 误差估计
设H为渗流问题(式(1))的解,HI为相对剖分 Th下的某一插值函数,则由插值函数局部估计有

其中的常数C仅与插值函数的次数p和单元E的最小角度有关.为了得到LDG法数值解误差的L2估计,先看2个定理[11]:
定理1 若H为式(1)的解,H I为H的某个插值函数,则存在正数C使得式(13)成立.

证明

由迹不等式知存在常数C,使得

定理2 若H为式(1)的解,Hh为式(8)的解,则存在正数C使得式(15)成立.

证明 设 H I为 H的分片插值函数,由式(11)和式(12)有

由定理1和定理2可得到误差的L2估计.
定理3 若 H为式(1)的解,Hh为式(8)的解,则存在正数C使得式(16)成立.

证明 由于LDG法的数值流通量是守恒的,因而变分格式(8)是自相容的,即对 ∀v∈H2(Th)有Bh(v,,其中 ψ为方程-Δψ=g,(x,y)∈ Ω以及 ψ=0,(x,y)∈ ∂Ω的解[10].若取g=H-Hh,则有Bh(v,ψ)=(H-Hh,v),∀v ∈ Vh.设 ψI为 ψ的线性插值 ,则

6 结 语
间断有限元法已推广到水动力、气动力学等多个领域.笔者通过对稳定渗流分析的局部间断伽辽金有限元法的理论分析,给出其计算格式,并论证说明该格式具有良好的稳定性.论证结果表明,运用局部间断伽辽金有限元法来处理稳定渗流分析是有效的;在运用本文格式计算时,可以通过选取正交的基函数来简化整体代数方程组.对这一方法的近似解进行的先验误差分析表明其具有p+1阶精度,所以相对于一般的有限元法来说,局部间断伽辽金有限元法是一种具有较高精度的数值计算方法.关于局部间断伽辽金有限元法在渗流问题上的一些具体计算及验证可见文献[12],其他一些结论笔者正在整理中.
[1]REED WH,HILL T R.Triangular mesh methods for the neutron transport equation[R].Alamos:Los Alamos Scientific Laboratory,1973.
[2]COCKBURN B,KAMIADAKISG,SHU Chi-wang,et al.Discontinuous Galerkin Methods[M].Berlin:Spring Verlag,2000:89-101.
[3]刘儒勋,舒其望.计算流体力学的若干新方法[M].北京:科学出版社,2003:159-179.
[4]FAGHERAZZIS,FURBISH D J,RASETARINERA P,et al.Application of the discontinuous spectral Galerkinmethod togroundwater flow[J].Advances in Water Resources,2004,27:129-140.
[5]ARNOLD DN,BREZZIF,COCKBURN B,et al.Unified analysis of discontinuous Galerkinmethodsfor elliptic problems[J].SIAM J Numer Anal,2002,39(5):1749-1779.
[6]CASTILLO P.Performance of discontinuous Galerkin methods for elliptic pde's[J].SIAM JSci Comput,2002 ,24(2):524-547.
[7]COCKBURN B,SHU Chi-wang.The local discontinuous Galerkin finite element method for convection-diffusion systems[J].SIAM J Numer Anal,1998,35:2440-2463.
[8]CASTILLO P,PERUGIA I,SCHOTZAU D.An a priori error analysis of the local discontinuous Galerkin method for elliptic problems[J].SIAM JNumer Anal,2000,38:1676-1706.
[9]PERUGIA I,SCHOTZAU D.An hp-analysis of the local discontinuous Galerkin method for diffusion problems[J].JSci Comp,2002,17:561-571.
[10]肖捷,刘韶鹏.求解间断系数椭圆型问题的一种改进的DG方法[J].计算数学,2007,29(4):377-390.(XIAO Jie,LIU Shao-peng.A modified DG method for elliptic problems with discontinuous coefficients[J].Journal of Cumputational Mathematics,2007,29(4):377-390.(in Chinese)).
[11]LEEMA ,SHINJY.Error estimiates for a discontinuous Galerkinmethod for elliptic problems[J].Appl Math&Computing,2006,21(1/2):189-201.
[12]何朝葵,速宝玉,盛金昌,等.用局部间断伽辽金有限元法分析渗流场[J].水利水电科技进展,2010,30(2):21-23.(HE Zhao-kui,SU Bao-yu,SHENG Jin-chang,et al.Analysis of seepage field for aquifer problems by the local discontinuous Galerkin method[J].Advances in Science and Technology of Water Resources,2010,30(2):21-23.(in Chinese)).

