土水特征曲线的一个滞回模型
陆业奇,刘斯宏,傅中志
(河海大学水工结构研究所,江苏南京 210098)
非饱和土是多相混合体,通常认为是由土骨架、孔隙水和孔隙气三相组成.Fredlund等[1]认为:应将收缩膜(液-气分界面)作为独立的第四相,其状态对非饱和土的强度、变形等特性均具有显著的影响;建立非饱和土平衡条件时,需要同时考虑土体的整体平衡和收缩膜的局部平衡,故建议采用净应力和基质吸力2个应力变量来描述非饱和土的应力状态.Fredlund的双应力变量物理意义明确,且在试验中可以独立控制,在20世纪90年代非饱和土本构模型研究中得到了广泛的运用[2-3].但基于净应力和基质吸力的本构模型在数值计算中有诸多不便:非饱和土数值计算中通常假定孔隙气压力为常量,故净应力与基质吸力分别对应总应力与负孔压,无法实现非饱和状态与饱和状态之间的连续过渡[4].正因为如此,许多学者近年来重新审视了Bishop的广义有效应力原理[5-6],并提出了一系列基于广义有效应力与基质吸力的本构模型[7-8].
运用Bishop建议的有效应力必然涉及有效应力组合系数 χ的选择.原则上 χ可以作为饱和度Sw的函数,亦可取作基质吸力s的函数[9].Houlsby[10]通过能量分析指出:若将Bishop有效应力公式(1)中的 χ取为Sw,则有效应力与应变共轭,s与体积含水率nSw共轭,这为采用广义有效应力原理提供了理论基础.

采用Sw作为 χ还可以直接反应出土体含水量对材料强度、变形等力学特性的影响[9].此外,对土体的总应力平衡方程和孔隙水的连续性方程进行有限元离散后可以发现,当 χ=Sw时,单元的劲度矩阵是对称的,这对于提高非饱和土问题的求解效率极具意义.鉴于上述原因,非饱和土计算中广泛采用饱和度作为有效应力组合系数[11].
从数值计算的角度来说,采用饱和度作为有效应力组合系数必须建立饱和度与基质吸力之间的关系,同时进行力学和水力学分析(通常是耦合的),从而逐步完成初边值问题的求解.可见,除材料的力学本构模型外,还必须建立描述饱和度与基质吸力关系的水力学本构模型.土力学研究历史中,对力学本构模型进行了大量的研究,建立了弹塑性、亚塑性、边界面塑性等丰富的建模体系,并针对土体的不同变形特性提出了大量的本构模型.相比而言,水力学本构模型得到的重视程度远低于力学本构模型,在处理具体问题时通常仅采用脱湿曲线或者吸湿曲线,而忽略滞回特性,在涉及干湿循环过程时,得到的解答一般不能反应土体的实际含水量变化.
近年来,部分学者吸收了力学本构模型建模过程中的基本概念和方法,建立了全面考虑吸湿曲线、脱湿曲线和扫描曲线的数学模型.Wei等[12]基于热力学2个基本定律,认为毛细松弛和毛细滞回都是一种耗散过程,可以借助内变量来表征这一过程,并提出一个用内变量来考虑毛细滞回的模型.Li[13]基于边界面塑性理论,定义了给定饱和度时扫描曲线与边界曲线(主吸湿曲线和主脱湿曲线)斜率之间的关系,并通过积分建立了扫描曲线的表达式.刘艳等[14]对Wei和Li等的工作进行了分析,将不可恢复的含水率作为内变量,提出了一个修正的简化模型,并运用试验对该模型进行了检验.
本文以Li模型为例,研究了边界面水力学本构模型的特点,并指出Li模型预测的扫描曲线易于出界的不足,提出了克服该不足的方法,并建立了一个新的水力学模型.由于以饱和度作为状态变量的数值计算中需根据基质吸力确定饱和度,故本文模型将体积含水量作为因变量,以基质吸力作为自变量.
1 Li滞回模型简介
Li将土体的主吸湿曲线(fd(,Sr)=0)和主脱湿曲线(fw(,Sr)=0)作为2条边界曲线,限定所有的扫描曲线(f(s,Sr)=0)必须位于两者之间,且当扫描曲线接近边界曲线时,两者斜率逐渐趋同,以保证扫描曲线与边界曲线融合.为建立扫描曲线斜率与边界曲线斜率之间的关系,Li将干湿转换点 α作为记忆量,并在趋近的边界曲线上定义 α的映射点,如图1所示.为数学运算方便,Li对基质吸力s取对数(s*=ln s),并在半对数图s*~Sr中分析扫描曲线与边界曲线斜率之间的关系,如图2所示.

图1 水力状态变量定义Fig.1 Definitions of hydraulic state variables

图2 吸湿/脱湿路径和水力状态变量的变化Fig.2 Update of wetting/drying paths and hydraulic state variables
现记扫描曲线上的饱和度增量为d Sr,相应的基质吸力增量为d s*,并记增量d s*在趋近的边界曲线上的映射增量为d*.Li基于对试验结果的观察,认为始终大于等于1,且该比值取决于 s*同 α*和*之间的距离.当 s*趋近于 α*时可近似为无穷大;当s*趋近于*时,该比值趋近于1.由此Li给出了式(2),以表征 d s*,d*的关系:

式中β是该模型唯一参数,可以通过试验数据进行标定.
现将式(2)从干湿转化点α*到当前吸力状态s*进行如下积分:

可以得到封闭形式的扫描曲线表达式:

式中“+”用于脱湿过程,“-”用于吸湿过程.对于每一个给定的饱和度Sr,式(4)右端均为已知,由此即可计算相应的对数吸力值s*,并给出任意干湿过程中的扫描曲线.
笔者对一些试验进行模拟时发现,Li模型能够较好地重现扫描曲线,但亦存在不合理之处,即预测的扫描曲线可穿越边界,如图3所示.脱湿扫描曲线在A点之后与主脱湿曲线(MDC)的斜率近似相同,但扫描曲线穿越了主吸湿曲线(MWC),这与引入边界面的初衷相悖.实际上,式(2)仅保证了脱湿过程中扫描曲线不穿越MDC,仅通过斜率条件无法完全控制扫描曲线的形态.在实际运用中,一旦预测的扫描曲线出界,其后续的干湿循环过程不可能再得到合理的模拟.Li还指出,该模型只能直接得到给定饱和度增量情况下吸力的变化;在非饱和土有限元计算中,通常需根据吸力变化求解饱和度增量,这可以通过迭代计算[13]确定,但这对于提高数值计算的效率是不利的.

图3 预测扫描线出界Fig.3 Predicted scanning curve out of boundary
2 一个新的滞回模型
2.1 基本模型的建立
笔者参照Li的建模思路,通过扫描曲线体积含水率增量与边界曲线体积含水率增量之间的关系,来建立扫描曲线表达式.假定土体在(θ0,s)点发生干湿转换,该记忆量在趋近边界曲线上的投影记为(,s),如图4所示.现设土体状态由(θ,s)变化为(θ+dθ,s+d s),相应的投影点由(,s)变化为(+d,s+d s),则给定吸力增量d s时,必然有dθ≤d,为满足该条件,可设

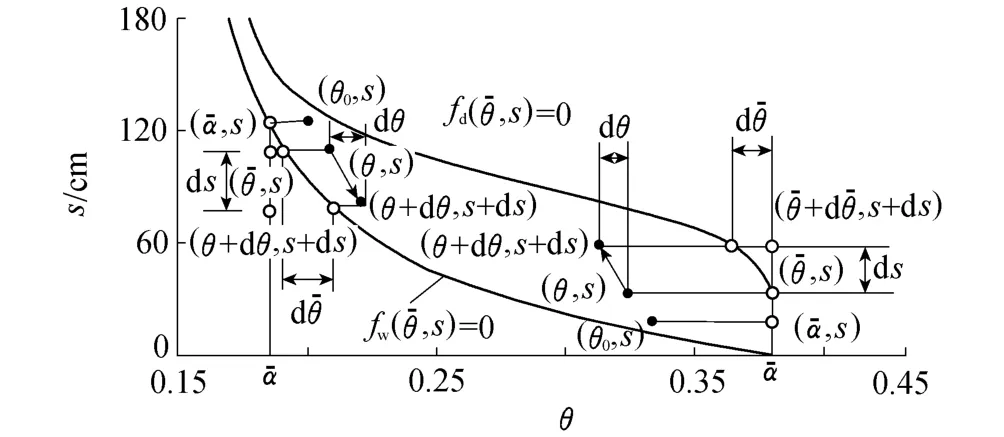
图4 模型状态变量定义(吸力以水头表示)Fig.4 Definitions of state variables(suction marked with water head)
对式(5)两端积分可得

式中θ0为干湿转换记忆点的体积含水率.式(6)可以显式地表达如下:

式中“-”用于脱湿过程,“+”用于吸湿过程.
这样就建立了吸力变化驱动体积含水率变化的滞回模型,该模型与Li模型相似,仅含有一个参数β.值得指出的是式(7)建立的模型并未解决扫描曲线出界的问题,下面对Li的基本模型进行修正.
2.2 出界问题的处理
如前所述,仅通过扫描曲线与边界曲线的斜率关系不足以对扫描曲线的范围进行全面的控制,建模过程中宜同时使用2条边界曲线共同确定扫描曲线.现将扫描曲线的体积含水率θ分成θ1和θ2:其中θ1为脱湿和吸湿过程中相应的边界曲线对扫描曲线的贡献,可由(7)式得到;θ2为另一条边界曲线对扫描曲线的贡献.在脱湿过程中可令
类似地,在吸湿过程中令

式中:θWT(s),θDR(s)——给定吸力下,主吸湿曲线和主脱湿曲线上的体积含水率.本文采用Feng等[15]建议的函数,即

式中:b,d——材料参数,对于干燥曲线和浸润曲线分别取不同的值;θsat——饱和体积含水率;θirr——残余体积含水率.
为将扫描曲线严格地控制在2条边界曲线之间,将扫描曲线的含水率θ表示成θ1和 θ2的线性组合,即

基本模型的数值试验表明,出界问题主要取决于干湿转换时的体积含水率 θ0,为此取下述形式的组合系数:

式中 μ为控制扫描曲线的另一个参数.容易看出,通过这样的线性组合,扫描曲线必然会落在2条边界曲线之间,从而避免了扫描曲线出界的现象.
3 模型验证
a.用本文模型预测caribou粉土(土样的材料参数见表1).在脱湿扫描曲线中 β=4,μ=3;吸湿扫描曲线中β=3,μ=5.从图5可以看到,修正后的模型预测的扫描曲线不再出现初始阶段的直线段,也没有出界的现象,并且能较好地拟合试验点.

图5 模型预测caribou粉土与试验点比较Fig.5 Comparison of model predictions and experimental results for caribou silt loam
b.利用本文模型预测砂土(土样的材料参数参见表1).对于脱湿扫描曲线 β=4,μ=1.5;吸湿扫描曲线 β=4,μ=3.从图6可以看到,模型在预测砂土时,也可以克服上述直线段和出界2个问题.除了在吸湿过程起始点饱和度较高时,模型预测曲线与试验点存在着一些偏差,其余的试验点都能与模型较好地吻合.
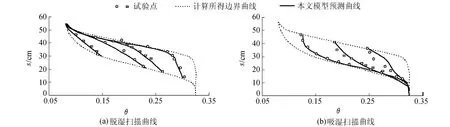
图6 模型预测砂土与试验点比较Fig.6 Comparison of model predictions and experimental results for sand

表1 土样材料参数Table 1 Material parameters of soil samples
4 结 语
本文根据Li的边界面建模思路,以基质吸力为自变量,以体积含水率为因变量,建立了一个可以考虑复杂干湿循环过程的土水特征曲线模型.本文模型中引入2个参数控制扫描曲线的形态,解决了Li模型可能出界的问题,并且能够较好地模拟不同土类的试验结果.
本文模型可以用于非饱和土力学、水力学耦合本构模型的建立;也可以用于非饱和土降雨入渗、心墙坝库水位下降等实际工程问题的求解.
[1]FREDLUNDDG ,RAHARDJOH.Soil mechanics for unsaturated soils[M].New York:John Wiley&Sons,1993:66-90.
[2]ALONSO E E,GENSA,JOSA A.A constitutive model for partially saturated soils[J].Géotechnique,1990,40(3):405-430.
[3]WHEELERS J,SIVAKUMARV.An elastic-plastic critical state framework for unsaturated soil[J].Géotechnique,1995,45(1):35-53.
[4]SHENG Dai-chao,GENSA,FREDLUNDDG ,et al.Unsaturated soils:from constitutivemodelling to numerical algorithms[J].Computers and Geotechnics,2008 ,35:810-814.
[5]NUTHM,LALOUI L.Effective stress concept in unsaturated soils:clarification and validation of a unified framework[J].International Journal for Numerical and Analytical Methods in Geomechanics,2008,32:771-801.
[6]LALOUI L,NUTH M.On the use of the generalized effective stress in the constitutive modeling of unsaturated soils[J].Computers and Geotechnics,2009 ,36:20-23.
[7]SUN De-an,MATSUOKA H,CUI Hong-bin,et al.Three-dimensional elastic-plastic model for unsaturated compacted soils with different initial densities[J].International Journal for Numerical and Analytical Methods in Geomechanics,2003,27:1079-1098.
[8]RUSSELL R,KHALILIN.A unified bounding surface plasticity model for unsaturated soils[J].International Journal for Numerical and Analytical Methods in Geomechanics,2006,30:181-212.
[9]GENSA,SANCHEZM ,SHENG Dai-chao.On constitutivemodeling of unsaturated soils[J].Acta Geotechnical,2006,1:137-147.
[10]HOULSBY G T.Thework input to an unsaturated granular material[J].Géotechnique,1997,47(1):193-196.
[11]ABAQUSTheory Manual Version 6.8[R].West Lafayette:Simulia Corp,2008:629-701.
[12]WEI Chang-fu,DEWOOLKARM M.Formulation of capillary with internal state variables[J].Water Resour Res,2006 ,42:W07405.
[13]LI Xiang-song.Modelling of hysteresis response for arbitrary wetting/drying paths[J].Computers and Geotechnics,2005,32:133-137.
[14]刘艳,赵成刚.土水特征曲线滞后模型的研究[J].岩土工程学报,2008,30(3):399-405.(LIU Yan,ZHAO Cheng-gang.Hysteresis model for soil-water characteristic curves[J].Chinese Journal of Geotechnical Engineering,2008,30(3):399-405.(in Chinese))
[15]FENGM,FREDLUNDDG.Hysteretic in fluenceassociated with thermal conductivity sensor measurements[C]//Proceedings from Theory to the Practice of Unsaturated Soil Mechanics:The 52nd Canadian Geotechnical Conference and Unsaturated Soil Group.Canada,Regina:RDGINA SASD,1999,14:214-220.
[16]TOPPG C.Soil water hysteresis in silt loam and clay loam soils[J].Water Resour Res,1971 ,7(4):914-920.
[17]POULOVASSILISA.A hysteresis of porewater in granular porous bodies[J].Soil Sci,1970,109(1):5-12.

