“数字信号处理”中循环卷积的简单计算方法

李昌利

(河海大学计算机与信息学院，江苏南京211100)

“信号与系统”课程中有一个非常重要的结论:离散线性时不变系统的响应为系统脉冲响应序列与输入序列的卷积(线性卷积)。“数字信号处理”课程中又定义了两个有限长序列的循环卷积运算。可以利用离散傅里叶变换的时域循环卷积性质来计算两个序列的线性卷积，而离散傅里叶变换可以通过快速傅里叶变换完成。通常的《数字信号处理》教材中讨论循环卷积时，给出了计算公式和计算实例，但都是从定义出发，计算过程复杂。本文从线性卷积的简单计算方法入手，利用线性卷积与循环卷积的关系，提出一个非常简便的计算循环卷积方法。

1 线性卷积和循环卷积及其关系

首先定义模运算。对任意整数m，m对N取模的运算符为:＜m＞N=m+lN，模运算定义为找一个整数l，使得0m+lNN－1。例如，＜23＞7=2，只要l=－3即可，又例如，＜-13＞7=1，只要l=2即可。

式中，N点循环卷积yC，N(n)定义域为0nN－1，长度为N。

对上述定义域内的x(n)和h(n)，在“信号与系统”课程中定义了两者的线性卷积为

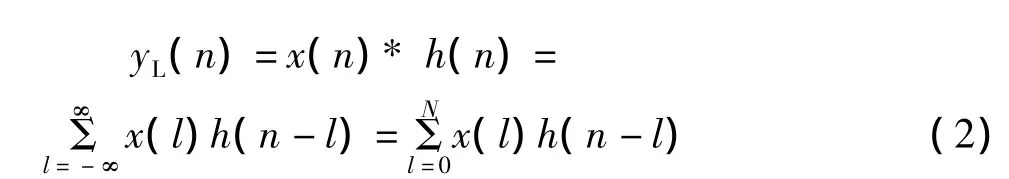
式中，yL(n)的定义域为0nM1+M2－2，有效长度为M1+M2－1。

［1] 指出循环卷积与线性卷积存在以下关系式:

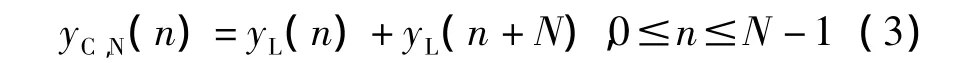
由此可知，当N≥M1+M2－1时，循环卷积与线性卷积相等;而当max(M1+M2)N＜M1+M2－1时，循环卷积与线性卷积不等。参考文献［2] 和［3] 详细证明了以上结论。

2 简单的循环卷积计算方法

我们首先简单介绍计算序列x(n)和序列h(n)线性卷积的序号和匹配法［4]，该法采用如下步骤。

(1)按序把x(n)和h(n)的序列值从左至右排列成两行。两个序列的第一个序列值排列时对齐，每个序列值占据一格;

(2)把x(n)的第一个序列值与h(n)的各个序列值依次相乘，把乘积结果按序从左至右排列，每个乘积结果占据一格;

(3)把x(n)的第二个序列值与h(n)的各个序列值依次相乘，把乘积结果按序从左至右排列，排列的起始位置较(2)右移一格;

(4)依据同样的方法，把x(n)的其它序列值与h(n)的各个序列值依次相乘，之后把所得的乘积结果依次排列，排列的起始位置依次右移一格;

(5)把同一列的乘积结果相加就是线性卷积结果，对应的序号n从左至右依次递增。

现在先计算5点循环卷积yC，4(n)。式(3)右边第二项yL(n+N)是由yL(n)左移5个单位形成的，得到如图1所示的中间结果yL(n+5)。因为循环卷积的定义域为0n4，所以只需考虑式(3)右边两项在0n4的部分，两项在0n4内的部分相加的最终结果如图2所示。

同理可得，6点循环卷积的最终结果如图3所示，7点循环卷积的中间结果如图4所示。

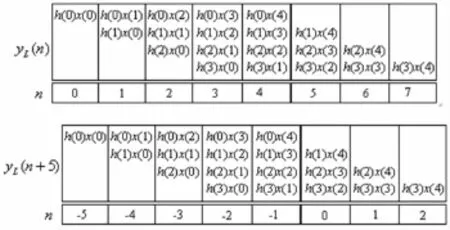
图1 计算5点循环卷积的中间结果

2计算5点循环卷积的最终结果

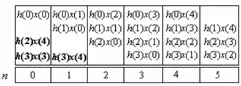
图3 计算6点循环卷积的最终结果

图4 计算7点循环卷积的最终结果

很容易验证，以上按列得到的各项恰与按式(1)计算得到的各项一致。事实上，也能以前述方法先计算两个序列的线性卷积yL(n)，再取(3)的右边，然后取两项相加结果在主值区间0nN－1的部分，此即序列的N点循环卷积yC，N(n)。

3 计算实例

设x(n)={2，1，0，1}和h(n)={2，3，0，1，2}，计算两者的6点循环卷积yC，6(n)。

先计算两个序列的线性卷积，得到的结果如图5所示。为了计算序列的6点循环卷积，将图5的结果整体左移6个单位，得到式(3)计算循环卷积的两项，中间结果如图6所示，图的底部标出了对应列的序号n。将前述结果在0n5的部分相加，得到的结果如图7所示，该图还给出了按列相加的结果，这就是最后的6点循环卷积结果yC，6(n)={5，10，3，4，8，2}，最后一行标示了对应的序号n。

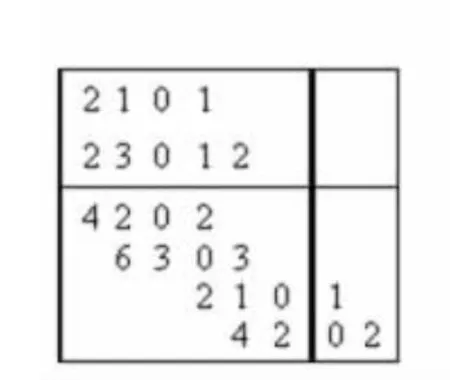
图5 线性卷积的计算

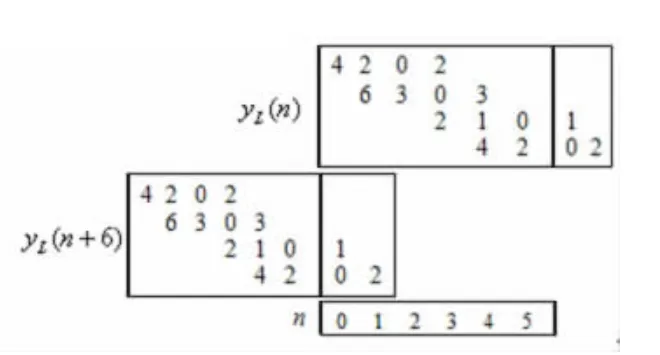
图6 循环卷积的中间结果

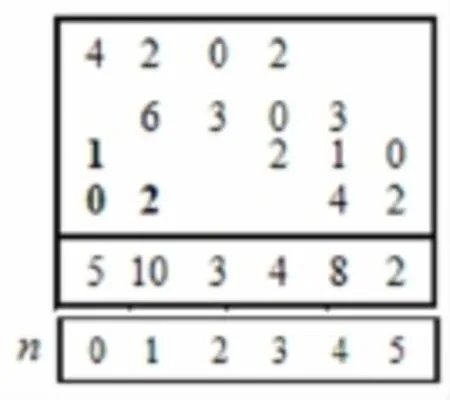
图7循环卷积的最终结果

4 结语

直接依据定义计算两个序列的循环卷积很繁琐。多数《数字信号处理》教材直接利用定义式计算循环卷积，由于定义式涉及到取模运算，所以计算过程很容易出错。分析表明。两个序列的循环卷积与线性卷积存在一个非常简单的关系式，而两个有限长序列的线性卷积很容易通过序号和匹配法计算，这样就得到本文提出的用于计算循环卷积的简单方法。文章涉及到的概念及公式是自包含的，本文通过具体分析和计算实例，详细地介绍了所提出的方法，便于读者阅读和参考。

参考文献:

［1] Vinay K.Ingle等著，刘树棠译.数字信号处理(MATLAB版)［M] .西安:西安交通大学出版社，2008

［2] 李昌利，霍冠英。“数字信号处理”中重叠保留法的证明［J] 。南京:电气电子教学学报.2011，33(6):31－32

［3] 于凤芹，张志刚，李昌利。数字信号处理简明教程［M] .北京:科学出版社，2011

［4] 李昌利。有限长序列卷积和求解法［M] 。南京:电气电子教学学报.2008，30(1):63－65