零阶保持器频率特性的仿真研究

王春侠

(陕西理工学院电气工程系，陕西汉中723003)

0 引言

由于零阶保持器具有最小相位滞后、结构简单和易于实现等特点，常用于闭环离散系统［1]。如图1所示，零阶保持器把采样时刻kT的采样值保持到(k十1)T时刻。即在时间t∈［kT，(k十1)T] 区间内，它的输出量一直保持为x(kT)这个值。依次类推，从而把离散信号恢复成了一个阶梯形的连续信号xh(t)。

离散信号经过零阶保持器解调后的阶梯形信号xh(t)的数学描述可以写为

对式(1)进行拉普拉斯变换得

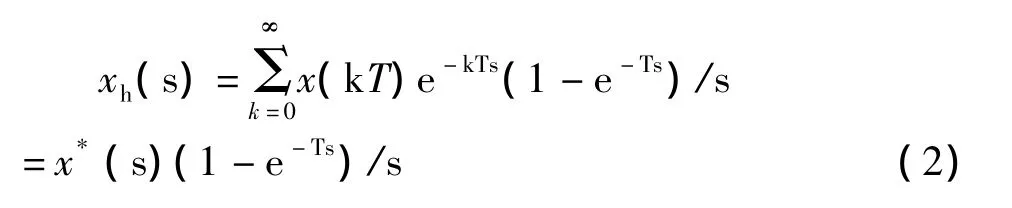
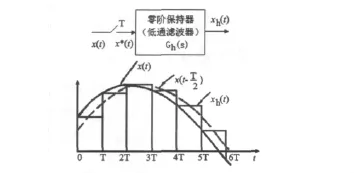
图1 采样和保持前后的信号

由上式可得零阶保持器的传递函数

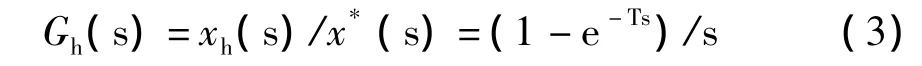
在笔者所见到的“自动控制原理”、“计算机控制技术”和“计算机控制系统”等课程的教材中，都是将s=jω代入式(3)得到零阶保持器的频率特性曲线，其中幅频特性|Gh(jω)|如图2(a)所示。相频特性有如图2(a)［1－4]、图(b)［5]和图(c)［7－11]所示的三种形式，其中图(a)和图(b)所示的相频特性是等价的。

笔者赞同图2(a)和图2(b)所示的相频特性曲线，认为图2(c)是错误的。本文基于Matlab软件，分别使用Padé近似法、直接计算法和分步计算法仿真研究零阶保持器的频率特性。

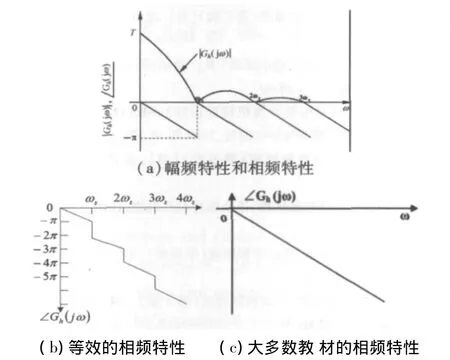
图2 现有教材零阶保持器的频率特性曲线

1 Padé近似法

Padé近似法的关键是在s域内对纯延迟环节的传递函数e－Ts进行n阶padé近似［6]，将其变成分子与分母同阶次的n次有理传递函数，其表达式为

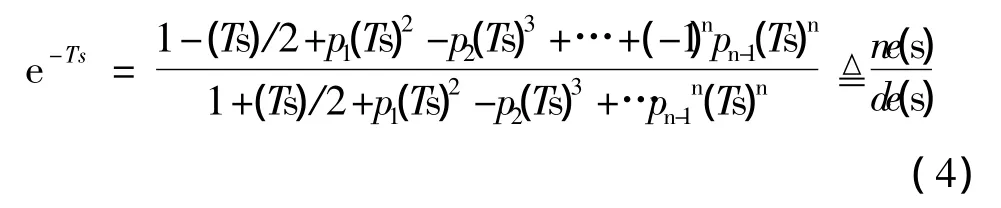
n值越大近似精度越高，一般取n=3～4就可以获得相当满意的精度［6]。将式(4)代入式(3)得到的有理传递函数形式:

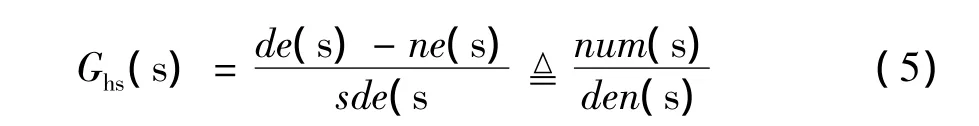
对式(5)按照有理传递函数的幅相频率特性曲线绘制方法可以绘制出零阶保持器的幅相频率特性曲线。取T=2s，将e－Ts近似成10阶有理多项式并绘制Gh(s)的幅相频率特性曲线由Matlab绘制的Gh(s)的幅相频率特性如图3所示。

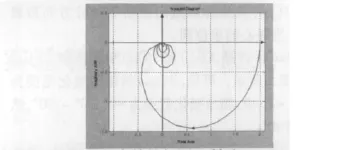
图3 T=2s时Gh(s)的幅相频率特性曲线

由图3可知，零阶保持器的初始幅值为T，初始相角为零。随着角频率ω从零变化到无穷，零阶保持器的幅值由T振荡衰减到零。零阶保持器总是存在相位滞后，最大滞后相角为π。这一结论与图2(a)一致。

2 直接计算法

根据传递函数与频率特性的关系，在式(3)中用jω代替s，得到零阶保持器的频率特性:

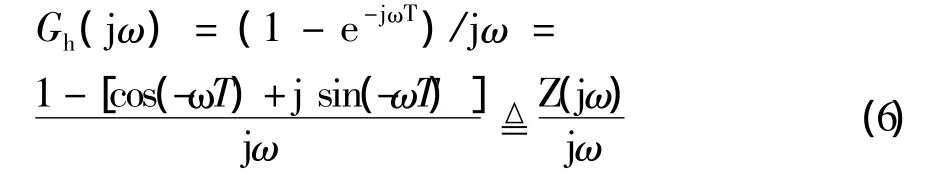
取T=2s(即ωs=π)，在ω≈0→ω=4ωs频率范围内，选步长为ωs/32，计算Gh(jω)的幅频特性A(ω)和相频特性D(ω)。通过Matlab绘制的Gh(s)的幅频特性和相频特性如图4所示，验证了图2(a)的正确性。

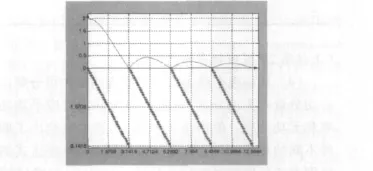
图4 T=2s时Gh(s)的幅频特性和相频特性曲线

3 分步计算法

式(6)还可以写成

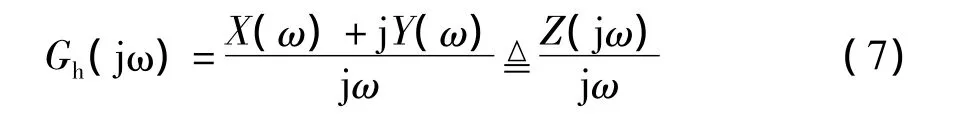
其中，X(ω)=1－cos(-ωT)，Y(ω)=-sin(-ωT)。

用Matlab计算X(ω)和Y(ω)后并绘制Z(jω)曲线，如图5所示。可见，Z(jω)的幅值变化范围为0(ω=0)～2～0，相角变化范围为90o～0o～-90o，然后跳变到90o。

图5 Z(jω)曲线

零阶保持器频率特性的极坐标形式为

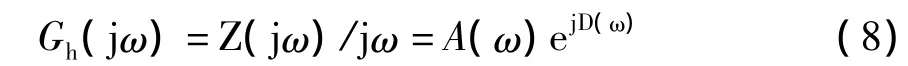
其中，A(ω)=|Z(jω)|/ω，D(ω)=∠Z(jω)－π/2。

用Matlab计算Gh(s)的幅频特性A(ω)和相频特性D(ω)，可见绘制的Gh(s)的幅频特性曲线和相频特性曲线同图5所示。该方法揭示了零阶保持器的相频特性反复变化范围为0o～-90o～-180o，然后跳变到0o的原由。

4 结语

我们采用以上三种方法从幅相频率特性、幅频和相频特性两个方面表明了零阶保持器的幅值随频率ω的增大而衰减;零阶保持器存在相位滞后，最大滞后相角为。其中第三种方法从本质上揭示了零阶保持器的相频特性为0～-π/2～-π，然后跳变到0反复变化的原因。期望本研究结果对零阶保持器的频率特性的相关教学有所帮助。

［1] 吴麒，王诗宓.自动控制原理·下册(第2版)［M] .北京:清华大学出版社，2006年.p.88-91

［2] 戴忠达，吕林.自动控制理论基础(第1版)［M] .北京:清华大学出版社，1991年.p.333-335

［3] 施保华，杨三青，周凤星.计算机控制技术［M] .武汉:华中科技大学出版社，2007年.p.15-16

［4] 孙炳达.自动控制原理(第二版)［M] .北京:机械工业出版社，2005年

［5] 冯勇.现代计算机控制系统［M] .哈尔滨:哈尔滨工业大学出版社.1997年.p.38-40

［6] 薛定宇.控制系统计算机辅助设计)—MATLAB语言及应用［M] .北京:清华大学出版社，1999年.P.176-178

［7] 胡寿松.自动控制原理(第五版)［M] .北京:科学出版社，2007年

［8] 李友善.自动控制原理(第3版)［M] .北京:国防工业出版社，2005年

［9] 王建辉，顾树生.自动控制原理(第四版)［M] .北京:冶金工业出版社，2007年

［10] 夏德钤，翁贻方.自动控制理论(第3版)［M] .北京:机械工业出版社，2007年

［11] 周雪琴.计算机控制系统［M] .西安:西北工业大学出版社。1998年