LonWorks工业网络测控系统时延控制
于建明
YU Jian-ming
(淮安信息职业技术学院,淮安 223003)
0 引言
随着微电子技术的发展、设备智能化水平的不断提高,人们对人与设备之间的信息交流和设备与设备之间的信息交流也提出了越来越高的需求。基于Web的LonWorks远程监控系统采用浏览器以简单友好的操作方式实现对生产现场数据的远程监视和控制,可以极大提高企业自动化水平,提高企业设备的维护管理水平。但对传送的信息量不大,但强调实时性的系统,其前向通道和反馈通道同时存在网络时延及其不确定性的问题,将会影响系统的动态性能。时延及其变化进一步增大时,还会导致系统不稳定。这一问题是阻碍远程控制采用因特网的主要原因。
为了解决这一问题,一些新的控制理论和方法已经被提出。Yang等[1]提出了如何系统地设计基于互联网的过程控制系统,并给出了该系统可能的结构基优缺点。Nillson采用随机最优控制的方法,在网络时延小于一个采样周期时,对具有独立随机时延和Markov特性延时的网络控制系统进行了研究等。然而,以上提高的方法在实际应用中也存在一些问题,如:使用最大的网络时延作为系统时延,可消除时延的随机性对系统的影响,但无形中增大了网络时延,增加了系统的响应时间。由于网络时延的随机性,很难用精确的数学模型描述出时延的分布规律,且由于Internet中普遍存在的丢包和包序颠倒等问题,也使得基于时延预估模型控制方法的应用受到了很大的限制。
在LonWorks远程控制系统中,由于网络时延的随机变化导致系统状态和参数等时刻发生变化,控制过程中会出现状态和参数的不确定性,系统很难达到最佳的控制效果。因此,有必要引入一些控制策略来补偿网络时延带来的影响。下面针对LonWorks在实现远程控制中存在的网络时延问题,提出一个初步的解决方案,缓解网络延迟对远程控制系统所产生的不良影响。
1 系统结构设计
1.1 网络时延分析
根据时延的产生过程和不同特性,可将其分为四个组成部分:发送处理时延τ1、等待时延τ2、传输时延τ3和接收处理时延τ4。其中τ1和τ2在源节点产生,τ4在目标节点产生,τ3是信息发送时间与在信道传播时间之和。网络时延可表达为

时延对系统性能的影响,主要是由两个部分引起一是控制器得到的反馈信号不是当前系统输出,而是经过了时延;二是控制量到执行器又经过了时延。而发送处理时延、等待时延及接收处理时延可以通过软件设置心跳/最大接收时间、时限阈值,最小差值等属性,减小网络变量更新时所造成的信息延时。将两者综合起来分析,相当于系统输出在当前采样周期被延时了,本文重点解决的也就是信号在网络传输过程中所产生的时延问题。换个角度来看,就是发生了采样抖动,如果对系统时延不加补偿,控制器接收到并据以采取控制动作的是被延迟了的采样信号,不能真实反映当前时刻的被控对象的状态,因而产生的控制动作也是滞后的,这将导致系统性能变差和不稳定。
1.2 网络时延的测量
采用BP神经网络预测网络时延,神经网络最大的优点就是具有可以逼近任意的非线性的能力,理论上具有偏差和至少一个S型隐含层加上一个线性输出层就可以逼近任意非线性,据此决定系统采用带有一个隐含层的三层BP神经网络来预测延时。神经网络输入层的神经元的个数取决于取得的历史延时信息的个数,由一个滑动窗口根据网络延时的状态调整。中间层神经元的个数依据金字塔结构采取和输入层相等的数目,如图1所示。

图1 预测延时采用的BP神经网络结构
在采用神经网络预测延时时提出了“先预测,后验证”的思想,即先依据已经获取的从前一段时间内的延时信息训练神经网络,确定神经网络的权值,然后根据这些权值预测网络当前时刻网络的延时状况,在补偿器进行延时补偿。当获得该时刻对应的网络延时的实际值后,比较实际值和预测值,如果预测误差小于许可范围,认为网络状况还没有发生剧烈的变化,继续使用该权值预测延时,而无需重新训练权值。否则,必须重新训练权值,训练神经网络使用的信号为上一时刻网络的真实延时。
如果当前延时预测误差满足系统性能容忍的误差要求,则使用当前神经网络的权值预测延时,此为正向处理。在给定输入Ii、输入层到中间层的连接权值Wji以及中间层的偏置值θj之后,可以求出中间层单元j的输出:
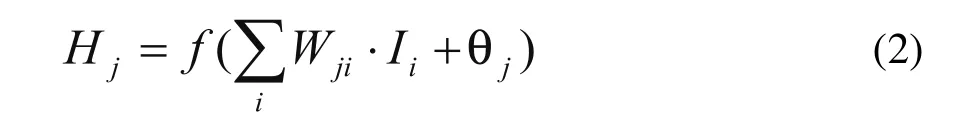
其中f是sigmoid函数,即
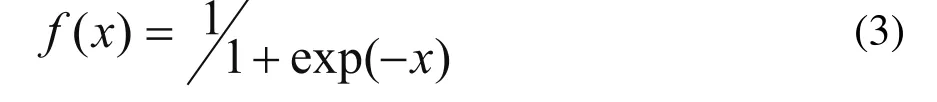
用中间层的输出Hj、中间层到输出层的连接权值Vkj以及输出层单元k的偏置值,可以求出输出层单元的输出Ok:

如果预测误差超过了系统的容忍误差要求,就要对神经网络的权值进行修正,重新进行权值训练,此为反向处理。误差修正采用BP(反向运算)算法,其中Vkj、、Wji和θj的修正公式分别为:

系统实现时需进一步修正基本的BP神经网络预测算法,将k时刻的神经网络输出值减去k-1时刻的预测误差作为k时刻互联网延时预测值,修正流程图如图2所示。

图2 BP神经网络预测算法修正流程图
1.3 网络时延补偿
前向和反馈通道由因特网来传递控制信息和反馈信息,网络传输存在时延,被控对象的运动状态不能及时反馈和输入信号进行比较或控制信号不能及时加到被控对象上,系统处于非正常状态,系统的性能降低,甚至不能正常工作。为此,在获得网络时延值后,需要在系统中接入补偿器,以消除网络时延的影响。时延补偿思路如图3所示。
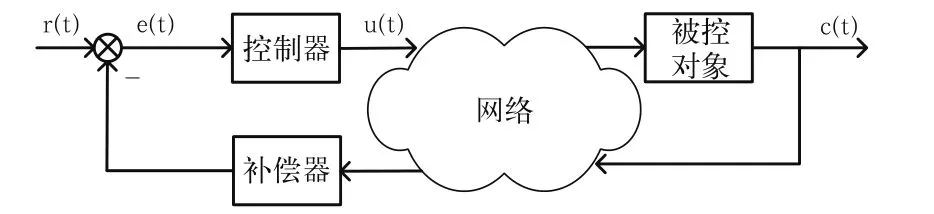
图3 时延补偿思路
1.3.1 PID控制器
根据网络控制特点,引入PID控制器,在对模型精确已知的控制对象,在参数选择恰当的情况下可以有效地减少超调量和响应时间,使系统具有较好的鲁棒性。PID控制器产生的控制信号
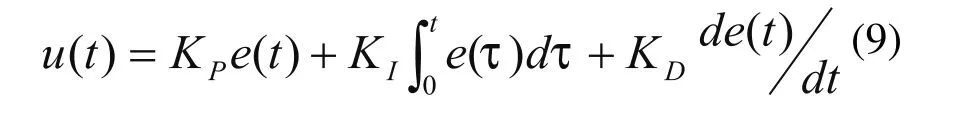
式中e(t)为误差信号,KP为比例增益,KI为积分增益,KD为微分增益。对该式进行拉普拉斯变换后得到PID控制器的传递函数

1.3.2 Smith预估补偿器
为了改善滞后系统的控制品质,1957年O.J.M.Smith提出了一种以模型为基础的预估器补偿控制的方法[3]。其设计思想为:预先估计过程在基本扰动作用下的动态响应,然后由预估器进行动态补偿,试图使被延迟的被控量超前反馈到控制器,使控制器提前动作,从而大大降低了超调量,并加速调节过程[4]。在此利用Smith预估器对纯滞后系统的补偿控制原理,将网络时延引入到Smtih预估器,对系统进行动态补偿控制。远程控制系统如图4所示。

图4 带有时延预估补偿控制的系统结构图
该项研究中为实验所用的直流电机的传递函数。Smith预估器的传递函数为,其中为被控对象传递函数,为t时刻网络时延预测值。由于目前互联网中路由器多是采用动态路由协议依据互联网负载状况来选择信息的传递路由,因此互联网负载的实时变化,造成信息的传递路由动态变化,从而导致信息传递延时具有不确定性。如果补偿器中使用的延时信息不能够随着互联网实际时延的变化而变化,那么系统的性能依旧不能得到保证。
2 系统仿真试验
2.1 BP网络设计
MATLAB环境下的神经网络工具箱是以人工神经理论为基础,利用MATLAB语言构造出许多典型网络的激活函数、各种典型的修正网络权值规则和网络的训练过程[2]。这样网络的设计可根据自己的需要调用工具箱中有关神经网络设计与训练的程序,避免繁琐的变成过程,从而大大提高效率和质量。
此外,还可应用图形用户界面(GUI)来进行神经网络设计,双击Neural Network toolbox中的NNTool,即可进入神经网络设计主界面,如图5所示。和上面是用函数来创建网络一样,需要设计一些参数,如网络类型、名称、输入向量的最大值和最小值、网络的层数等。
图5 神经网络设计主界面
在采用神经网络预测延时时提出了“先预测,后验证”的思想,即先依据已经获取的从前一段时间内的延时信息训练神经网络,确定神经网络的权值,然后根据这些权值预测网络当前时刻网络的延时状况,在补偿器进行延时补偿。当获得该时刻对应的网络延时的实际值后,比较实际值和预测值,如果预测误差小于许可范围,认为网络状况还没有发生剧烈的变化,继续使用该权值预测延时,而无需重新训练权值。否则,必须重新训练权值,训练神经网络使用的信号为上一时刻网络的真实延时。
2.2 训练数据导入
要对BP网络进行训练,必须有训练样本。对训练样本数据的获得,MATLAB提供了一些方法[2]。根据实际情况,对于Internet与控制网络的连接,采用购买的动态测量Internet点对点网络时延软件Get Delay,并使用与其配套的软件即可实现网络时延的测量以及数据格式的转换,然后用load函数将数据读取到MATLAB中。
2.3 仿真试验
具体实现时,还仔细考虑了通讯协议和工作方式的选择问题。由于在基于互联网的远程控制系统中控制信息和反馈信息的产生具有频率高、数据量小的特点,因此如果选择TCP协议,就必须屏蔽TCP协议提供的“尽力而为(Best Effort)”功能,以便控制信息和反馈信息及时发送和接收。此外,选择TCP协议网络开销比较大,不仅体现在其三次握手的确认机制上,还体现在其报文头部相比于数据要大。
首先,采用点对点控制结构。这时系统中信号的传递不存在时延,通过仿真计算得到系统阶跃响应曲线如图6所示。

图6 采用点对点结构的单位阶跃响应
图中曲线1为输入单位阶跃信号,曲线2为系统阶跃响应,可以看到这时系统具有满意的响应特性。
接着,采用如前面讨论的网络控制系统。网络采用淮安信息学院与淮阴工学院之间的Internet,网络中的数据由淮安信息学院S2实验楼主机发出,首先转发到淮阴工学院的路由器,然后再转发回淮安信息学院主机,发送流量为91.2kb/s。在网络存在时延的情况下,采用不同的控制器方式进行试验,如图7所示。将图中虚线框中的结构去掉后,为第一种控制方式,即PID控制。加入smith预估器后为第二种控制方式,PID加smith预估控制,由于加入smith预估器其中牵涉到网络时延参数的确定。由于没有加入时延预估算法,只能根据所测得的近期网络时延值确定一个适中量。加入BP网络预测时延后为第三种控制方式。系统阶跃响应曲线如图8所示。

图7 控制方式方框图

图8 不同控制器条件下的阶跃响应
3 仿真结果分析
图8中曲线1为控制信号,曲线2为PID控制器作用下的阶跃响应曲线,曲线3为采用PID控制器和smith预估器作用下的阶跃响应曲线,曲线4为采用PID控制器和smith预估器作用并采用BP网络预测时延的阶跃响应曲线,分析试验结果,得到如下结论:
1)稳定性得到保持。采用不同控制器作用的远程控制系统均能维持控制系统的稳定性,与点对点结构时的响应曲线进行比较,最后都能到达稳定状态。由于远程控制系统运行时存在时延,将会引起系统输出量的振荡,但这种振荡随着时间的推移而逐渐减小乃至消失,系统最终是稳定的。
2)超调量得到降低。超调量指的是响应曲线对稳态值的超出量与稳态值之比,其中比较关注的是最大超出量的大小,亦即最大超调量。从点对点结构时的响应曲线,可以看出系统超调量很小;在有时延的情况下,曲线2到曲线4的超调量依次降低,说明加入了控制器之后,远程控制系统的性能得到了改善。而且从曲线3和曲线4可以明显看到,加入时延预测后得到的响应曲线4超调量较小。
3)调节时间得到减少。调节时间指响应曲线进入并不再超出稳态值附近规定误差带的最小时间,在有时延的情况下,曲线2和曲线3的调节时间较长,而且比较接近,曲线4表现出的动态响应特性接近于点对点结构时的响应特性,调节时间与曲线2和曲线3相比减小了很多。
4 结束语
从以上分析可以得到这样的结论,采用适当的网络时延补偿控制器,对互联网中的不确定性时延进行正确预测,可以有效地解决LonWorks远程控制系统在Internet环境下由于网络延迟造成的动作滞后等问题,不仅能维持控制系统得稳定性,而且明显降低了超调量,减小了调节时间,表现出良好的动态性能,使得远程被控系统在接近稳态时的控制品质得到了改善,加快了系统达到稳态的速度。
[1]Yang S H,Chen X,Alty J.Design issues and implementation of internet-based process control system[J].Control Engineering Practice.2003(6):709-720.
[2]黄忠霖.控制系统MATLAB计算及仿真[M].北京:国防工业出版社.2001:12-50.
[3]任长清,吴平东等.基于互联网的液压远程控制系统的延时预测算法的研究[J].北京理工大学学报.2002(5):14-19.
[4]王小平.遗传算法理论应用于软件实现[M].西安.西安交通大学出版社.2002.
[5]李颖宏,李正煦.基于LonWorks的智能PID控制器的设计[J].仪器仪表学报.2005(4):419-421.

