SCS模型在黄河中游次洪模拟中的分布式应用

李 丽,王加虎,郝振纯,刘文斌

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.黑龙江省水文局,黑龙江 哈尔滨 150001)

流域地表特性的不均一性和气象条件的时空变化都会对水文过程产生影响,并影响到水文模型的模拟结果.近些年来,出现了大量以GIS和遥感等技术手段为基础考虑下垫面的空间分布不均一性对水文过程产生影响的研究.研究内容涉及蒸散发[1]、植被截留[2]、下渗[3]、径流量[4]和汇流过程[5]等多个方面.分布式水文模型中对下垫面分布不均一性的考虑也主要集中在地形、地表覆被/土地利用方式和土壤类型几个方面.其中地形的影响主要体现在初始土壤含水量和流域汇流特性的空间分布上,地表覆被的影响主要在蒸散发和植被截留计算中考虑,而土地利用方式和土壤类型的影响则更多地体现在下渗和产流量的计算中.基于以上各方面的研究,出现了一些以这些物理理论为基础的分布式水文模型,如SHE模型[6]、SWAT模型[7-8]等.但由于资料、技术等因素的制约,这些以物理机制为基础的分布式水文模型的应用也受到了相当程度的限制.因此,在基于物理基础的分布式水文模型尚未发展成熟和现有科学技术水平的制约下,要在水文模型中考虑下垫面时空变化对产汇流特性的影响,还需要走一条介于物理机制和集总式水文模型之间的道路.为考虑地表覆被类型和土壤类型的空间分布对水文过程的影响,笔者选择基于植被和土壤类型确定参数的SCS模型来进行空间分布式的流域水文模拟研究.

1 集总式SCS模型简介

SCS模型最初是由美国土壤保持局(U.S.Soil Conservation Service)针对小流域洪水设计而开发的[9],是在土壤保持工程和防洪工程的设计中发展起来的径流和洪峰流量估算方法,后来又演变出许多不同的形式.它只有一个参数:曲线数值(curve number,通常称之为CN值),该参数随土壤、地表覆被、土地利用种类及方式而不同,在不同的洪水事件中,CN的取值还受前期土壤含水量的影响.因此,SCS模型又称SCS-CN法,该模型的应用重点集中在CN值的选取上,模型制作者以美国的自然地理状况和水文气象条件为基础,经过大量的数理统计和成因分析得到了一套完整的根据下垫面条件确定CN值的方法,并给出了不同条件下相应的CN参考值.由于SCS方法具有广泛的资料基础,并在应用中考虑了物理特性,在美国和欧洲一些国家得到了较为广泛的应用.

SCS模型的产流公式为

式中:R——产流深;I——降水;S——最大潜在降水损失,即降水与径流之间可能的最大差值;Ia——降水的初期损失,包括地面洼地蓄水、植物截流、下渗和蒸发.初期损失项Ia是变化的,表现前期降水对此刻降水初始损失的影响,模型制作者根据美国农业集水区的资料和经验公式近似确定

这种近似关系,在不同情形下可能发生改变,如在城市区不透水面和透水面的组合可能减小初期损失,而如果不透水面是一个洼地,可以蓄积一部分径流,就有可能增加初期损失.如果不用该经验关系,就必须根据降雨-径流资料对每一种下垫面条件,建立新的 Ia与S或CN的关系.

S通过径流曲线数CN与土壤和流域覆被条件建立关系,计算公式为

式中NC为径流曲线数CN.

NC表示不同条件对产流的影响,确定NC的主要因素是土壤的水文分组、覆被类型和覆盖情况、水文条件以及前期径流条件.确定其值需要覆被类型和覆被情况、土壤以及前期径流条件3组数据,不同的组合对应不同的NC[10-11].

SCS模型的产流计算方程不包含时间因素,不能考虑降雨历时或强度的作用,因此由以上方法直接计算的径流量为1场降水的径流总量.当将该产流公式用于估算1次暴雨的逐时径流过程时,需用每个时段末的累积降雨求相应的累积径流量,相邻时段的累积径流量相减,就可得每个时段的径流量[12].

SCS方法中,洪峰流量和峰现时间由净雨历时D,按三角形过程线由经验公式近似推求[12].在汇流计算中,模型制作者采用一条统一的无因次单位线来计算径流输出过程,该无因次单位线由洪峰流量和峰现时间推导[10].

2 分布式SCS模型的建立

SCS模型多用于计算小流域设计洪水,其参数CN虽然随下垫面状况、前期水文条件等的变化而取值不同,但在传统的流域计算中多对不同下垫面的CN值加权平均,计算流域平均的CN值[12],进而进行流域的径流量和流域出口过程线估算.然而,对于分布式水文模拟而言,地表覆被、土壤、前期水文条件等的空间分布不均匀性将直接表现在径流量的空间分布上,如果利用SCS模型进行产流量计算,则可以直接应用GIS和RS所提供的下垫面资料来考虑下垫面的空间分布特性.

但是,SCS模型是在美国各种下垫面条件下开发制作的,如果移用到我国,必然存在一个参数的重新率定和经验公式的调整问题.关于SCS模型的移用,国内外已有不少研究.其中有一种方法是放弃CN值,直接确定初损和流域当时的可能滞留量,并代入径流量计算公式中参与计算[13-14],但对于分布式水文模拟和实测资料不足的地区这种方法并不适用,也失去了SCS模型本身的优势.

为在分布式水文模拟中应用SCS模型,并使其不失考虑下垫面分类的优势,只有保持CN的作用,对模型参数进行重新确定.移用中参数的确定方法有2类:一是针对各地区的特点和不同的地表覆被、土壤组合重新率定CN值[15-16].如果将其应用于集总式模型,可以将CN作为流域平均参数进行调试和率定;但若将其应用到分布式水文模拟中,则需要寻求各种具有单一下垫面组合的小流域,根据实测径流量反推CN值,由于下垫面特征的空间变异性,要在天然流域中寻找这样的小流域率定参数并大范围移用并非易事.另外一种就是对径流量计算公式进行修正[17-18],包括对I a和R的修正.对初损的修正方法往往是将I a=0.2S修改为Ia=mS,m随着不同地区的自然地理情况和水文条件的差异而变化,可通过参数率定确定其值;对径流量的修正则通过一个相关关系实现,将SCS模型计算的数据与实测数据之间的比值作为参数,采用一次反馈的方法,找出该比值与降雨量的关系,从而对应用SCS方法产生的误差进行修正.

参数跨地区移用的根本问题在于下垫面和气候条件的变化,而在SCS模型中能够表现这些因素影响的关键之处在于参数CN和降雨初损I a,CN表现了地表覆被、土壤等下垫面情况的一般产流条件,而初损I a与最大潜在损失的比例m更多地体现了下垫面的产流速度,如适用超渗产流模式的地区的初损比例可能要小于适用蓄满产流的地区.将适用于美国地理状况和气候条件的SCS模型应用到我国,必须对这2个参数进行调整.同时为了能够反映径流量空间变化和最大限度地利用已有条件和研究成果,本文引入2个参数对SCS模型的径流量计算方法进行调整,它们就是初损比例m和CN的系统偏差系数k.那么,径流量的计算公式就变为

这2个参数可在模型建立过程中通过率定参数来确定.

SCS模型采用无因次单位线进行汇流计算,是针对流域计算而设计的,在以栅格为基本单元的分布式汇流计算中并不一定适用.对于尺度较大的栅格可以将每个基本单元都作为汇流单元求其单位线、计算出流过程,全流域的汇流过程则根据这些基本单元的出流过程和单元间的上下游关系,采用分布式的汇流架构计算;但对于尺度较小的栅格,根据SCS汇流方法计算每个栅格的单位线就不合适了,分布式的汇流需求也使单位线不能发挥作用.但无论栅格尺度大小,栅格间的分布式汇流演算都是必不可少的.因此舍弃SCS模型本身的汇流计算方法,采用分布式的概念性汇流方法[19]:河道和水库相结合的方法,在用河道(即水流路径上的汇流时间)描述洪水的平移过程的同时,用线性水库模拟洪水汇集过程中的坦化现象.

3 应用实例

选取黄河流域三门峡—小浪底区间上八里胡同水文站所控制的小流域为研究对象(图1),以上述方法建立分布式水文模型.研究区域基本上为土石山区,特点是地势陡峻、土层较薄、植被良好、径流系数较大,利于产流.研究中所用到的资料包括:八里胡同站的次洪摘录资料(共5场洪水);区域内雨量站的降水摘录资料;30″空间分辨率的DEM以及区域内的植被和土壤类型分布图.

为避免针对不同的植被和土壤类型重新率定CN值,研究中首先根据区域内的植被和土壤类型确定初始的CN值(图2(a)所示为CN值的空间分布),然后通过CN的系统偏差系数k来对研究区域内的CN值进行整体调整,即避免了利用大量资料重新率定CN值,又能考虑下垫面对径流量空间分布的影响.以19760821次洪水为例,图2(b)所示为利用泰森多边形所求得的区域内降水量的空间分布,图2(c)所示则为利用上述模型计算出的径流深的空间分布.由图2可见,径流深的空间分布不仅体现了降水量的空间分布不均匀性,也在一定程度上表现了下垫面的空间变异性对径流量计算的影响.

图1 研究区域位置(深色区域)Fig.1 Location of study area(highlighted by dark color)

图2 19760821次洪水的计算结果Fig.2 Calculated results for flood event 19760821

此外,由于参数CN与前期土壤含水量紧密相关,原SCS-CN法中根据前期降水将前期土壤湿度划分为干、中、湿3类,3种情形下的CN值存在一定的相关关系.但将该模型移用到研究区域时,由于气候和地理条件的变化,这个判断土壤干湿的标准也必定会发生变化.本文将前期土壤湿度对径流量的影响表现在CN的系统偏差修正系数k上.对该参数的率定结果进行分析(如表1所示,表中k值所对应的径流总量相对误差小于±1%),发现该参数与前期降雨量存在一定的相关性,可根据前期降水量对k初步确定3种取值,分别对应于干、中、湿3种情况,其取值范围应该分别在1.15,1.44,1.56附近.以这3种取值分别计算上述洪水的径流量(表2),径流量相对误差仍在许可范围之内(＜20%).

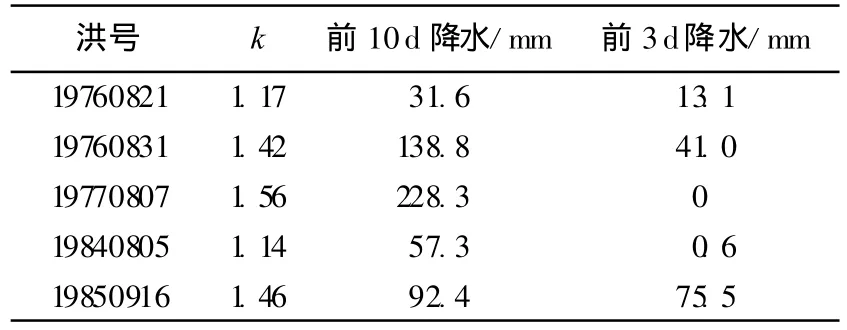
表1 对应5场洪水的k值和前期降水Table 1 k values and antecedent precipitations in five flood events

表2 确定k值时的计算径流量误差Table 2 Relative errors of calculated runoff when determining k values

以上分析说明,系统偏差修正系数k与原文献中CN值随前期土湿情况的变化存在相似性,即亦可在对历史洪水进行分析的基础上,根据前期降水量或前期土壤含水量估算其值,为洪水预报服务.

4 结 论

分布式水文模拟需要考虑地表覆被、土地利用、土壤、地形等下垫面条件的空间变化,传统的概念性水文模型不易达到这样的要求,而以物理机制为基础的分布式物理模型则需要大量的资料和复杂的计算,在大流域应用时其精度也受到很大的限制.传统的SCS模型虽然是经验性集总式水文模型,但是考虑了土地利用、土壤分类等对水文循环的影响,并且具有成熟的参数体系.这是其他传统水文模型所不具备的巨大优势,因此可将SCS模型的计算方法和参数进行合理调整,用于分布式水文计算.本文以原有确定CN值的方法为基础,通过引入CN值系统偏差修正系数k和降水初期损失占最大潜在损失的比例m这2个系数,来考虑研究区域与模型建立区之间的下垫面特性和气候特性的差异,对径流量计算方法进行了合理的修正,达到参数移用的目的,又不失SCS模型自身的优势.

由于资料的限制,本文还没有建立准确的前期土壤湿度的判断标准,不同前期土壤湿度下的k值也缺乏足够的算例和证明等.但是仅有的算例也足以说明本文方法是合理的,具有进一步研究和在分布式水文模拟中应用的价值.

[1]DUNNSM,MACKAY R.Spatial variation in evapotranspiration and the influence of land use on catchment hydrology[J].Journal of Hydrology,1995,171:49-73.

[2]王中根,郑红星,刘昌明,等.黄河典型流域分布式水文模型及应用研究[J].中国科学:E辑 技术科学,2004,34(增刊):49-59.(WANG Zhong-gen,ZHENG Hong-xing,LIU Chang-min,et al.Representative distributed hydrological model of Yellow River and a case study[J].Sciencein China:Ser E Technological Science,2004,34(Sup):49-59.(in Chinese))

[3]REGAB R,COOPER J D.Variability of unsaturated zone water transport parameters:implication for hydrological modeling:Ⅰ.in situ measurements[J].Journal of Hydrology,1993,148:109-131.

[4]雷孝章,王金锡,赵文谦.森林对降雨径流的调蓄转化规律研究[J].四川林业科技,2000,21(2):7-12.(LEI Xiao-zhang,WANG Jin-xi,ZHAO Wen-qian.Research on the regulation and transfer rules of forestto precipitation-runoff[J].Journal of Sichuan Forestry Science and Technology,2000,21(2):7-12.(in Chinese))

[5]MOUSSA R,VOLTZ M,ANDRIEUX P.Effects of the spatial organization of agricultural management on the hydrological behavior of a farmed catchment during flood[J].Hydrological Processes,2002,16:393-412.

[6]BATHURST JC,WICKS JM,O'CONNELL P E.The SHE/SHESED basin scale water flow and sediment transport modeling system[M]//SINGH VP.Computer models of watershed hydrology.Colorado,USA:Water Resources Publication,1995:563-594.

[7]NEITSCH SL,ARNOLD JG,KINIRY JR,et al.Soil and water assessment tool theoretical documentation,TWRI Report TR-191[R].Austin,Texas,USA:Texas Water Resources Institute,College Station,2002.

[8]ECKHARDT K,HAVERKAMPS,FOHRERN,et al.A version of SWAT99.2modified for application to low mountain range catchments[J].Physics and Chemistry of the Earth,2002,27:641-644.

[9]PONCE V M,HAWKINS RH.Runoff curve number:has it reached maturity?[J].Journal of Hydrologic Engineering,ASCE,1996,1(1):11-19.

[10]MAIDMENT D R.水文学手册[K].张建云,李纪生,朱元生生,等,译.北京:科学出版社,2002:156-196.

[11]SCHWAB G O,FREVERT RK,TALCOTTW,et al.Soil and water conservation engineering[M].3rd ed.New York:John Wiley&Sons,1981:69-91.

[12]CAMORANI G,CASTELLARIN A,BRATH A.Effects of land-use changes on thehydrologic responseof reclamation systems[J].Physics and Chemistry of the Earth,2005,30:561-574.

[13]张秀英,孟飞,丁宁.SCS模型在干旱半干旱区小流域径流估算中的应用[J].水土保持研究,2003,10(4):172-175.(ZHANG Xiu-ying,MENG Fei,DING Ning.Application of SCSmodel to estimating the quantity of runoff of small watershed in semi-arid or arid region[J].Research of Soil and Water Conservation,2003,10(4):172-175.(in Chinese))

[14]王建,丁永建,刘时银.高寒草地春节积雪融水和雨水混合补给径流模拟[J].干旱区资源与环境,2006,12(1):88-92.(WANG Jian,DING Yong-jian,LIUShi-yin.The simulation of snow melting water and rainwater supply to runoff in cold grass region in spring[J].Journal of Arid Land Resources and Environment,2006,12(1):88-92.(in Chinese))

[15]PAYRAUDEAUS,TOURNOUDM G,CERNESSON F.Sensitivity of effective rainfall amount to land use description using GIS tool:case of a small Mediterranean catchment[J].Physics and Chemistry of the Earth,2003,28:255-262.

[16]王宏,张智忠,马勇.SCS模型在削洪减沙效益计算中的应用[J].水土保持科技情报,1995(3):40-42.(WANG Hong,ZHANG Zhi-zhong,MA Yong.Application of SCSmodel in the estimating of flood and sediment control[J].Scientific and Technical Informationof Soil and Water Conservation,1995(3):40-42.(in Chinese))

[17]王白陆.SCS产流模型的改进[J].人民黄河,2005,27(5):24-26.(WANG Bai-lu.Improvement of rainfall-runoff generation part in SCSmodel[J].Yellow River,2005,27(5):24-26.(in Chinese))

[18]贺宝根,陈春根,周乃晟.城市化地区径流系数及其应用[J].上海环境科学,2003,22(7):472-476.(HE Bao-gen,CHEN Chungen,ZHOU Nai-sheng.Urbanized arearunoff coefficient and its application[J].Shanghai Environmental Sciences,2003,22(7):472-476.(in Chinese))

[19]李丽,郝振纯,王加虎.一个以DEM为基础的分布式水文模型[J].水电能源科学,2004,22(4):5-7.(LI Li,HAO Zhen-chun,WANG Jia-hu.Distributed hydrologic model based on DEM[J].Hydroelectric Energy,2004,22(4):5-7.(in Chinese))