新安江模型在乌江独木河流域的应用与改进

郝庆庆,陈 喜,2

(1.河海大学水文水资源学院,江苏南京 210098;2.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098)

新安江模型[1-2]是一个分单元、分水源、分阶段,具有分布参数的完整的概念性降雨径流模型,适用于湿润与半湿润地区,具有概念清晰、结构合理、调参方便和计算精度较高等优点.模拟计算主要分为蒸散发、产流、分水源和汇流4个阶段.其中:蒸散发计算采用3层蒸散发模型;产流计算采用蓄满产流模型;径流划分为地表径流、壤中流和地下径流3种水源,径流划分采用了自由水蓄水库法;汇流计算中,地表径流汇流计算采用无因次单位线法,壤中流和地下径流汇流计算采用线性水库法,河道汇流计算则采用马斯京根分段连续演算法[2].

本文的研究对象独木河流域地处西南喀斯特地区.该区为连片裸露碳酸岩面积最大和生态最脆弱的地区[3-4],虽然降水较多,但时空分布不均且下垫面情况复杂.根据岩溶地区独特的水文地质特性[5]以及三水源新安江模型应用于岩溶地区的模拟结果分析,笔者提出了改进新安江模型的3种设想[6],并验证了第1种改进方法.

1 模型的应用

研究区为贵州省内乌江流域的支流——独木河流域,面积1485km2.该流域内共有下湾、昌明和六广3个站点.

1.1 日模拟

采用独木河流域1973—1979年的水文资料率定日模参数,1980—1983年的水文资料检验日模参数,缺失的部分资料移用邻近水文特征相似站点的来代替.日模参数[7]的率定顺序为蒸散发折算系数K→表层土自由水蓄水容量SM和表层土自由水蓄水库对地下水的出流系数KG与表层土自由水蓄水库对壤中流的出流系数KI的比值KG/KI→地下径流的消退系数CG→壤中流的消退系数CI.率定蒸散发折算系数K时以径流深绝对误差为目标函数[8],计算公式为

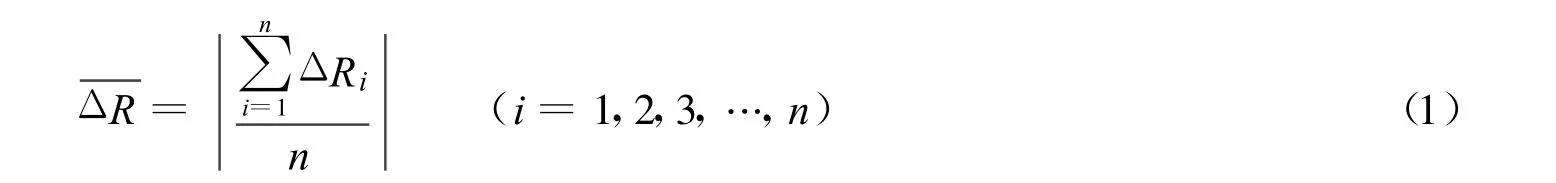
式中:ΔRi——第 i年径流深的绝对误差——n年径流深绝对误差的平均值;n——资料的年数.

率定其他参数时[9],为减少洪水高水部分误差的作用,突出低水部分的作用,以误差的对数为目标函数,通过使流量过程线对数误差绝对值的平均值最小的方法来优选参数.

式中:Q(j)——实测日平均流量;Q′(j)——计算日平均流量;f(i)——第 i年的流量过程线对数误差的绝对值——n年流量过程线对数误差绝对值的平均值.

计算结果见表1和表2.

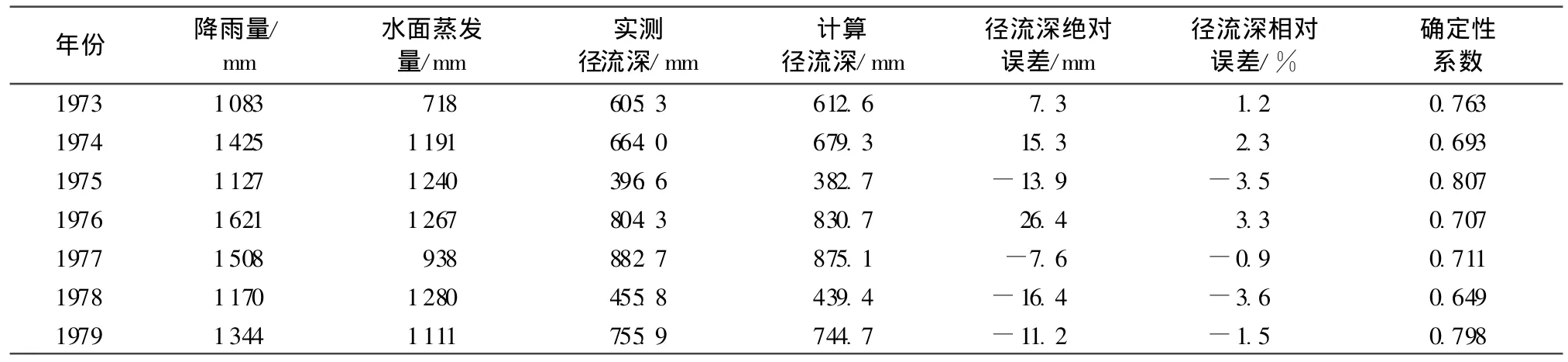
表1 率定年份日模模拟结果Table 1 Daily simulation results in calibration years

表2 检验年份日模模拟结果Table 2 Daily simulation results in examining years

分析表1和表2结果可知:(a)率定得到的日模参数对多年来说是最优的,对于有些年份的模拟结果很好,而对于另外一些年份的模拟结果相对较差;(b)新安江模型没有考虑随着时间推移下垫面的变化以及人类活动的影响,是造成模拟误差的一个原因;(c)在极值处的预报结果相对较差,计算峰值基本都小于实测峰值,这可能是流域下垫面特性、模型概化、参数率定以及水文资料等因素综合作用及相互影响的结果;(d)个别年份(如1983年)出现计算峰值明显高于实测峰值的现象,这可能是抽水等人为因素造成的;(e)所研究流域面积较小,如果存在不闭合量,不闭合量占总径流量的比例就会比较大,从而对径流量及流量过程线产生较大影响.

1.2 次洪模拟

次洪模拟收集了1973年、1977年、1982年和1983年这4个年份的洪水资料,共选取了8场次洪水.其中前6场用于率定次洪模型参数,后2场用于检验次洪模型参数.次洪模型模拟计算的时段长取为1h.对于与时段长无关的参数,使用日模相应的值.与时段长有关的次模参数率定顺序为SM→CS→CI.在采用次洪模型模拟时,低水点据不多,为突出高水部分的作用,则以误差的绝对值为目标函数[10].计算公式为

式中:Si——第i场洪水流量过程线误差的绝对值;¯S——n场洪水流量过程线误差绝对值的平均值.

计算结果见表3和表4.

表3 率定场次次洪模拟结果Table 3 Simulation results of floods in calibration years

表4 检验场次次洪模拟结果Table 4 Simulation results of floods in examining years

从表3和表4可以看出:(a)洪水过程上涨段陡峭,退水段则上部陡降,下部退水明显变缓,且多处转折,持续时间较长;(b)实际流域下垫面对洪水产汇流过程有坦化作用;(c)洪水过程常呈现出具有较大底水流量的复峰;(d)检验的2场洪水代表性不够,洪量都偏小,洪水过程易受外部条件的影响.

2 模型的改进

为了使新安江模型能更适用于具有不均匀下垫面的岩溶地区,根据岩溶地区独特的水文地质特性以及此次模拟结果,对新安江模型在岩溶地区的应用提出了一些改进的设想:(a)由于岩溶流域内覆盖土层一般较薄[11],植被差,流域实际蒸散发量和缺水容量均小于非岩溶地区,可以忽略由于深根植物散发引起的土壤深层蒸散发,而采用2层蒸散发模型进行计算.(b)我国南方大部分岩溶流域气候湿润,土层较薄,下渗能力强,包气带缺水量不大,易为一般的雨量所满足,即达到田间持水量要求,所以在岩溶地区采用蓄满产流方式计算产流量基本符合实际情况.为了使后面分水源及汇流阶段模拟得更加准确,可以将岩溶流域下垫面透水面积划分为非岩溶区和岩溶区,其中岩溶区又分为裸露岩溶区和土壤覆盖岩溶区2类.(c)由于补给强度、径流成分和汇流速度等有所不同,被调蓄程度和时程分布不一,将径流划分为地表径流、壤中流、快速地下径流和慢速地下径流,并分别采用不同的方法进行计算[12].地表径流采用无因次单位线或滞洪演算法,壤中流、快速地下径流和慢速地下径流则分别采用不同的线性水库进行汇流计算,最后线性叠加得到流域出口断面总出流[13].

根据第1种设想,尝试把新安江日模型的3层蒸散发结构改为2层蒸散发结构.对比分析改进前后的模拟结果可知,除1974年确定性系数稍有减小外,其余10个年份的确定性系数各有不同程度的提高.由此可以证明,改进后的模型模拟精度较改进前有所提高,所以可以岩溶地区为例对改进后的新安江模型进行进一步的研究和检验.表5和表6为改进前后的计算结果对比.

表5 率定年份改进前后日模模拟结果对比Table5 Comparison of daily simulation results of original model and improved model in calibration years

表6 检验年份改进前后日模模拟结果对比Table6 Comparison of daily simulation results of original model and improved model in examining years

3 结 语

岩溶地区的实测水文资料相对贫乏,在岩溶流域建立完整精确的流域水文模型存在一定的困难.在目前尚未有较适用模型的情况下,笔者选用新安江模型并根据具体情况对其进行了适当的改进.实例应用结果表明,将新安江模型的3层蒸散发结构改为2层蒸散发结构,不仅能较大地提高该模型在岩溶地区的适用性,而且方法简便并易于实施.

[1]赵人俊.流域水文模拟[M].北京:水利水电出版社,1984.

[2]李致家,姚成,汪中华.基于栅格的新安江模型的构建和应用[J].河海大学学报:自然科学版,2007,35(2):131-134.(LIZhijia,YAOCheng,WANG Zhong-hua.Development and application of grid-based Xin'anjiang model[J].Journal of Hohai University:Natural Sciences,2007,35(2):131-134(in Chinese))

[3]胡松,梁虹,刘善霞.喀斯特流域洪水研究:以贵州省为例[J].水科学与工程技术,2009(1):36-38.(HU Song,LIANG Hong,LIU Shan-xia.Study on the flood in Karst Drainage Basins:a case study in Guizhou Province[J].Water Sciences and Engineering Technology,2009(1):36-38.(in Chinese))

[4]杨明德.岩溶流域水文地貌系统[M].北京:地质出版社,2002.

[5]郝庆庆,陈喜,马建良.南方喀斯特流域枯季退水影响因子分析[J].水土保持研究,2009,16(6):74-77.(HAO Qing-qing,CHENXi,MA Jian-liang.Analysis on low-flow recession influencing factors in South Karst Basin[J].Research of Soil and Water Conservation,2009,16(6):74-77.(in Chinese))

[6]郝庆庆,陈喜,马建良.新安江模型在贵州岩溶地区的改进与应用[J].水电能源科学,2009,27(4):52-54.(HAO Qing-qing,CHENXi,MA Jian-liang.Improvement and application of Xin'anjiang model in Guizhou Karst area[J].Water Resources and Power,2009,27(4):52-54.(in Chinese))

[7]李致家,周轶,哈布◦哈其.新安江模型参数全局优化研究[J].河海大学学报:自然科学版,2004,32(4):376-379.(LIZhi-jia,ZHOUYi,HAPUARACHCHI H A P.Application of global optimization to calibration of Xin'anjiang model[J].Journal of Hohai University:Natural Sciences,2004,32(4):376-379.(in Chinese))

[8]王佩兰,赵人俊.新安江模型(三水源)参数的客观优选方法[J].河海大学学报,1989,17(4):65-69.(WANG Pei-lan,ZHAO Ren-jun.Optimazation method of calibration of Xin'anjiang model(3 components)[J].Journal of Hohai University,1989,17(4):65-69.(in Chinese))

[9]瞿思敏,包为民,张明,等.新安江模型与垂向混合产流模型的比较[J].河海大学学报:自然科学版,2003,31(4):374-377.(QU Si-min,BAO Wei-min,ZHANG Ming,et al.Comparison of Xin'anjiang model with vertically-mixed runoff model[J].Journal of Hohai University:Natural Sciences,2003,31(4):374-377.(in Chinese))

[10]CARTER J M,DRISCOLL D G.Estimating recharge using relations between precipitation and yieldin a mountainous area with large variability in precipitation[J].Journal of Hydrology,2006,316:71-83.

[11]LONG A J.Hydrograph separation for karst watersheds using a two-domain rainfall-dischargemodel[J].Journal of Hydrology 2009,364:249-256.

[12]DAVISA D,LONGA J,WIREMANM.KARSTIC:a sensitivity method for carbonateaquifers in Karst terrain[J].Environmental Geology 2002,42:65-72.

[13]LONG A J,PUTNAML D.Age-distribution estimationfor karstgroundwater:issues of parameterizationand complexity in inversemodeling by convolution[J].Journal of Hydrology,2009,376:579-588.