Timoshenko梁的动力问题探讨——基于回转射线矩阵法的动力响应分析

李凤臣， 郑喜亮， 张丽娜

(1.东华理工大学建筑工程学院，江西 抚州 344000;2.中冶赛迪工程技术股份有限公司，重庆 400013)

近年来，大型土工结构的动力学问题研究越来越受到工程界的广泛关注，特别是建筑结构物在动力荷载(地震、风、冲击荷载等)作用下的响应问题更是不容忽视。虽然结构动力响应的计算方法很多，在实际工程中的应用也很广泛，但结构波动和振动特性的基础研究进展却很缓慢(钱七虎，2004;孙占学等，2004)。

求解任意动力荷载作用下结构的动力响应所采用的方法大多是直接积分法，钟万勰(1995)、彭建设等(1998)、于开平(2004)对此类方法进行深入的研究和探讨。但这种方法只能求出近似解，不能求出精确解，且它的计算精度与时间步长有很大关系，有比较突出的精确性、收敛性和稳定性的问题(喻晓今，2004;杨恒山，2008)。

求解结构动力响应的精确解法主要有模态叠加法(MSM)、传递矩阵法(MTM)和回转射线矩阵法(MRRM)。模态叠加法是比较早的计算结构动力响应的方法，最初主要是用在计算多自由度离散体系动力学方面，在克拉夫(2006)的著作中有详细的论述，对于分布体系，用模态叠加法求解动力响应较为困难。林继德(1992)对结构动力计算中振型叠加法作了进一步研究，修正了模态叠加法中计算无质量处的位移算法。传递矩阵法最早由Thomson(1950)提出，用于求解非均匀梁振动问题的矩阵方法，此外还应用在分析声波在多层介质中的传播问题(Adler，1990;Lowe，1995)。芮筱亭等(1995)将传递矩阵法应用到多体系统的振动问题中，提出了计算多体系统振动响应的新方法;朱勇涛等(2002)提出了变截面梁弯剪振动的传递矩阵法求解方法。模态叠加法是将自振频率的模态按照傅立叶积分定理组合而成，但由于自振频率不完整，使得结果误差较大，而传递矩阵法的矩阵中含有超越函数，又有累积误差。

针对模态叠加法和传递矩阵法求解结构动力响应精度方面的不足，Howard等(1998)和Pao等(1999，2003)提出了一种全新的计算方法，即回传射线矩阵法，应用该方法计算桁架中应力波的传播，并通过试验证明了计算的准确性;之后又将该方法应用在框架动力响应中和平面桁架动力响应计算中，均得到了很好的结果。郑喜亮(2007)研究表明，回传射线矩阵法在计算结构自振频率及动力响应时，不仅可以得到比传递矩阵法更好的结果，而且还能计算结构的瞬态响应，这是传递矩阵法很难做到的。

1 回传射线矩阵法的基本原理

1.1 散射矩阵S

首先引入双坐标系统:局部坐标系统和整体坐标系统，如图1所示。对杆IJ，一个局部坐标系统为x－IJ，以I点为原点，x轴的正方向为正方向;另外一个局部坐标系统为x－JI，以J点为原点，x轴的负方向为正方向。

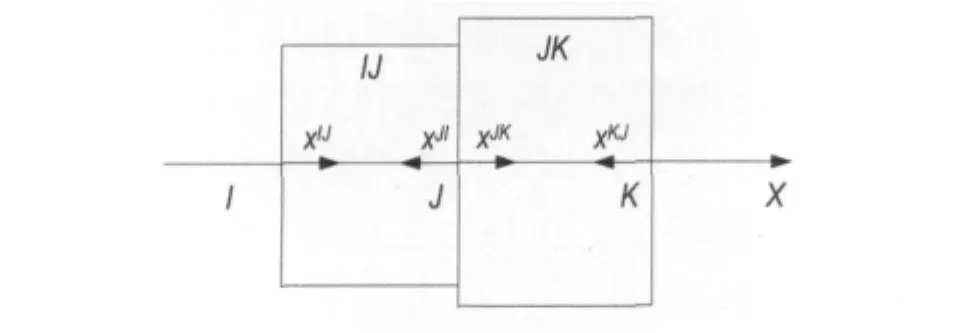
图1 双坐标系统Fig.1 Double coordinates system

能够得到杆系统的散射关系方程如下

其中

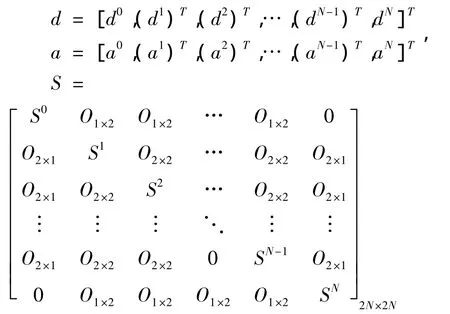
矢量d是整体离开波的向量，代表从各个节点离开的波;矢量a则是整体到达波的向量，代表到达各个节点的波。2N×2N的矩阵S是整体散射矩阵。

1.2 相位矩阵P和回传矩阵R

一段杆内的同一个波，既是左端点的离开波，同时也是右端点的到达波。两者的振幅相同，但相位不同，所以有如下相位关系

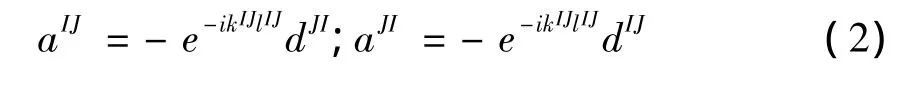
在J点处再引入一个新的局部矢量⇀dJ和一个新的整体离开波矢量⇀d，整体矢量⇀d和d的关系为

其中

故可将矢量a和⇀d关系写成

其中叫做整体相位变换矩阵。

联立方程(1)、(3)、(4)，得

此处R(ω)=SPU，称为回传矩阵。

2 应用传递矩阵法计算Timoshenko梁的动力响应

下面就只以单跨梁为例，介绍传递矩阵法求解结构稳态响应的过程。首先引入状态矢量的概念，对于Timoshenko梁上任意点i，其状态矢量可以表示为

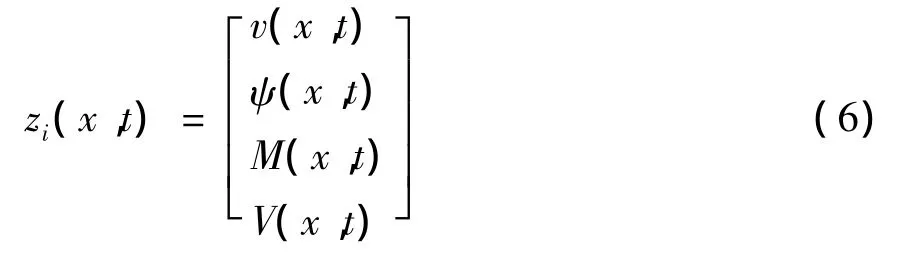
传递矩阵法就是建立节点与节点之间状态矢量的场传递矩阵和节点上左右两端之间状态矢量的点传递矩阵，然后将场矩阵和点矩阵组合起来，形成整体传递矩阵，最后根据边界条件，求解出梁的自振频率及相应的动力响应。

如图2所示的两端铰支的单跨Timoshenko梁，跨中施加集中简谐荷载

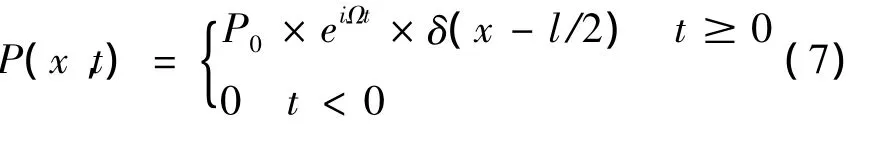
图2 简谐集中荷载作用的单跨梁Fig.2 Single-span beam under harmonic concentrated load

梁的振动频率与外界荷载相同，为Ω。所以在IJ段梁上，左端I节点的状态矢量为zI(0，Ω)，右端J节点的状态矢量为zJ(l/2，Ω)。两节点的状态矢量可以写成:zRI=zI(0，Ω)=MIR，zLJ=zJ(l/2，Ω)=MJR。

其中

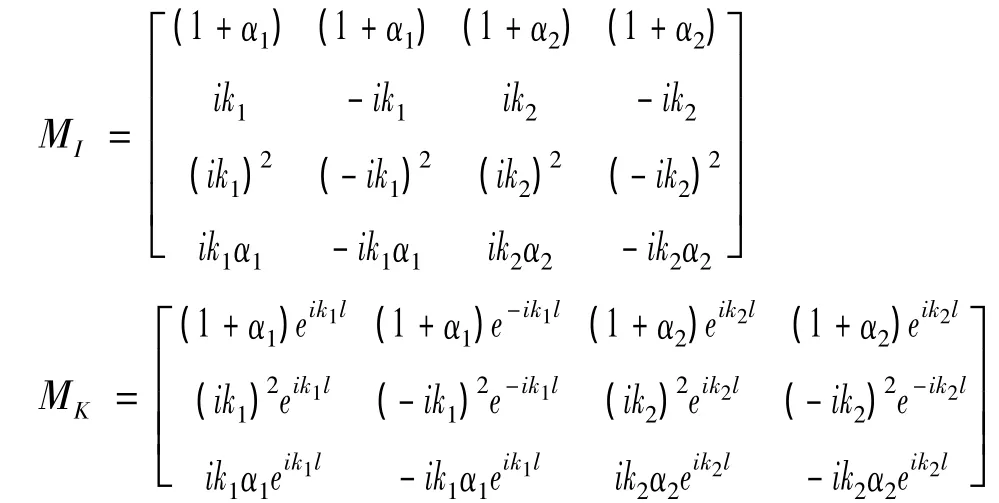
3 应用回传射线矩阵法计算Timoshenko梁的稳态响应

3.1 单跨Timoshenko梁的稳态响应

Timoshenko梁在频域的位移解为

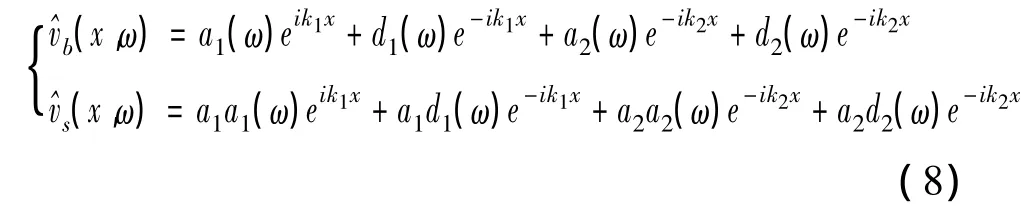
Timoshenko梁在各点的转角、剪力、弯矩等响应的频域解为

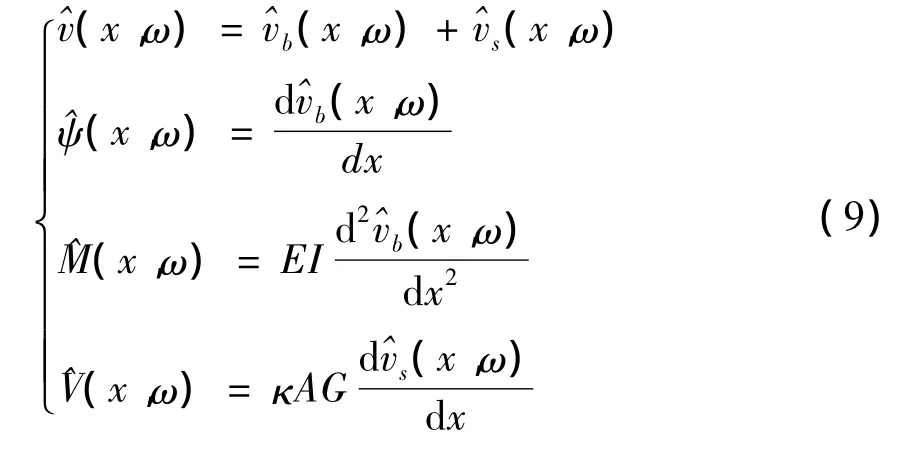
如图3所示的单跨两端固支的Timoshenko梁，跨中受集中简谐荷载P(x，t)作用，其表达式与式(7)相同。

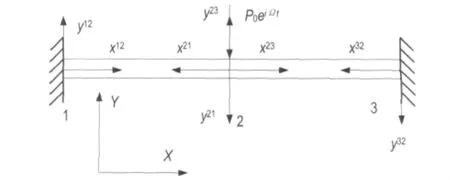
图3 两端固支单跨梁模型Fig.3 Single-span beam model with both ends fixed

整体的散射方程为:

求得参数a和d的值，在带入到式(8)中求得梁上各点位移响应的频域解，将参数a和d的值带入式(9)中，则可求出梁上各点的转角、剪力、弯矩等响应的频域解，将频域解进行傅立叶变换，则可得到梁响应的时域解。

3.2 两跨Timoshenko梁的稳态响应

如图4所示的两跨连续梁，两端为固定支撑，跨中为刚性支撑，其中一跨跨中作用简谐荷载。

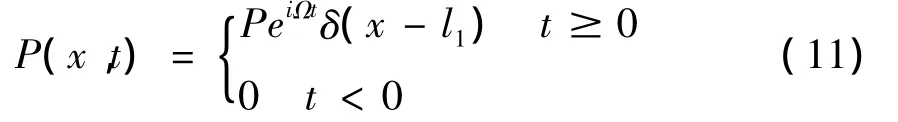
图4 两端固支双跨梁模型Fig.4 Two-span beam model with both ends fixed

系统的整体坐标为X-Y，将梁分成三个单元，四个节点:1-4，局部坐标如图4中所示。同样先推导系统的散射矩阵，求解响应的方法与单跨梁稳态响应的求解方法相同。

4 算例分析

4.1 单跨Timoshenko梁的稳态响应算例

如图3所示的两端固定的单跨低碳钢梁，其截面尺寸为:梁高 h=0.5 m，梁宽 b=0.04 m，梁长度L=2 m，密度 ρ=7 850 kg/m3，截面积 A=0.002 m2，弹性模量 E=206 GPa，剪切模量 G=79 GPa，剪切因子κ=0.833 3。这是一个比较典型的Timoshenko梁，表1给出了三种边界条件下，单跨梁上跨中施加简谐荷载，分别采用传递矩阵法(MTM)和回转射线矩阵法(MRRM)计算，各点稳态响应幅值的对比。其中，跨中施加荷载的大小为P0=1 000 N，荷载频率为Ω =100 rad/s，以梁长为长度基本单位进行无量刚计算，得到的各点的响应幅值均为无量纲结果。

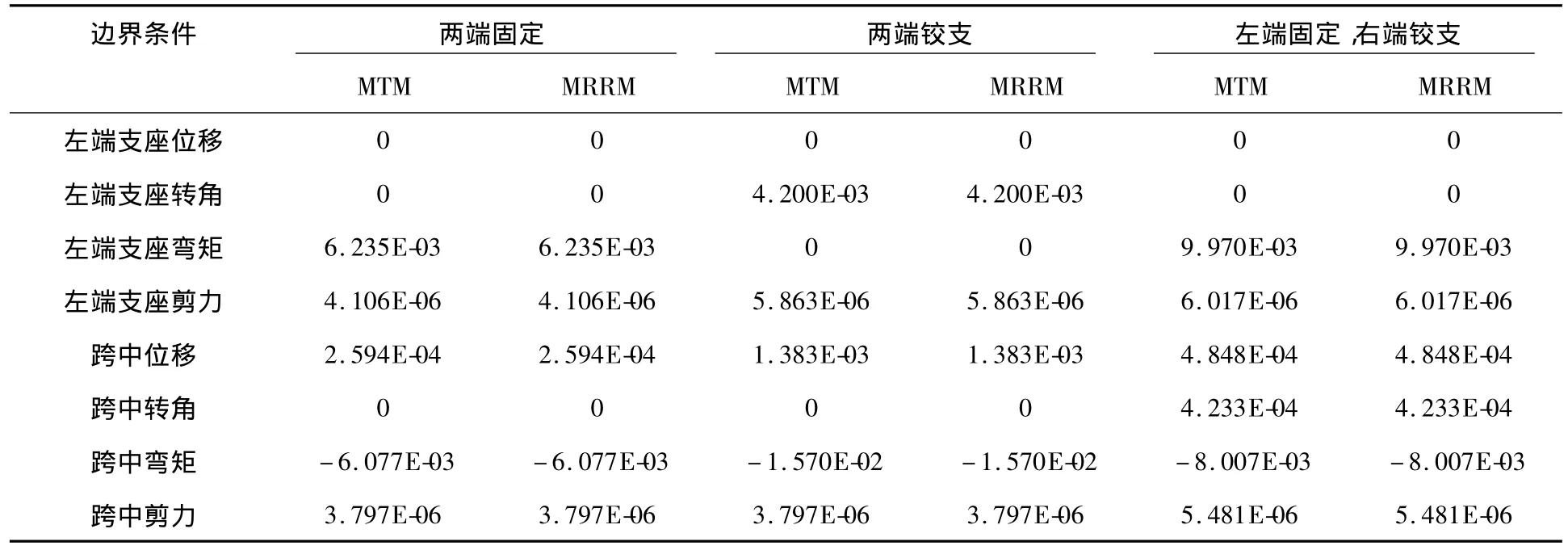
表1 MTM与MRRM计算单跨梁稳态响应各点响应幅值对比Tab.1 Comparison of the amplitude of steady-state response in each point of single-span beam computed with MTM and MRRM

4.2 两跨Timoshenko梁的稳态响应算例

表2给出了两跨连续梁在其中一跨跨中施加简谐荷载，分别采用传递矩阵法(MTM)和回转射线矩阵法(MRRM)计算，梁上各点稳态响应幅值的结果对比。其中，计算简图同图4，梁的截面尺寸同算。例4.1，两跨梁长均为1 m，左跨跨中施加荷载的大小为P=1 000 N，荷载频率为Ω=100 rad/s，以梁长为长度基本单位进行无量刚计算，得到的各点的响应幅值均为无量纲结果。

表2 MTM与MRRM计算两跨连续梁稳态响应各点响应幅值对比Tab.2 Comparison of the amplitude of steady-state response in each point of two-span continuous beam computed with MTMand MRRM

5 结论

传递矩阵法适用于计算单跨梁、多跨连续梁的自振频率、稳态响应，在计算自振频率时，前几阶的计算精度很高，但随后就会出现严重的数值稳定问题，而无法继续计算更高阶的频率。回传射线矩阵法适用于计算单跨梁、多跨连续梁的自振频率、稳态响应和瞬态响应。通过以上的对比，可以看出，回传射线矩阵法，有适用范围广、计算精确、算法简洁明了以及便于编程等特点。

林继德.1992.结构动力计算中振型叠加法的进一步研究[J].工程力学，9(3):131-135.

彭建设，张敬宇.1998.由Gurtin变分原理求解一维动力响应的半解析法[J].力学学报，26(6):708-711.

钱七虎.2004.深部岩体工程响应的特征科学现象及“深部”的界定[J].东华理工学院学报，27(1):1-5.

芮筱亭，陆毓琪.1995.多体系统振动的传递矩阵法[J].宇航学报，16(3):41-47.

孙占学，朱永刚，张文.2004.矿物-水反应的地球化学动力学研究进展[J].东华理工学院学报，27(1):14-18.

克拉夫R，彭津J，王光远译.2006.结构动力学[M].北京:高等教育出版社.

杨恒山.2008.向量加权平均值在桥梁控制网平差中的应用[J].东华理工大学学报:自然科学版，31(3):256-258.

于开平.2004.结构动力响应数值分析的新的广义-α方法的频率域分析[J].振动工程学报，17(4):393-398.

喻晓今.2004.求梁位移的比拟梁法[J].东华理工学院学报，27(4):398-400.

郑喜亮.2007.基于回传射线矩阵法的Timoshenko梁动力响应分析[D].杭州:浙江大学硕士论文.

钟万勰.1995.暂态历程的精细计算方法[J].计算结构力学及其应用，12(1):1-6.

朱勇涛，易传云.2002.变截面梁弯剪振动的传递矩阵法求解[J].机械传动，26(2):22-23.

Adler E L.1990.Matrix methods applied to acoustic waves in multilayers[J].IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，37(6):485-490.

Howard S M，Pao Y H.1998.Analysis and experiments on stress waves in planar trusses[J].Journal of Engineering Mechanics，124(8):884-891.

Lowe M J S.1995.Matrix techniques for modeling ultrasonic waves in multilayered media[J].IEEE on Ultrasonics，Ferroelectrics，and Frequency Control，42(4):525-542.

Pao Y H，Keh D C，Howard S M.1999.Dynamic response and wave propagation in plane trusses and frames[J].AIAA Journal，37(5):594-603.

Pao Y H，Sun G.2003.Dynamic bending strains in planar trusses with pinned of rigid joints[J].Journal of Engineering Mechanics，129(3):324-332.

Thomson W T.1950.Matrix solution for the vibration of uniform beams[J].Journal of Applied Mechanics，17:337-339.