两种群动力学模型的Matlab仿真
刘 波
(湖北民族学院理学院,湖北恩施445000)
对种群动力学模型而言,计算机数值仿真是模型检验和预测的一种重要手段[1-3].计算机数值仿真可以将抽象复杂的理论研究结果,转化成易于人们理解的数值序列或图形演示,使复杂的动力学分析和数量巨大的参数筛选及动态过程的模拟成为可能[4].基于Matlab的两种群动力学模型数值仿真手段主要有三种:时间序列图、斜率场图、相平面轨迹图[5-7],时间序列图能够直观反映种群随着时间演化的趋势,例如持续生存性、绝灭性和周期性.斜率场图和相平面轨迹图都属于相平面图形,尤其适合反映种群的相关变化趋势.斜率场图的最大优势在于从整体反映斜率场的分布,且不必求解微分方程.相平面轨迹图的最大优势在于对应不同初值条件反映轨线的走向,有助于分析系统的稳定性.综合运用以上三种数值仿真手段,可以进一步揭示两种群动力学模型更为复杂的渐近行为.
1 两种群动力学模型的Matlab仿真
考虑一类经典的Lotka-volterra两种群动力学模型:

r1和r2分别表示两种群的内禀增长率,a和d分别表示两种群的种内作用系数,b和c分别表示两种群的种间作用系数,为了揭示模型(1)的渐近行为,下面分别采用时间序列图、斜率场图、相平面轨迹图三种不同的仿真手段,编写Matlab程序对模型(1)进行数值仿真.根据实际生物意义,以下仅在区域R2+={(x,y)|x≥0,y≥0}中绘制图形.
1.1 时间序列图
在模型(1)中,取 r1=1,a=0,b=-0.1,r2=-0.5,c=0.02,d=0 得到如下系统:

对系统(2),只要给定初值条件(x0,y0),即可利用函数ode45求得数值解,由此绘制的图形x(t)和y(t)称为时间序列图.下面给出绘制系统(2)时间序列图的Matlab程序及图例:
function xdot=TimeSeries(t,x)
r1=1;a=0;b=-0.1;r2=-0.5;c=0.02;d=0;
xdot=[x(1)*(r1+a*x(1)+b*x(2));x(2)*(r2+c*x(1)+d*x(2))];
functionLoadTimeSeries(x0,y0)%LoadTimeSeries(25,2)
tspan=0:0.01:25;cond0=[x0,y0];
[t,x]=ode45('timeseries',tspan,cond0);
plot(t,x(:,1),'r-',t,x(:,2),'b-');legend('x(t)','y(t)');xlabel('t');ylabel('x(t)and y(t)');
通过观察图1所示时间序列图,可以分析得知系统(2)在初值条件cond0=[25,2]下,种群x和种群y持续生存,且呈现出近似周期性.
1.2 斜率场图
在系统(2)中,消去dt可以得到形如dy/dx的斜率表达式,在R2+中取定一矩形区域并称之为场,自场中每一点(xi,yi)引出斜率为Ki的短线段,由此绘制的图形就是斜率场图.下面给出绘制系统(2)斜率场图的Matlab程序及图例:
function SlopesField(r1,a,b,r2,c,d)%SlopesField(1,0,-0.1,-0.5,0.02,0)
syms x y;fun=y*(r2+c*x+d*y)/(x*(r1+a*x+b*y));hx=120/30;hy=30/30;x0=0;y0=0;hold on
for i=1:30,x=x0+(i-1)*hx;for j=1:30,y=y0+(j-1)*hy;k=eval(fun);
if abs(hx*k)>hy,plot([x,x+hy/k*2/3],[y,y+hy*2/3]);else plot([x,x+hx*2/3],[y,y+hx*k*2/3]);end;end;end;
xlabel('x');ylabel('y');box on;warning off;
通过观察图2所示斜率场图,可以分析得知系统(2)在不同初值条件下,斜率场围绕在正平衡点(25,10)周围,种群x和种群y持续生存,从场中一点出发即可判断出大致走向.
1.3 相平面轨迹图
在系统(2)中,考虑将数值解法求得的时间序列数据x(t)和y(t)绘制在相平面XOY上,由此得到的图形称为相平面轨迹图.下面给出绘制系统(2)相平面轨迹图的Matlab程序及图例:

通过观察图3所示相平面轨迹图,可以分析得知系统(2)在不同初值条件,轨线以正平衡点(25,10)为中心环状分布,种群x和种群y持续生存,进一步验证可知系统是全局一致渐近稳定的[7].

图1 时间序列图Fig.1 Time series plot

图2 斜率场图Fig 2 Field of slopes
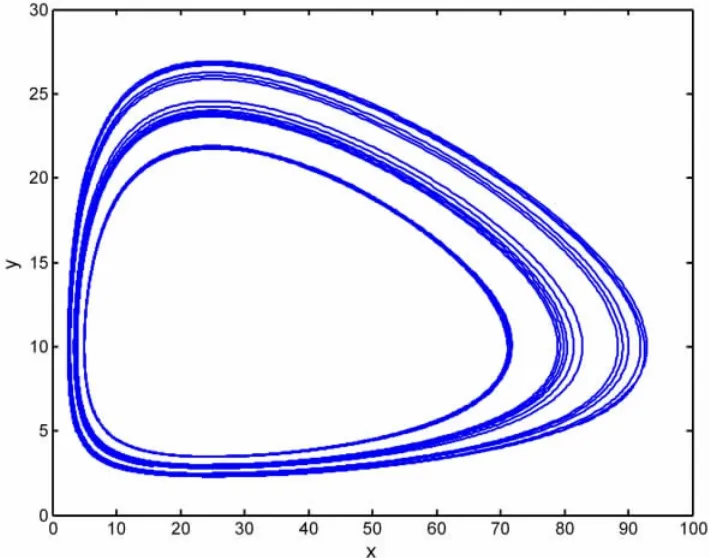
图3 相平面轨迹图Fig 3 Phase plane plot
2 总结和讨论
本文分析和对比了三种不同的数值仿真手段在两种群动力学模型仿真中的应用,通过编写Matlab程序对一类经典的Lotka-volterra两种群动力学模型进行数值仿真,结果表明目前使用较为广泛的时间序列图在确定周期性上并不准确,斜率场图最值得关注的特点是不必求解微分方程,相平面轨迹图则弥补了斜率场图在方向性上的不足,并且对系统稳定性分析有直接帮助.综合应用本文介绍的三种数值仿真手段,可以帮助我们更加深刻地认识和理解种群动力学模型背后复杂的渐近行为.
[1] 刘波.单种群动力学模型的MATLAB仿真[J].湖北民族学院学报:自然科学版,2011,29(4):368-370.
[2] 梁仁君,林振山,韩洪凌,等.物种对资源竞争的动力机制及数值模拟[J].生态学报,2007,27(12):5390-5397.
[3] 刘波,刘志军.一类食饵具有S-型变收获率的非自治离散捕食系统渐近行为[J].生物数学学报,2012,27(3):499-506.
[4] 黄樨.数学与计算机仿真在生态学研究中的应用[J].南京林业大学学报,2009,25(5):63-66.
[5] 桂占吉.生物动力学模型与计算机仿真[M].北京:科学出版社,2005.
[6] 马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.
[7] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

