G2连续的圆弧样条曲线插值
齐 倩,方美娥
(杭州电子科技大学计算机学院,浙江杭州310018)
0 引言
用圆弧作为样条来进行造型而得到的样条曲线称为圆弧样条曲线,简称圆弧样条。人们在对圆弧样条的研究中取得了很多成果,不仅介绍了圆弧样条,还用分析方法讨论了圆弧样条插值方法[1,2],并提出了圆弧样条插值问题[3]和双圆弧样条[4]。在圆弧样条的插值问题中,以前大多采用的是逼近算法,后来在不断的研究中,又取得了很多新的研究成果,找到了一条由直线和圆弧构成的G0圆弧样条曲线[5]和用最小二乘法来构造由圆弧和直线段构成的G0或G1曲线的方法[6],通过解一个非线性方程组来求得拟合给定型值点的圆弧样条[7]和采用一些简单的公式和比较简单的方法来求得G1圆弧样条曲线[8],还有的给出了一种用二次曲线段来插值平面有序数据点列[9]和所构造的三圆弧样条曲线可以在插值点处按切向和曲率插值的方法[10]。文献11提出替换平面圆弧样条曲线的一部分,以增加平面圆弧样条曲线的光滑度,进而产生G2连续的曲线。本文在已有研究工作的基础上,提出了一种G2连续且保凸的圆弧样条的算法。突破了圆弧段首末端点固定为插值点的限制条件,插值出了整体G2连续的圆弧样条曲线,而且构造出的差值曲线是唯一可实现整体细分生成的圆弧样条曲线。
1 G2圆弧样条插值曲线的构造
在平面上给定由n个点P1,P2,…,Pn所组成的点列,及其每一端点处的切向 T1,T2,…,Tn,求一条由若干段圆弧构成的G2连续的曲线,使它依次插值于点列,且在每一端点处的切向为T1,T2,…,Tn,要得到满足条件的圆弧样条曲线。
1.1 初始圆的构造
为每个型值点构造唯一的初始圆需首先确定初始圆的半径及圆心位置,为实现插值曲线G2连续,本文构造相同半径的初始圆。半径的选取可作为自由参数由用户确定,但必须保证后续公切圆的存在。令过两个相邻的型值点P1、P2作半径为r的圆C1、C2,使得两圆的半径同样为R的公切圆圆心与O1、O23点共线,根据三角形的性质得:
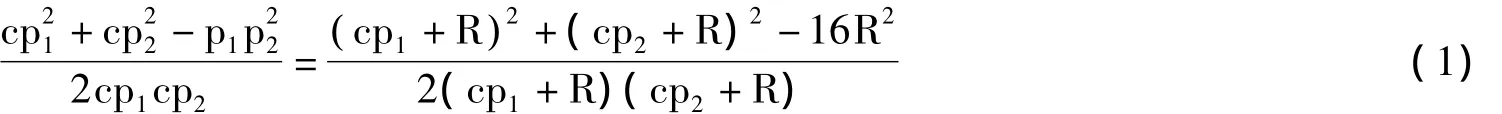
如图1所示,每相邻两型值点对应的R可以从式1中求出,令所有R中的最小值为Rmin,则只需选择初始圆半径r>Rmin即可保证G2连续圆弧样条存在,且一般选取半径不超过dmax为相邻插值点距离最大值)较为合适,尽量避免相邻圆的包含。
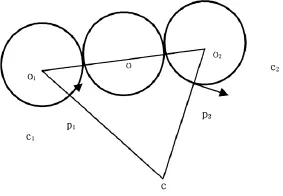
图1 初始圆半径确定方法图
对于一个型值点,已知切向和初始圆的半径,可以作2个圆,在这里选取外侧的圆作为初始圆。具体方法如下:构造一个坐标系,坐标原点平移到插值点,坐标轴旋转到以切矢为x轴正向的位置,此时圆心落在纵坐标大于O的区域内的插值圆符合要求,即处于曲线外侧。
1.2 公切圆的作法

实际上,按上述方法确定的公切圆有2个,按照选取初始圆的类似方法确定坐标系后选取圆心纵坐标小于O的公切圆,这样选取的公切圆处于最终得到的插值曲线的内侧,可更好地保证插值曲线简单光顺。
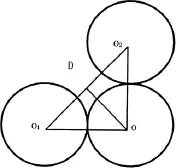
图2 公切圆圆心选取方法图示
1.3 圆弧段的选定
初始圆与公切圆确定之后,从第一个型值点出发沿切向在初始圆和公切圆上选取合适的圆弧段,形成一条连续的圆弧样条曲线。圆弧段的选择标准满足两条原则,一是让选取的圆弧段依次经过各个型值点,二是尽量选取较短的圆弧段。一般情况都能选取较短的圆弧段,插值点越均匀,效果越好,极不均匀时有可能取整圆并重复一段圆弧,但G2的路径总是存在的。
从以上算法可知,本文方法构造出的插值曲线上所有点的曲率均为1/r,因此整条圆弧样条插值曲线自然满足G2连续。如图3所示,粗线为最终的圆弧样条曲线,其中图3中4个插值点取自同一半径为r的圆上,可以看到利用本文的方法选取初始圆半径为r时,所有公切圆均为型值点所在的圆,此时插值曲线具有保圆性。
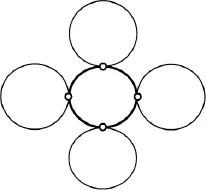
图3 本文方法举例
2 G2圆弧样条曲线细分
由文献12中第5节中圆弧段细分公式可知,细分参数仅与圆弧段的半径及弧度相关,本文生成的圆弧样条插值曲线是由半径相同的圆弧段连接而成,如果进一步将这些圆弧段重新均分为同弧度的圆弧段,则可由文献12中的细分方法整体细分生成,本文方法得到的圆弧样条插值曲线如图4(a)所示,凹圆弧是初始圆上选取的圆弧段,凸圆弧是公切圆上选取的圆弧段,半径相同,弧度分别为 和,为了统一弧度,将这两类圆弧段分别划分为弧度为3段及2段圆弧,这样划分后的每一段新圆弧段细分生成的控制多边形为两条边的折线,两条边分别以圆弧段的首末端点为中点且与之相切,这样整条圆弧样条曲线的细分控制多边形由这些折线连接而成,如图4(b)所示,圆点为相应控制顶点,由此确定了控制多边形、半径及弧度的圆弧样条可由文献12中的方法整体细分生成,细分曲线如图4(b)所示,与原来的圆弧样条插值曲线重合。这是本文方法与已有圆弧样条插值方法相比,除具有更高几何连续阶之外的又一突出优势,首次实现了圆弧样条曲线的整体细分生成,可为数控加工中刀轨路径设计等应用带来很大的方便。
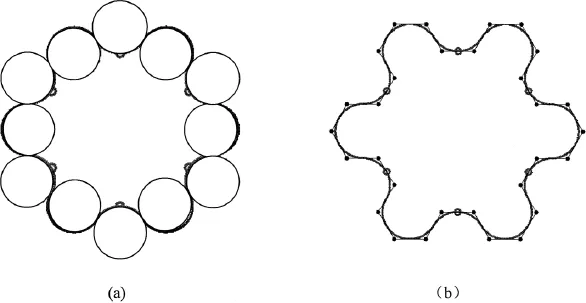
图4 细分实例
3 结束语
根据以前的研究,构造既插值型值点又插值切向的圆弧样条曲线只能达到切向连续,本文提出了一种新的简单的圆弧样条构造方法,使得到的圆弧样条曲线满足曲率连续。该方法具有如下特点:圆弧段之间的连接点不一定是在给定的插值型值点上,因此,有更多的自由度来控制曲线形状;圆弧样条曲线的圆弧段数不大于型值点数;生成的圆弧样条曲线具有保凸性;且此种算法不仅适用于开圆弧样条,对闭圆弧样条也同样适用;最终的插值圆弧样条可以整体细分生成。但该方法也有拐点较多的不足,实际中可以少取一些型值点,或尽量取型值点为所构造的圆弧段的中点来加以改善。
[1]孙家昶.局部坐标下的样条函数与圆弧样条曲线[J].数学学报,1977,20(4):28-40.
[2]孙家昶.样条函数与计算几何[M].北京:科学出版社,1982:271-291.
[3]苏步青,刘鼎元.计算几何[M].上海:上海科学技术出版社,1981:176-213.
[4]董光昌,梁友栋,何援军.样条曲线拟合和双圆弧逼近[J].应用数学学报,1978,1(4):330-340.
[5]Piegl L.Curve fitting algorithm for rough cutting[J].Computer Aided Design1986,18(2):79 -82.
[6]Albano A.Representation of digitized contours in terms of conic arcs and straight-line segments[J].Computer Graphics&Image Processing,1974,3(1):23 -33.
[7]Hoschek J.Circular splines[J].Computer Aided Design,1992,24(11):611 -618.
[8]Meek D S,Walton D J.Approximation of quadratic Bezier curves by arc splines[J].Journal of Computational and Applied Mathematics,1994,54(4):107 -120.
[9]张三元.一种G2连续的二次曲线样条插值方法[J].计算机辅助设计与图形学报,2000,12(6):419-422.
[10]林杰,潘日晶.数据点列的三圆弧样条插值[J].福建师范大学学报,2007,23(2):20-24.
[11]Li Z,Meek D S,Smoothing an arc spline[J].Computer& Graphics,2005,29(4):576 -587.
[12]Fang M,Ma W,Wang G.A generalized curve subdivision scheme of arbitrary order with a tension parameter[J].Computer Aided Geometric Design,2010,27(9):720 -733.

