弹簧振子经验公式拟合的可信赖度分析
彭厚德
(长江师范学院物理学与电子工程学院,重庆 涪陵 408100)
在对弹簧振子的研究中,人们的研究主要集中在:1)弹簧质量对振动系统的影响问题[1-2];2)从不同角度定量分析弹簧质量对振动系统的周期和振幅的影响[3];3)质量、摩擦阻力等因数对弹簧振子系统运动性质的影响[4];4)弹簧等效质量对弹簧振子的运动状况的影响[5-8].在实验中获得弹簧振子运动方程所采取的方法大都是利用最小二乘法拟合得到.
最小二乘法对经验公式有着重要的作用[9].从各种文献来看,很少涉及到对最小二乘法所得结果的可信赖度分析,而是停留在对结果的简单误差分析,或与理论公式对照来确定经验公式拟合的好坏.对于利用最小二乘法获得的弹簧振子的经验公式进行可信赖度分析,可以清楚地判断结果的正确性以及可信赖程度.本文阐明对弹簧振子经验公式拟合的可信赖度分析方法.
1 回归分析原理
回归分析被广泛用于寻求两个或多个变量之间的内在关系,以求获得比较符合事物内部规律的最佳数学表达式.回归分析应解决变量之间的数学关系(回归方程)的获得、回归方程的可信赖度的统计检验以及因素分析等问题[10-13].
1.1 回归方程的获得
设因变量y与另外M个自变量xi的某种内在联系是线性的,通过实验得到N组数据xti(t=1,2,…,N),且其关系为

根据最小二乘法原理,b0,b1,…,bM应使得全部观察值yt与回归值^y的残差平方和为最小:
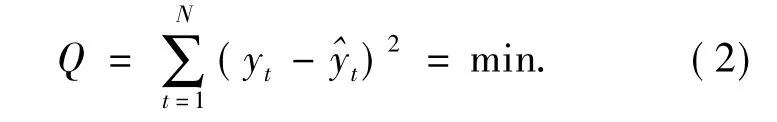
1.2 回归分析可信赖度的统计检验
获得回归方程后,并不一定能说明该回归方程正确表明了各变量之间的内在关系.这必须通过对该回归方程的统计检验才能说明其正确性.
对于回归方程的统计检验,首先应将各观测值 yt(t=1,2,3,…,N) 差异分为两部分,即由自变量x取值的不同与除此之外的其他因素的影响.由于此差异来自于各观测值与观测值的算术平均值之差,称为总变差:

将(3)式展开,同时考虑到交叉项为零,则有:

其中,U称为回归平方和,反映了在y的总变差中由于x和y的线性关系引起y的变化部分,其自由度为1;Q称为残余平方和,反映了除x和y的线性关系之外的一切因素对y的变差的作用,其自由度为N-1,且
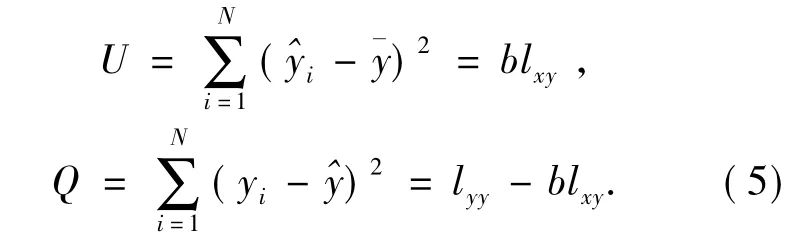
判断回归方程是否显著,取决于U和Q的大小比较,如果前者大大地大于后者,说明所得到的方程中各个变量之间的内在联系已经被准确地反映出来,而其他干扰因素的影响很小,结果可信赖度很高.这个比较可利用F检验来完成.根据F检验规则有:

在给定显著水平时,根据U和Q的自由度由F分布表查出Fα,将其与(6)式计算结果比较.若F>Fα,则认为在该显著水平α上回归显著,即因变量与自变量之间的关系应该是线性的,且非线性的其他因素影响很小.
对于多元线性回归分析,可按照表1所示方法计算.
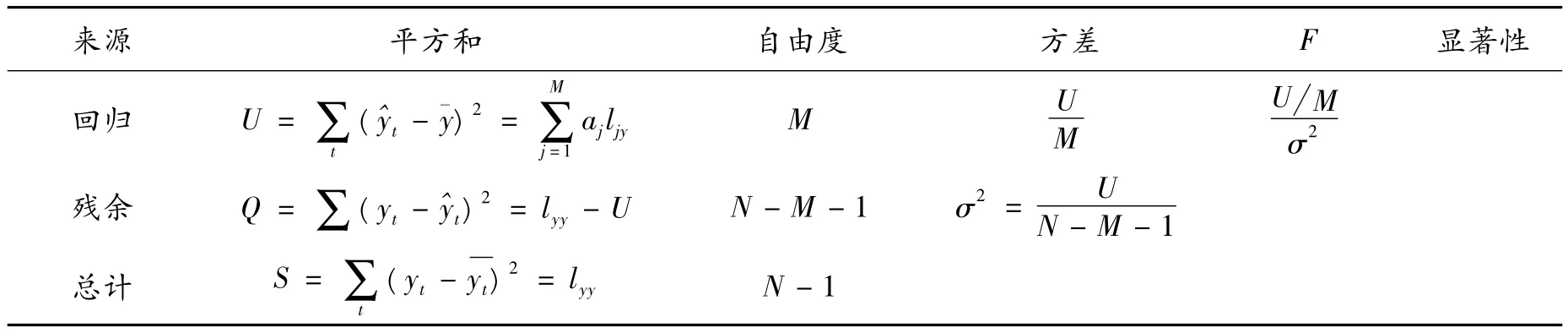
表1 多元线性回归分析计算方法
回归方程显著性的检验可使用残余平方和对回归平方和的F检验进行,表1中F为F检验的数学统计量:

和一元回归一样,当F≥Fa(M,N-M-1)时,认为回归方程在a水平上显著.
多元回归方程的预报精度由残余标准差给定:

2 弹簧振子经验公式的获得及可信赖度分析
利用焦利氏秤测量弹簧振子的相关参数.实验中,取4种不同的弹簧组成4个弹簧振子,对其振动周期、质量进行测量,测量数据如表2~表5所示.

表2 弹簧振子质量测量数据

表3 弹簧振子劲度系数

表4 弹簧振子周期

表5 弹簧振子质量
2.1 弹簧振子经验公式的获得
由力学可知,弹簧振子的周期T与下列因素有关:1)弹簧的劲度系数k;2)弹簧振子的质量m.可假设弹簧振子的函数关系式为

上式中,A、α、β为3个待定系数.这是一个非线性关系.为了方便进行最小二乘法处理,对(9)式做线性化处理得

令

则(10)式可写成
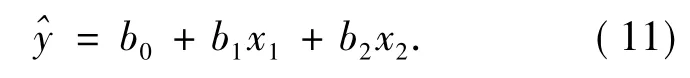
根据多元线性回归的最小二乘法原理,计算结果如表6所示.

表6 回归计算
按照多元回归分析法可得回归方程为
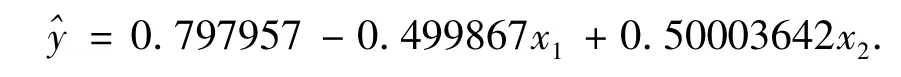
因为 b0=lgA,b1= α,b2= β,故 A,α,β 的值为

则弹簧振子的周期公式为

2.2 显著性和精度分析
根据上述数据和计算结果,根据表1,显著度分析计算结果如表7所示.

表7 计算数据
由于 F=92.39 > F0.01(2,9)=8.02 ,因此回归方程是0.01水平上显著.由(8)式可得,标准差为

F检验表明:在0.01显著水平上,回归平方和远大于残余平方和,回归高度显著;而除弹簧振子各变量之间的关系以外的其他因素的影响可以忽略不计.这意味着(12)式中给出的弹簧振子各变量之间的关系是准确的.
3 结论
综上所述,可以得到如下结论:
1)对弹簧振子公式的实验拟合,虽然实验方案并不复杂,实验器材要求不高,但获得的结果精度却非常高,并且利用科学的方法进行了检验,充分证明了所得表达式的正确性.这说明,可以利用简单的实验得到物理规律.但是,对得到结果只有经过科学、客观的检验后才能表明其正确性.
2)对弹簧振子经验公式的获得与可信赖度检验,可得到可信赖度分析的一般方法:
A.分析影响变量的主要因素;
B.利用最小二乘法获得经验公式;
C.分解总变差,得到回归平方和与参差平方和;
D.构建F变量,做F检验;
E.根据F检验判断经验公式的正确性与可信赖度.
[1]苏启录,陈金恩.弹簧振子问题探讨[J].福州师专学报,1999(6):26-28.
[2]程光明,石代蓉,陈希明.线性对称三弹簧振子振动的数值研究[J].重庆文理学院学报:自然科学版,2012,31(2):40-44.
[3]张忠厚.实际弹簧振子的振动问题[J].辽宁工程技术大学学报,2010(29):173-175.
[4]谢利民.弹簧振子运动的实际动力学分析[J].上海师范大学学报,2002(2):91-95.
[5]陈希明,潘娜娜,潘宇.无阻力任意摆角下配重复摆振动的数值研究[J].重庆文理学院学报:自然科学版,2012,31(1):45-49.
[6]詹士昌,徐婕.关于弹簧振子实验中实验条件的讨论[J].杭州师范学院学报,2006(2):114-117.
[7]鄢玉霞,吕建伟,宦强,等.弹簧振子实验方法的运用和改进[J].物理实验,2006(6):36-38.
[8]何晓明.利用数据处理总结经验公式[J].青海师范大学学报,2008(2):32-36.
[9]余长青.浅谈最小二乘法及其在科学实验中的应用[J].黔南民族师范学院学报,2005(6):53-56.
[10]邹乐强.最小二乘法原理及其简单应用[J].科技信息,2010(23):282-283.
[11]党兴菊,吴文良.最小二乘法拟合直线公式的初等推导[J].重庆科技学院学报,2010(4):185-187.
[12]王晓光,玉萍,王菊.最小二乘估值的计算方法[J].吉林建筑工程学院学报,2004(3):51-54.
[13]费业泰.误差理论与数据处理[M].合肥:机械工业出版社,2010:94-155.

