一类特殊本原有向图的广义的scrambling指数

孙琳莉，雷英杰

(中北大学数学系，山西 太原 030051)

如果存在正整数k，使得对于D中任意顶点u，v在D中都存在一点ω，都有从u到ω，从v到ω都有长为k的路径，则称满足上述条件的最小的正整数k称为D的scrambling指数，记为k(D)．对于任意的u，v∈V(D)，u，v的 scrambling 指数为

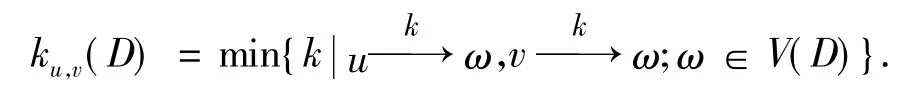
显然有：

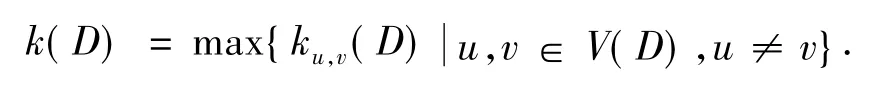
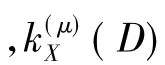
成立，则：

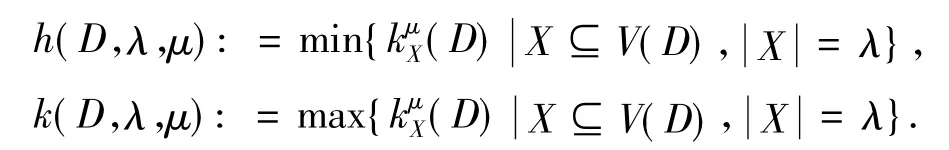
分别称为D的第λ重下μ-scrambling指数和第λ重上μ-srambling指数．

为方便起见，我们令

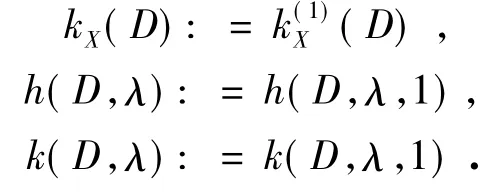
引理2［2］设D为含有一个Hamilton圈的n阶本原有向图，D中最小圈长为s，且1≤s≤n-1 ，如果 gcd(n，s)=1 ，则有：

k(D) ≤ K(n，s)=n-s+k(n，s) ．

其中

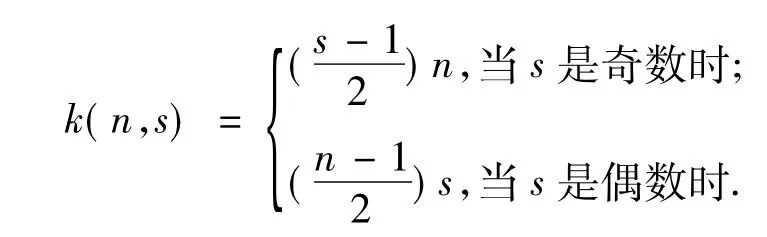
定理 3［2］设 D=Ds，n，gcd(n，s)=1 ，2≤ s≤ n-1，则有k(D)=K(n，s)．

1 主要结论

引理4 已知D是如图1所示的本原有向图，

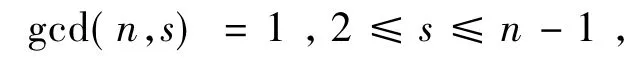
则有

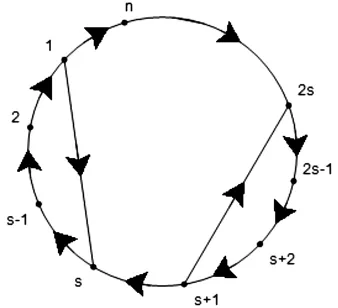
图1 本原有向图D

［1］Huang Yufei，Liu Bolian．Generalized scrambling indices of a primitive digraph［J］．Linear Algebra Applications，2010(433)：1798-1808．

［2］Akelbek M，Kirkland S．Coefficients of ergodicity and the scrambling index［J］．Linear Algebra Applications，2009(430) ：1111-1130．

［3］Chen Shexi，Liu Bolian．The scrambling index of symmetric primitive matrices［J］．Linear Algebra Applications，2010(433)：1110-1126．

［4］Akelbek M，Kirkland S．Primitive digraphs with the largest scrambling index［J］．Linear Algebra Applications，2009(430)：1099-1110．

［5］Liu Bolian，Huang Yufei．The scrambling index of primitive digraphs［J］．Computers and Mathematics with Applications，2010(60)：706-732．