双转子－支承系统动力学特性的有限元分析

缪 辉，王克明，赵 帅，慕 鹏

(沈阳航空航天大学航空航天工程学部，沈阳 110136)

在旋转机械的动力学特性研究中，分析的对象大多仅仅是转子本身或者转子－轴承系统。但许多理论和实验研究表明，在某些场合下，为了更好地反映旋转机械的动力学特性，应当把基座的影响考虑进去，研究整个转子－支承系统［1］。由于基座本身是具有弹性的，基座上各个支承之间又是耦连的，若忽略基座的影响，可能在工作转速范围内出现基座－转子耦合系统的内共振［2］，如汽轮发电机组的轻型基础对转子－轴承系统动力特性的影响，具有端盖轴承的发电机定子对转子的影响，机匣对航空发动机转子的影响都有类似情形，因此考虑基座对转子系统的动力特性具有十分重要的意义。

目前国内运用有限元的方法对于整个转子－支承系统的研究尚处于发展和深入阶段，该方面的研究参考文献很多［2－5］，但大都考虑的是单转子系统。本文用有限元的方法建立了一个双转子－支承系统的有限元模型，研究了整个双转子－支承系统在弹性基座作用下的临界转速、主振型和不平衡响应。

1 双转子－支承系统结构模型

本文以如图1所示的双转子－支承系统为研究对象。该系统由内轴、外轴、圆盘、轴承(座)、支撑板以及底座组成。内转子和外转子通过轴承与底座上的3个支撑板联接，轴承1、2和4分别安装在支撑板的轴承座孔中，这3个轴承为转子提供径向的约束，轴承3为联接内转子和外转子的中介轴承，内转子和外转子上各有2个圆盘。内、外转子都是完全轴对称的，几何结构参数如表1所示，基座主要由支撑板和底座构成，其结构参数如表2所示。

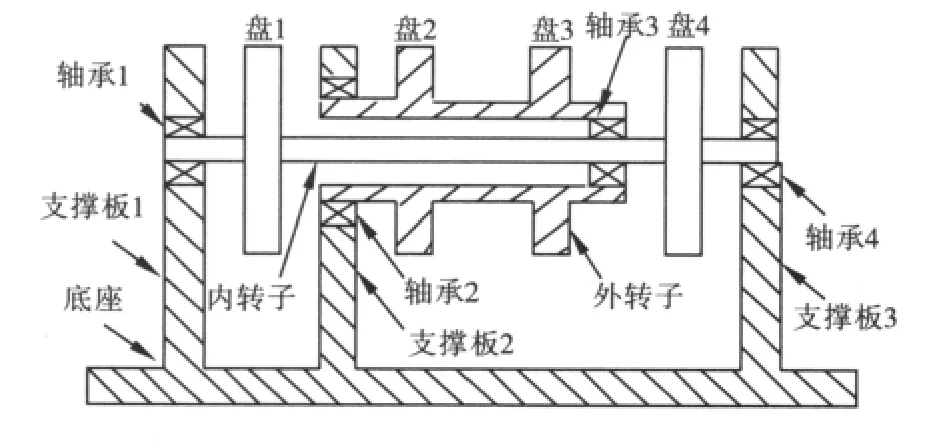
图1 双转子－轴承－基础系统结构模型

表1 内、外转子的结构参数(m)

表2 基座的结构参数(m)

2 双转子－轴承系统有限元分析

本文用有限元法分别对不考虑基座作用的双转子－轴承系统和考虑弹性基座的双转子－支承系统的动力学特性进行了计算和分析。建立的双转子－轴承系统的有限元模型如图2所示。转子部分全部采用六面体划分网格，其中节点数为16105，单元数为11585，网格质量的各项指标均达到计算精度的要求。转子部分采用的单元类型为SOLID185，轴承采用 COMBIN14单元模拟。SOLID185用于构造三维实体结构，单元通过8个节点来定义，每个节点具有3个自由度，分别为沿x、y、z方向的平移，单元具有超弹性、应力刚化、蠕变、大变形和大应变的能力，单元结构如图3所示。COMBIN14具有一维、二维或三维应用中轴向或扭转的性能。轴向的弹簧－阻尼器选项是一维的拉伸或压缩单元，它的每个节点具有3个自由度，分别为沿x、y、z方向的平移。

轴和盘的材料属性为:杨氏模量E=2.1×1011Pa，密度 ρ=783 kg/m3，泊松比 μ =0.3。坐标轴z轴方向是旋转轴方向，假设轴承是各项同性的，Kxx=Kyy，Kxy=Kyx=0，且不记阻尼的影响，轴承的刚度系数如表3所示。外转子对内转子的转速比为1.5。

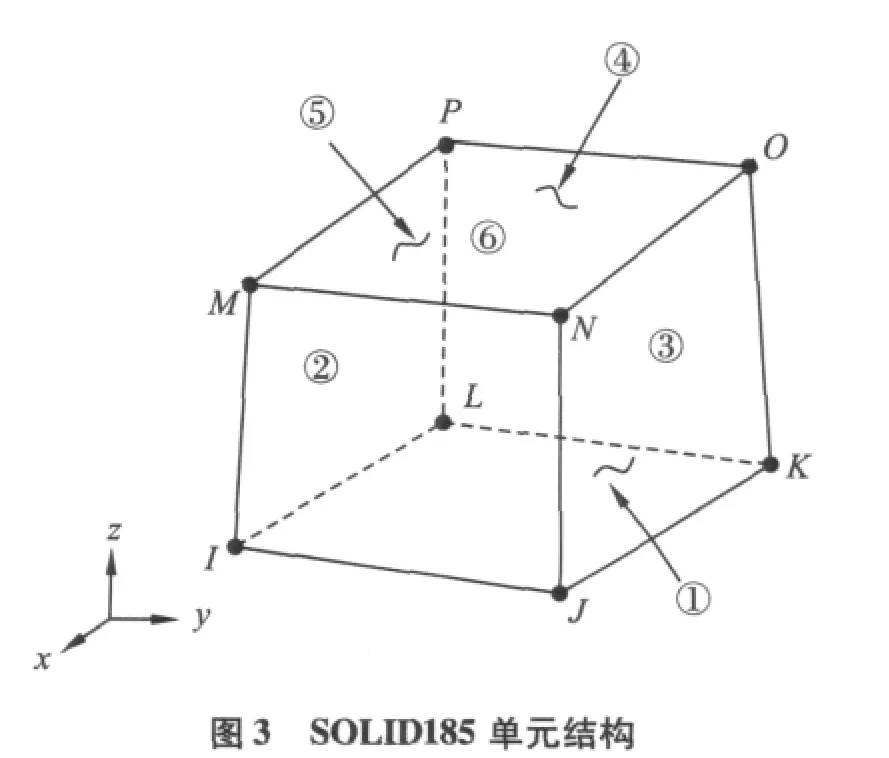
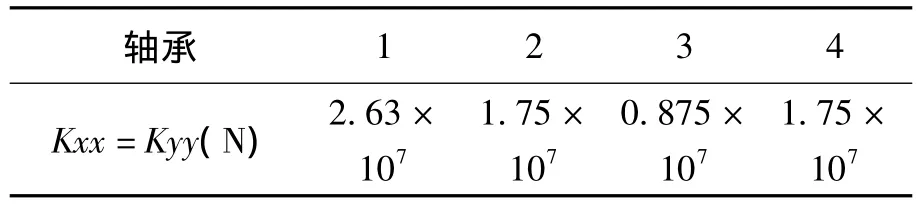
表3 轴承刚度

2.1 临界转速和主振型

用有限元法计算双转子系统的临界转速，每一阶临界转速都可能出现2个值，一个是以内转子为主激励的临界转速，另一个是以外转子为主激励的临界转速。以第一阶临界转速为例:当内转子和外转子以同一进动频率进动时，若此时内转子的自转转速等于内、外转子共同进动的频率，则称此时内转子的转速为“内转子为主激励的第一阶临界转速”;若此时外转子的自转转速等于内、外转子共同进动的频率，则称此时外转子的转速为“外转子为主激励的第一阶临界转速”。

在针对不同角速度的多载荷步模态分析中，通过Campbell图解可获得固有频率解。在ANSYS中可通过命令(PRCAMP)输出受同步力或异步力时的临界转速，临界转速位于频率曲线和附加曲线F=kω的交点。由于临界转速由Campbell图解得到，因此精确度取决于Campbell图解的质量。

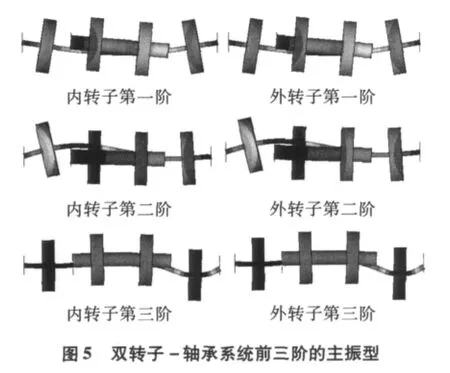
计算得到的 Campbell图如图 4所示，由Campbell图可得:以内转子为主激励的前三阶临界转速分别为1 265 rpm、3 885 rpm和9 159 rpm;以外转子为主激励的前三阶临界转速分别为1 120 rpm、3 654 rpm和9 157 rpm。内、外转子为主激励的前三阶的主振型如图5所示，图的左半部分是内转子为主激励的主振型，右半部分是外转子为主激励的主振型。

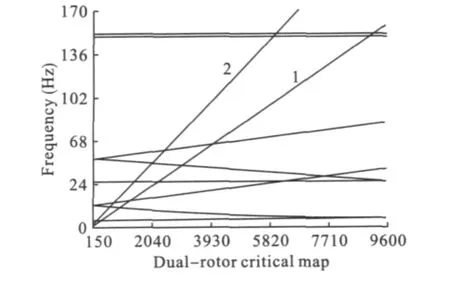
图4 双转子系统Campbell图

2.2 不平衡响应

文献［6］采用伪模态综合法计算了复杂转子系统的不平衡响应。本文用ANSYS谐响应分析中的完全法可以求出转子系统受到不平衡质量或同步旋转的激振力作用下的不平衡响应，该方法又称为同步响应法。采用分别在内转子和外转子上加同步激振力的方法，通过谐响应分析得到激振力与内转子同步时双转子系统中的2个节点(盘3上的节点与和盘4上的节点)对应的幅频特性曲线(图6)和激振力与外转子同步时双转子系统中同样的2个节点的幅频特性曲线(图7)。系统的结构阻尼设为0.01，激振力的频率范围为0 ～200 Hz。

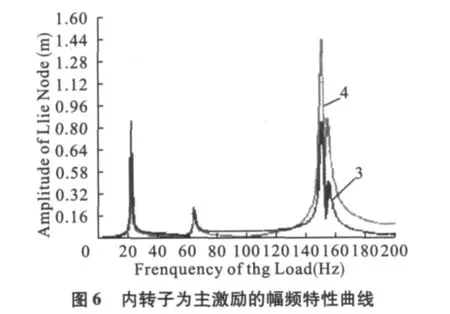
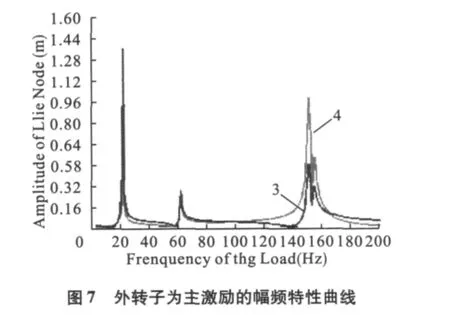
由图6可知:以内转子为主激励时，在频率为0～200 Hz的范围内，盘3和盘4分别在21 Hz、63.5 Hz、150 Hz和154 Hz处发生共振。由图7可知:以外转子为主激励时，在频率为0～200 Hz的范围内，盘3和盘 4分别在 20 Hz、60.5 Hz、150 Hz和154 Hz处发生共振。对比图6和图7可得:

(1)以内转子为主激励时，外转子上盘3在第一、三两阶临界转速下的振幅基本保持一致;以外转子为主激励时，内转子上盘4在第一、三两阶临界转速下的振幅基本保持一致;

(2)无论是以内转子还是以外转子为主激励，对盘3和盘4在第二阶临界转速下的振幅影响不大。

3 双转子－支承系统有限元分析

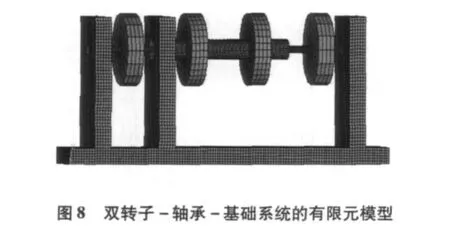
考虑弹性基座的双转子－支承系统的有限元模型如图8所示。该模型共有节点数为53574，单元数为42038。内、外转子和基座采用 SOLID185单元，轴承采用COMBIN14单元模拟，各轴承的刚度系数如表3所示。转子与底座的材料参数为:杨氏模量E=2.1×1011Pa，密度ρ=783 kg/m3，泊松比μ=0.3，外转子对内转子的转速比为1.5。对该系统中基座的接地面施加位移约束，约束其所有自由度。

3.1 临界转速和主振型

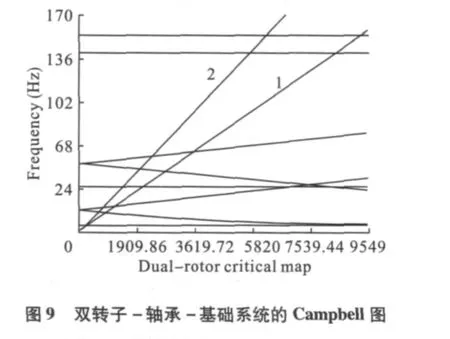
对图8中的双转子－支承系统的临界转速进行计算得到的Campbell图如图9所示。由图9可得:以内转子为主激励的前三阶临界转速分别为:1 238 rpm、3 791 rpm和8 508 rpm;以外转子为主激励的前三阶临界转速分别为:1 173 rpm、3 571 rpm和8 505 rpm。内、外转子为主激励的前三阶的主振型如图10所示，图的左半部分是内转子为主激励的主振型，右半部分是外转子为主激励的主振型。

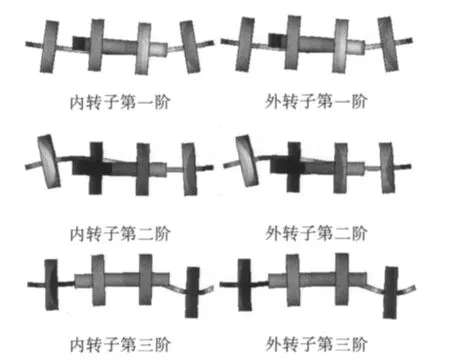
图10 双转子－支承系统前三阶的主振型

3.2 不平衡响应

同样求解激振力与内转子或外转子同步时盘3和盘4上的2个节点(与图6中的节点相同)的不平衡响应。系统的结构阻尼设为0.01，激振力的频率范围为0～200 Hz。激振力与内转子或外转子同步时的幅频特性曲线如图11和图12所示。

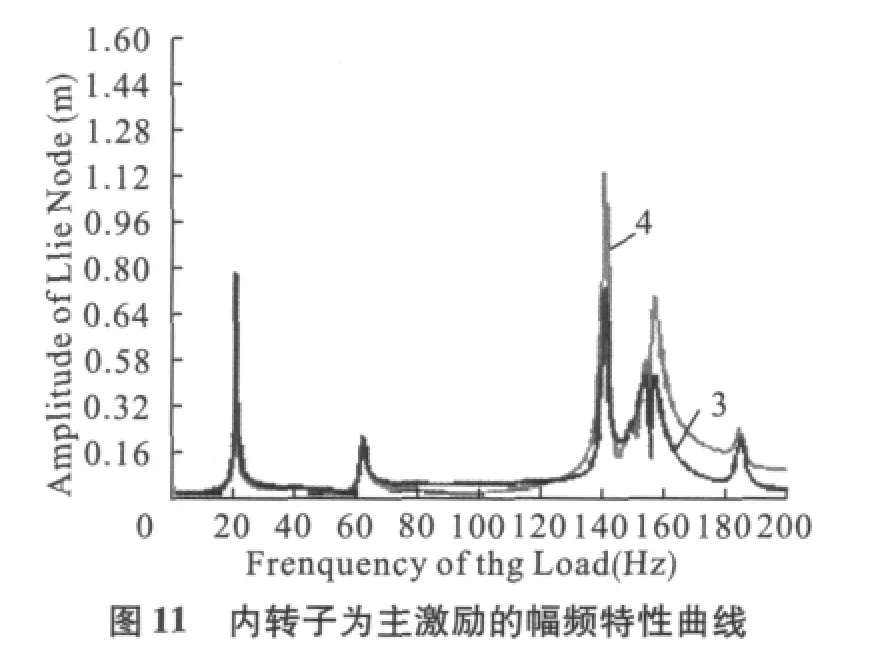
由图11可知:以内转子为主激励时，在频率为0～200 Hz范围内，盘3和盘4分别在20.5 Hz、62 Hz、141 Hz、154.5 Hz、157 Hz 和 185 Hz 处发生共振。由图12可知:以外转子为主激励时，在频率为0～200 Hz范围内，盘3和盘4分别在19.5 Hz、59.5 Hz、141 Hz、152.5 Hz、155.5 Hz、165.5 Hz和195.5 Hz处发生共振。对比图11和图12可知:

(1)以内转子为主激励时，外转子上盘3在第一、三两阶临界转速下的振幅基本保持一致;以外转子为主激励时，内转子上盘4在第一、三两阶临界转速下的振幅基本保持一致;

(2)无论是以内转子还是以外转子为主激励，对盘3和盘4在第二阶临界转速下的振幅影响很小;

4 计算结果对比分析

4.1 临界转速和主振型对比

将不考虑基座作用的双转子系统和考虑弹性基座的双转子系统的前三阶临界转速进行对比如表4所示，由表4可知:考虑弹性基座的双转子系统的前三阶临界转速比不考虑基座作用时低，这主要是由于考虑弹性基座后，系统的总刚度减小，且系统的总质量增大，因而降低了系统的临界转速;弹性基座对系统第三阶临界转速的影响要比第一、二两阶的影响高，第一、二两阶临界转速约降低了2%，第三阶临界转速约降低了7%，在这两种情况下，双转子系统前三阶的主振型(图5和图10)也发生了变化。

4.2 不平衡响应对比

对比图11和图12可知，考虑弹性基座后双转子系统在0～200 Hz范围内临界转速的个数增加了，且主要出现在155 Hz～200 Hz范围内，这主要是因为在弹性基座作用下，系统的临界转速降低了，使系统大于200 Hz的临界转速降低到了155 Hz～200 Hz范围内。将图6和图11，图7和图12进行对比发现:考虑弹性基座后，盘3和盘4在临界转速下的振幅比不考虑基座作用时要低;弹性基座对盘3和盘4在第一、二两阶临界转速下的振幅影响较小，最大相对误差为－11.92%，对第三阶临界转速下的振幅影响较大，最大相对误差为－31.41%。对于盘3和盘4上同一个节点来说，在各临界转速下考虑弹性基座和不考虑基座作用时振幅的相对误差并不是保持一致的，因此考虑弹性基座后转子系统的主振型也发生了相应的变化。

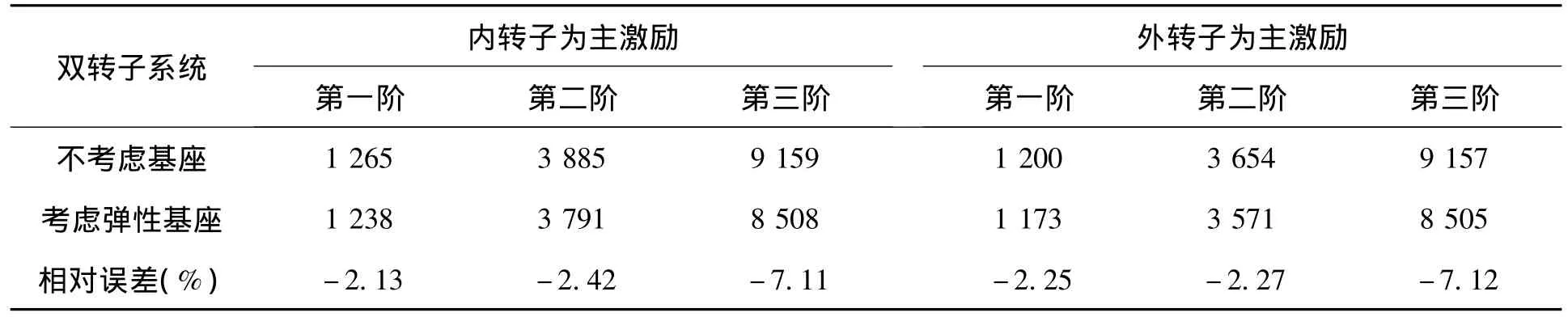
表4 基座对双转子系统临界转速的影响

5 结论

本文建立了双转子－支承系统的有限元模型，用有限元法计算和分析了弹性基座对双转子－支承系统的临界转速、主振型和不平衡响应的影响。计算结果表明:与不考虑基座作用的双转子－轴承系统相比，考虑弹性基座的双转子－支承系统的前三阶临界转速降低了，弹性基座对第一、二两阶临界转速影响较小，对第三阶临界转速影响较大;在弹性基座作用下，系统的主振型也发生了相应的变化;在0～200Hz范围内，弹性基座使双转子－支承系统中临界转速的个数增加了，增加的临界转速主要出现在155～200 Hz范围内;弹性基座降低了系统在临界转速下的振幅，且对第一、二两阶临界转速下的幅值影响较小，对第三阶临界转速下的幅值影响较大。

［1］钟一谔，何衍宗，王正，等.转子动力学［M］.北京:清华大学出版社，1987.

［2］徐敏，廖明夫，刘启洲.基础－转子系统内共振研究［J］.机械科学与技术，2002，21(1):55 －57.

［3］张薇薇，胡业发.磁悬浮轴承－转子－基础系统的耦合动力学模型［J］.机械设计与制造，2008(11):137－139.

［4］梅德庆，何闻，沈润，等.大型汽轮发电机组框架式基础的动力特性研究［J］.动力工程，2001，21(1):1014－1018.

［5］杨丰产，徐培民，马云吉.转子－轴承－基础系统有限元模态分析［J］.机械工程师，2009(3):69－71.

［6］朱芸.复杂转子系统不平衡响应计算的伪模态综合法［J］.江南学院学报，2001，16(2):21 －25.

［7］缪辉，王克明，翟学，等.反向须转双转子系统动力学特性的有限元分析［J］.沈阳航空航天大学学报，2011，28(4):27 －32.

［8］缪辉，王克明，艾书民，等.双转子系统临界转速的有限元分析［J］.沈阳航空航天大学学报，2011，28(5):27－31.