基于分形理论的制造信息系统的结构建模研究

张小花，陈 玮

ZHANG Xiao-hua1, CHEN Wei2

（1.仲恺农业工程学院 机电学院，广州 510225；2.广东工业大学 自动化学院，广州 510640）

0 引言

分形理论是非线性科学的生长点之一，在自然科学、社会科学等方面得到了大量应用。与数学上构建的严格意义上的分形图形不同的是，现实系统的分形结构都是统计意义上的自相似的，它们是随着时间的发展不断演化形成的。现实系统的分形结构的产生有两个条件：一是基本单元，二是非线性动态迭代，而这些正是先进制造信息系统本质所在。当前的制造信息系统发展的模式就是靠有丰富层次的基本实体以及系统内部自组织的作用，从而建立起一个开放的、有层次结构的耗散系统，制造信息系统本身是一个非线性动力学系统。因此，分形理论可以用来研究制造信息系统的各层次之间的功能和结构的自相似性。尽管作为一种全新的数学工具，分形理论诞生的时间还很短，在制造企业的建模方面的应用还处于探索阶段，它在制造业的供应链[1～3]、企业网络流量的分析[4,5]以及机械故障诊断[6]方面都得到了成功的应用。对于制造系统来说，分形理论既是一种建模的技术方法，也是一种思想和理念。将分形理论引入到制造信息系统的建模过程中，分析了制造信息系统中存在的分形特征，提出了基于分形理论的制造信息系统的结构建模方法，以动态控制元结构为生成元，找出系统分形结构的构成规则，并通过一个实例来验证该方法构建的制造信息系统分形结构模型。

1 基于分形理论的制造信息系统结构建模方法

1.1 制造信息系统的分形特征

无论从企业的组织模式还是信息流的观点来看，制造信息系统在各个层次之间都有统计意义上的自相似特性。制造信息系统存在不同尺度的自相似特性。所谓不同尺度的自相似，是指某种结构或过程的特征从不同的时间尺度、空间尺度或任何其他合理定义的尺度来看是相似的，可以看成该系统(或结构)的局域相似或结构与整体相似，如果系统包含不同的层次，则不同层次(尺度)上都存在相似。研究制造信息系统的分形特征，主要是研究其在不同尺度的自相似性。

1.1.1 层次结构的相似性

用一般系统结构理论来分析制造信息系统，系统中包含子系统，子系统又可以分为许多层，直到找到基本层次才不再划分，同时，在基本层次里又可以找出基本结构单元。如图1所示，一直按照单元和规则分下去，最基本的单元结构为动态控制元结构。以一般系统结构论的观点为尺度，可以用分形集合的方法对上述的制造信息系统进行描述。公式（1）是以元结构为分形元的自仿射分形的表达方式。

式中，＂M-”前缀表示制造信息系统，＂S-”前缀表示子系统，“SN-”前缀表示第N个子系统。在上式中，每个子系统之间同样具有相似的运行结构或分析方法，形成了一种嵌套的分析方法。上述组成制造信息系统的各级嵌套的子系统都是具有一定独立性的自主的单元，在结构上、功能上有相对的内部完整性，并与其周围环境有着相对明确的边界。

1.1.2 时间尺度的相似性

在制造企业的创业初期，企业的信息系统是无序的，由于业务的发展，资源的整合，逐渐由准平衡态走向非平衡态，非平衡态是企业系统有序之源。远离平衡态是耗散结构形成的前提条件。一个充满活力的企业系统，必定是一个有差异、非平衡的系统。在准平衡态走向非平衡态时，制造信息系统的有序程度降低，无序程度增加，并且自组织发生作用，其自组织的关键是大量子系统的共存和非线性相互作用。当企业意识到企业的无序可能对企业带来的危害时，就会采取一系列的措施，使企业增加有序，减少无序，这时产生新的有序结构。有序度增加导致突变是由涨落来完成的，企业系统中的各要素时刻处于涨落的动态变化中，从而启动非线性的相互作用，使系统发生质的变化，跃迁到一个新的稳定有序状态，形成耗散结构。因此涨落是一种启动力，可以导致有序。在有序到一定程度就会使整个制造信息系统发生突变，进入一种新的状态，这种状态就是远离平衡态的耗散结构，这是一种新的有序状态，系统不断加入负熵来提高系统的有序性。系统进入耗散结构后，制造信息系统内部的运行方式就有混沌的因素存在，这种混沌运

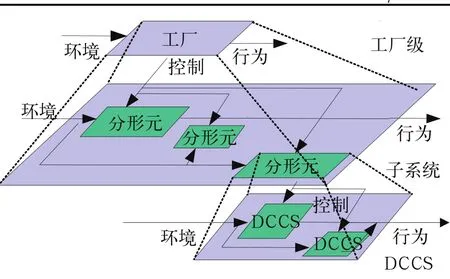
图1 结构层次的自相似性

动并不是无序的，而是看似无序的一种有序。当企业发展到了后期，系统有序性逐渐减少，无序性逐渐增加，当无序性增加到一定程度，就会使企业迅速衰落。

从时间的尺度来看，在制造信息系统的动态运行过程中，由于制造信息系统属于复杂系统，其寿命周期的演化是一个从有序到无序的过程，具体过程如图2。制造信息系统就不断遵循着这样一个演化过程，在不同的时间段，它是自相似的，满足时间分形的特征。

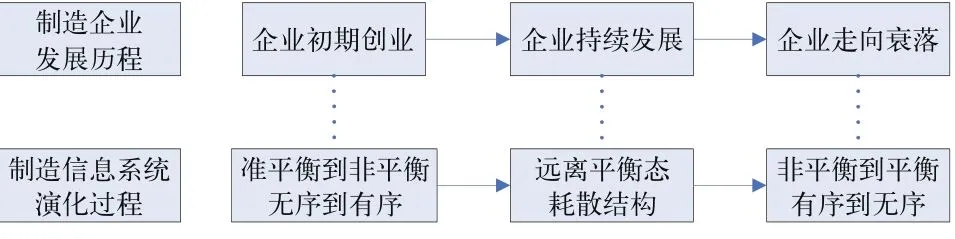
图2 制造信息系统的演化过程

1.2 制造信息系统的分形元结构提取

根据分形理论，复杂系统的内部各单元之间存在统计意义上的信息同构，结构存在不同层次的自相似，而一个确定性分形是一个迭代函数的不变集。制造信息系统的结构可以通过相似的简单的元结构和相应的规则进行迭代来生成，动态控制元结构是构建系统过程中提取出来以满足对系统静态结构和动态运行特性分析并实行系统快速重组为目标的单元。它必须具有以下性质：

通用性：动态控制元结构的功能是抽象的，结构是具体的，所以动态控制元结构可能对应不同的功能实体，成为表示某些不同环节的通用模块。

典型性：由于希望用尽量少的结构和规则来表达整个系统，所以动态控制元结构的功能和控制特性必须具有典型性。

自治性：动态控制元结构可以在没有外界参与的情况下根据自身的状态和行为、内部状态和环境信息自主地独立执行任务。

可重构性：动态控制元结构作为一个独立模块，在外界环境变化时，可以快速组建系统。

易操作性：作为一种建模手段，动态控制元结构的结构必须简单，易于操作，以便降低系统构建的复杂性。

根据上面的描述得出动态控制元结构的框架模型，如图3所示。

由于建模的目标是研究制造信息系统的演化过程，因此对元结构进行抽象，可把它看做是一个“三态”结构：准备状态、工作状态和故障状态。任何单元和设备都可以简化，因此可用元结构的三角形作为生成元，选取适当迭代规则进行迭代生成分形总图。

图3 动态控制元结构及与环境的交互

1.3 制造信息系统的分形规则

用分形算法实现制造信息系统结构模型的方法，很象制造信息系统的生长模式。它的实现步骤如下：

1）确定基本生成元，并选取好制造信息系统的层数作为迭代次数；

2）给定映射函数；

3）开始迭代，直到满足要求。

另外，针对制造信息系统的实际结构，在构建实际系统的时候还要遵循下面的规则。

规则1：迭代的次数取决于系统的层次，当到达系统的支配层次时，实现最后一次迭代，此时最后一层中的节点都可以看作是元节点。系统结构是开放的，不同的系统迭代次数不一样。随着企业经营过程的发展，其实体与规则的数量与层次也不断地增加、提炼与细化，从而通过基本实体与规则的相互作用，构成更新的功能，以适应新的环境变化的需求。

系统的组成部分是由若干更小的部分组成，系统具有结构层次性是系统实现某种系统行为或功能的基础和客观要求。在制造信息系统的目标分解中，一般它的层数都是由目标分解的粒度决定的。在系统研究中，正确把握和理解系统的结构层次是理解和揭示系统运动及规律的基础。

规则2：分形图形中的结构可能在实际系统中找不到对应的实体，这种结构称之为空结构，它只起传递作用。空节点可以和它同处一层的节点看作同一节点，合并在一起，从而与实际系统对应起来。

规则3：同一层次的节点之间是否存在关系可以根据实际系统的关系环而定，当它对应的节点表示该层的某个单元时，那么它是否与该层其它节点相连要看实际系统中该单元与其它单元的关系。

由一般系统结构论可知，关系环是系统复杂性之源。制造信息系统是个复杂系统，它不仅在纵向上与下层有联系，在同一层次之间，各个单元之间还有相互作用。这个相互作用就是在该层的关系环。

规则4：各个分形结构之间可以通过层次结构连接方式组成新的分形结构。

层次结构是复杂系统的上层结构，用Gh表示，与下层结构，用Gl表示，如果把Gh的能控事件定义为Gl的某标识运行事件串Lm(Gl)，则称Gh与Gl构成层次结构。

规则5：只有当相应事件触发，才能激励下一个状态的发生，该状态的输出事件会导致另一个实体单元的状态改变，从而新的单元加入到系统中，这个新单元在运行过程又会产生新的事件，依此循环，直到满足构建目标为止。

以三角形作为动态控制元结构的抽象结构，可以把节点看作状态，连接节点的边看作事件，那么上一个节点的输出事件一定是后一个节点的触发事件，且状态转移的条件得到满足，才会进行下一次迭代。

规则6：要满足制造信息系统的功能特性，则在结构上必须保证信息的可达性。

规则7：在构建系统的时候，制造信息系统的不同层次之间以及同一层次的不同单元之间存在交互，这需要接口发挥作用：选择交互对象、传递信息和实现状态映射。而接口实现上述功能是在宏观序参量的伺服作用下进行的，它根据各个序参量的权重系数、生产需要和一定的管理规则来具体选择哪个单元。

2 构建系统结构实例

本文以Agent系统作为制造信息系统的建模框架。制造信息系统是为了完成某一生产任务而设计的人造复杂系统，因此构建系统结构，应根据具体生产任务和环境的存在要素进行任务分解产生任务树，分析任务树构成，构建层次结构的多Agent系统拓扑图。

按照实际系统要完成的任务，可以把任务按垂直和水平两个方向进行任务分解。垂直任务又看作子任务，而水平任务是其兄弟任务。分解所得的子目标分为“或”子目标和“与”子目标。

本文采用自上而下的分解方法，通过不断细化和分解系统的生产任务，直到系统的最底层为止，形成一个有层次的树型结构。制造信息系统由销售、生产管理、仓库和财务单元实体组成，并且每个单元实体看作一个Agent。每个单元实体又按照功能继续划分下去，实际系统的任务树型结构如图4。数字0、1、2、3、4、5、6分别表示销售、财务、生产管理、仓库、计划、采购和生产单元。

由于任务树结构只能表达出系统的任务之间的关系，要完整的把系统的各个单元之间的关系表达出来，则要画出系统的多Agent拓扑图。在图4的基础上，根据各个单元实体之间的拓扑关系，省略销售和仓库单元的底层任务，如图5。图中每个单元实体的数字标注都与图4一一对应。这是一个系统的拓扑关系图，只是表达单元之间的联系，不能表达整个系统的层次关系。

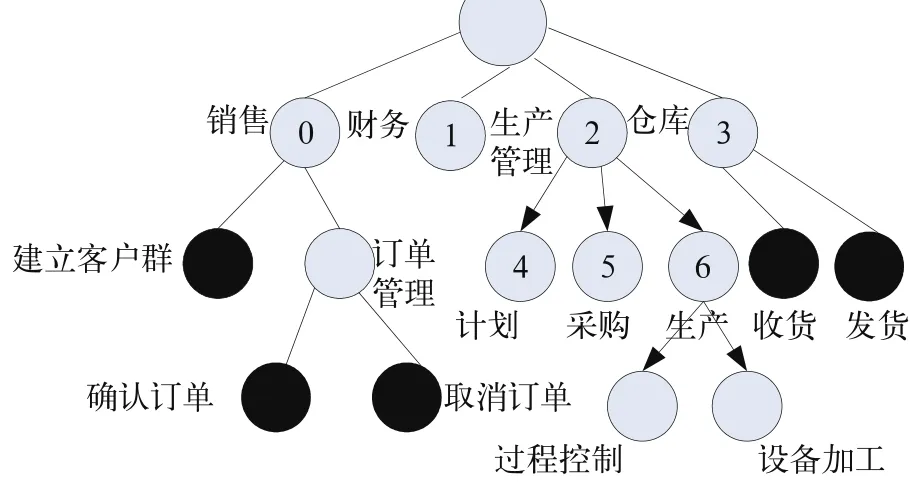
图4 制造信息系统任务树

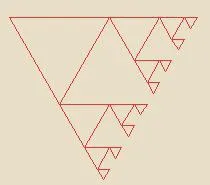
图6 迭代三次的分形图形

利用分形的构建规则，可以将图6在以动态控制元结构的三角形作为生成元，选取适当迭代规则进行迭代生成分形总图。这里的迭代规则是下一层的图形生成是以当前该层的n个顶点为起始点，自顶向下再派生出n个三角形。本文应用Delphi软件来进行迭代图形的构建，由此迭代规则迭代三次后得出的分形图形如图6。从图6可以看出，该制造信息系统的结构模型是一个典型的分形图形，在此基础上，可以利用分形的相关知识对其进行功能特性和控制特性分析。

3 结束语

分形理论在制造信息系统的结构建模的研究还处于探索阶段，本文应用分形理论来研究制造信息系统的各层次之间的功能和结构的自相似性。在此基础上，以动态控制元结构为分形元，

按照一定的迭代规则，构建出系统的结构总图，

从而实现对制造信息系统的结构建模。该结构模型为以后进行模型的功能特性和结构特性分析奠定理论基础。

[1] Patrick Walsh,Philippos Koutsakas,Apostolos Vontas,Adamantios Koumpis.Building enterprise-wide information supply chains based on the fractal concept[J].Integrated Manufacturing Systems.2003.5(14):397-408.

[2] Towill D R.Management, Industrial dynamics modeling of supply chains[J].Logistics Information.1996,9(4):43-56.

[3] 周建频,杜文.制造业分形供应链的适应与协调[J].控制与决策.2005.4(20):459-463.

[4] 丛锁,韩良秀,刘岩,高传善.基于离散小波变换的网络流量多重分形模型[J].通信学报.2003,5(24):43-48.

[5] 王成,刘金刚,刘汉武.网络中突发业务自相似建模及其Hurst系数估计[J].计算机工程.2006,2(32):101-103.

[6] 汪慰军,陈进,吴昭同.关联维数在大型旋转机械故障诊断中的应用[J].振动工程学报.2000,13(2):229-234.