Proteus仿真环境下的PID参数整定及其应用*
王清 肖忠 姚菁
(广州大学机械与电气工程学院)
1 引言
控制器的设计通常是在MATLAB仿真平台上进行。因为MATLAB有强大的数值计算和图形功能,在控制方面,有时域分析、根轨迹分析和频率特性分析等多种辅助分析设计工具可以利用。但是在实际系统中往往是将控制算法下载到微处理器中使用,控制算法不用MATLAB语言,而用C语言。这样从仿真到应用,就需要一个编程语言的转换过程,但仿真时没有微处理器、DA转换器等硬件,不能直观地反映所需硬件在系统中的作用。另外,AD、DA等硬件在实际使用中有位数、精度、输出范围的限制,运算电路的加减运算或比例运算也是在一定范围内进行的,超出则会限幅,这些因素都不同程度地制约着控制器的工作效果,都应在仿真中尽量体现出来。近年来在单片机教学中逐渐流行的Proteus 仿真软件可以弥补这种不足。
Proteus ISIS是英国Labcenter公司开发的电路分析与实物仿真软件,其主要特点有:① 实现了单片机仿真和 SPICE电路仿真相结合,具有模拟电路仿真、数字电路仿真、单片机及其外围电路组成系统的仿真,还有各种虚拟仪器,如示波器、逻辑分析仪、信号发生器等;② 支持主流单片机系统的仿真,目前支持的单片机有8051、AVR、PIC12、PIC16、PIC18等系列以及各种外围芯片;③ 提供软件调试功能,支持第三方的软件编译和调试环境,如 ATMEL公司推荐的第三方C编译器ICCAVR等软件;④ 具有强大的原理图绘制功能。因此可以考虑尽量利用Proteus软件进行仿真,避免上述MATLAB语言到C语言的转换工作,提高系统设计的效率;软、硬件仿真同时进行,使控制系统构成更加接近实际,反映信息更加全面。本文以PID控制器参数整定及其应用为例具体加以说明。
2 Proteus中的控制系统仿真模型与分析工具
① 用于被控对象的模型
Laplace Primitives大类下:微分、积分模型;多项式、零极点等多种形式的一阶、二阶模型(1 ord:poly等);非线性模型:带死区的放大器(NL:AMP DZ)、带饱和的放大器(NL:AMP SAT)、带滞环的放大器(NL:AMP HYST)等;延迟环节模型(OP:DELAY)。
Electromechanical大类下:简单直流电机(MOTOR)、无刷直流电机(MOTOR-BLDCM)、伺服电机(MOTOR-SERVO)、步进电机(MOTOR-STEPPER)等模型。
② 用于控制器部分的模型
PID调节器(CTRL:PID)、超前校正(CTRL:ADVANCE)、滞后校正(CTRL:DELAY)。
③ 用于传感器部分的模型
Resistors大类、NTC子类下多种热敏电阻传感器模型;Transducers大类下光敏电阻;数字温度传感器18B20、压力传感器mpx4115等。另外,可根据需要模拟传感器,如用压控电阻VCR模拟PT100热电阻。设定该模型的On Voltage为200V,On Resistance为175.6Ω,Off Voltage为0V,Off Resistance为100Ω,则VCR恰好可表示在0℃~200℃范围的阻值―温度关系[1]。
仿真时,可利用图表模式(Graph Mode)下的模拟分析“ANALOGUE ANALYSIS”功能以图形化方式显示记录仿真分析结果,图表还可缩放,方便设计者进行细节分析。使用模拟分析时,先在要观察的点上设置电压探针,再把探针名添加到 ISIS的GRAPH|Add Trace项和“ANALOGUE ANALYSIS”的Add Transient Trace 项中即可。
3 PID参数整定及临界比例度法
在控制工程中,PID控制器是最早发展,并且仍然在广泛应用的控制策略之一,据统计工业过程控制领域仍有近90%的回路在应用PID控制策略[2]。因为它具有结构简单、可靠性高、稳定性好的显著特点。PID 控制器的核心问题是其参数整定问题。PID控制器参数整定的方法很多,概括起来有两大类:一是理论计算整定法。它主要是依据系统的数学模型,经过理论计算确定控制器参数,工程应用时再进行适当的调整;二是工程整定方法。利用经验公式,在控制系统的试验中进行。这种方法简单、易于掌握,在工程实际中被广泛采用。PID控制器参数的工程整定方法,主要有临界比例度法、反应曲线法和衰减法等。各种方法各有其特点,其中临界比例度法应用较多。但无论采用哪一种方法所得到的控制器参数,都需要在实际运行中进行最后调整。
设控制系统的给定值与实际输出值构成的控制偏差为e (t),将偏差按比例、积分和微分通过线性组合构成PID控制量u (t),对被控对象进行控制,则控制量可描述为:
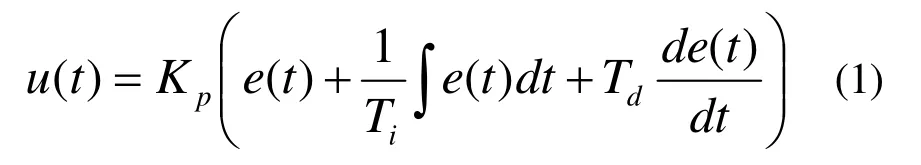
式(1)中,Kp为比例系数;Ti为积分时间常数;Td为微分时间常数。临界比例法是借助实验由经验公式得到控制器的近似最优整定参数。应用方法是:在闭合的控制系统里,将控制器置于纯比例作用下,从大到小逐渐改变控制器的比例增益,直到系统输出对输入的阶跃响应出现等幅振荡。此时的比例增益被称为临界增益 Ku,相邻两个波峰间的时间间隔为临界振荡周期 Tu。之后通过表1中的经验公式,计算出控制器各个参数。
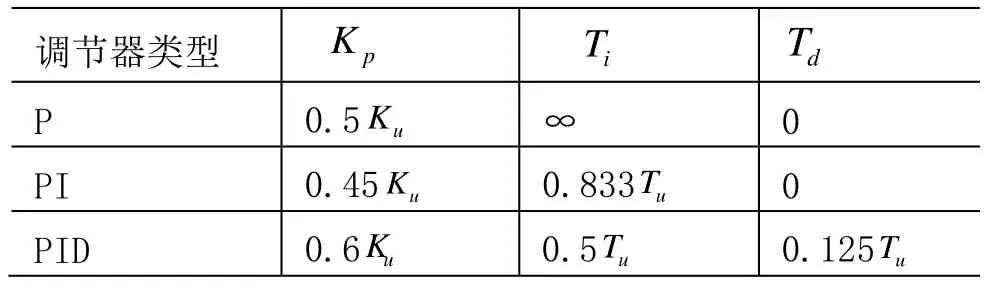
表1 临界比例度法参数整定公式
4 仿真实例及临界比例度法
① 搭建系统的Proteus仿真原理图,如图1所示。图1中,输入阶跃信号由程序给定,PID控制算法由ATMEGA128微处理器中程序实现,D/A转换器选用DAC0832,被控对象则由Laplace转换模型中的积分和一阶模型串联组成,微处理器输出的0V~5V误差控制信号经由DAC0832、运放 U1、U2组成的转换电路变为±10V信号作用到被控对象上,之后由运放U5、U6组成的转换电路转换成0V~5V,反馈回微处理器内部的A/D转换器;此外为了直观的分析阶跃响应,用了“ANALOGUE ANALYSIS”模拟分析工具。
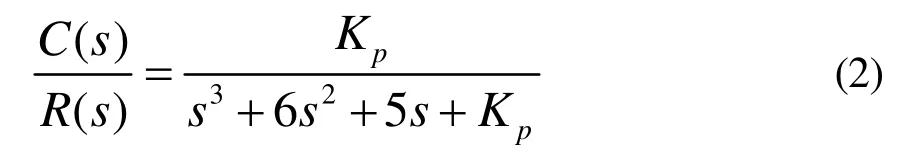
② PID控制器设计。设系统为只有比例控制的闭环系统,则闭环系统的传递函数为:由Ruth稳定判据可知,当时,闭环系统产生持续等幅振荡。将控制器置为纯比例信号,用上述Proteus仿真原理图做阶跃输入实时仿真,同样得到这一结论。
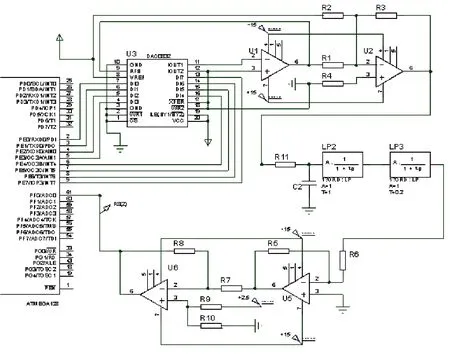
图1 Proteus仿真原理图
将振荡时对应的临界增益Ku和临界振荡周期Tu带入表1,可得PID控制器的参数:Kp=0.6Ku=18;Ti=0.5Tu=1.4;Td=0.125Tu=0.35,以此参数进行系统仿真,得阶跃响应曲线如图2所示,可见系统稳定,但超调量较大。
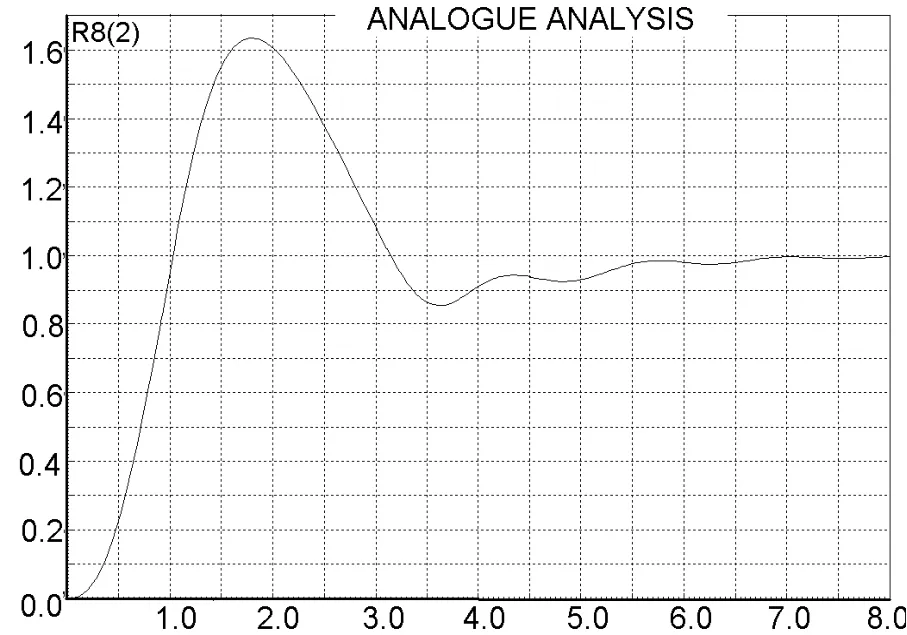
图2 基于PID控制的系统阶跃响应
减小比例作用,取 Kp=10;增大积分时间,取Ti=25;增大微分时间,取Td=0.5,得到参数调整后阶跃响应,如图3所示。此时与图2相比,调节时间基本没变,但超调量降到几乎为零,有效地改善了系统特性。对比仿真表明,临界比例度法可有效地为控制器设计提供基本参数,基于该参数的进一步调整是很必要的。Proteus提供的分析工具为调整工作带来很多便利。
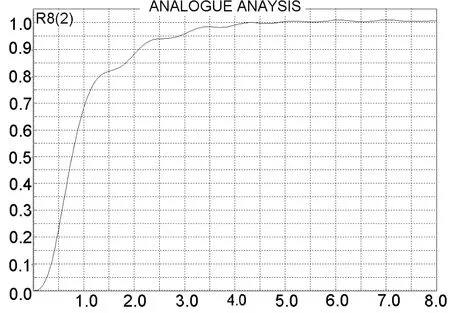
图3 调整后PID控制的系统阶跃响应
5 结论
Proteus软件强大的软硬件仿真功能为控制系统设计提供一个宝贵的开发平台。在此平台上的设计仿真,软件方面,采用实际系统将要应用的编程语言,无需转换;硬件方面,不再仅仅是数学模型的仿真,而是直接与微处理器、控制电路、控制对象最大程度地结合起来。控制系统设计开发的时间、风险、成本均可有效减少。本文基于临界比例度法的PID参数整定的应用仿真表明,在Proteus 软件环境下能够准确方便地完成控制器的设计。
[1] 丁明亮.51单片机应用设计与仿真—基于 KeilC与Proteus[M].北京:北京航空航天大学出版社,2009,222.
[2] 王伟,张晶涛,柴天佑. PID参数先进整定方法综述[J].自动化学报,2000,26(3):347-355.

