主成分分析法在SPSS软件中的操作及在河流水质评价中的应用

吉祝美，方 里，张 俊 ，马晶晶

(江苏省盐城市环境监测中心站， 江苏 盐城 224001)

河流监测一般按照GB 3838—2002《地表水环境质量标准》确定的24个基本项目进行分析，由于项目众多，要将所有项目全面评价到位显得比较困难。由于这些项目相互之间有一定的相关性，我们就可以运用主成分分析法选取少数几个互相无关的指标来代替它们进行评价。主成分分析方法(PCA法)是一种将多维因子纳入同一系统中进行定量化研究、理论比较完善的多元统计分析方法，在解决很多实际问题时取得了较好的效果[1－2]。

1 主成分分析法原理

主成分分析法是一种降维处理技术的数学变换方法，其基本思想就是设法将原来众多且具有一定相关性的指标，转化成少数几个综合指标。该方法主要研究如何通过少数几个主成分来揭示多个变量间的内部结构，即从原始变量中导出少数几个主成分，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。

进行主成分分析的主要计算步骤为[3－5]:

(1)根据研究问题选取指标与数据。

(2)进行指标数据标准化，以消除不同指标之间的量纲影响。

(3)进行指标之间的相关性判定，确定待分析的原始变量是否适合进行因子分析。

(4)确定主成分的个数m。主成分个数提取原则:①只取特征根λ＞1时对应的主成分;② 累计百分比达到80% ～85%以上的λ值对应的主成分;③根据特征根变化的突变点决定主成分的数量。

(5)确定主成分Fi的表达式。

(6)进行主成分Fi的命名。

(7)计算综合主成分值并进行评价与研究。

2 SPSS(V19.0)中主成分分析的操作

2.1 指标选择

在“分析”菜单“降维”中选择“因子分析”命令，在弹出的“因子分析”对话框(图1)中，从对话框左侧的变量列表中选择需要分析的变量，使之添加到变量框中。

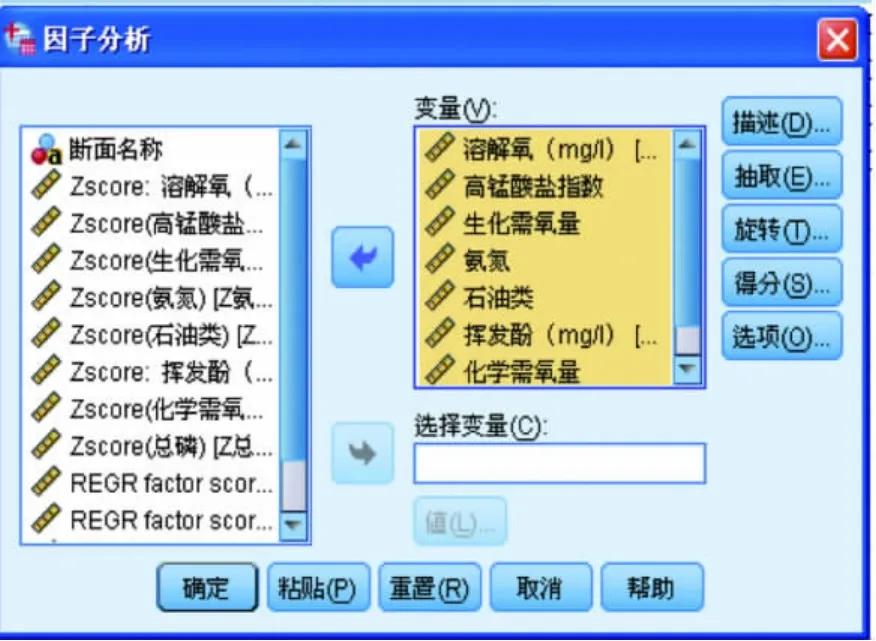
图1 “因子分析”对话框

2.2 运算

分别单击“描述”、“抽取”、“旋转”、“得分”及“选项”按钮，弹出“因子分析:描述统计”对话框(图2)、“因子分析:抽取”对话框(图3)、“因子分析:旋转”对话框(图4)、“因子分析:因子得分”对话框(图5)、“因子分析:选项”对话框(图6)，按图中显示勾选相关复选框后，单击继续按钮返回“因子分析”对话框，在“因子分析”对话框点击“确定”按钮，完成计算，SPSS很快给出计算结果(图7)。

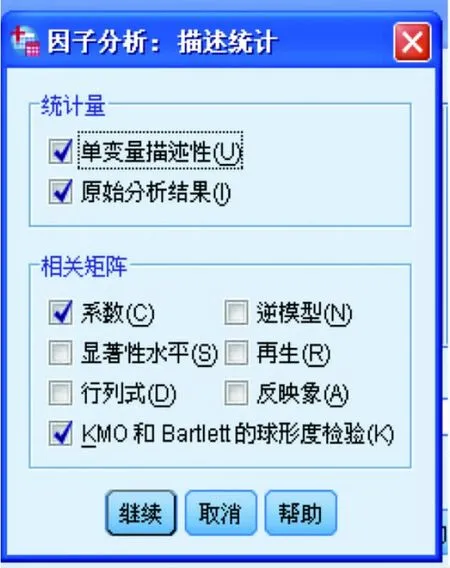
图2 “因子分析:描述统计”对话框

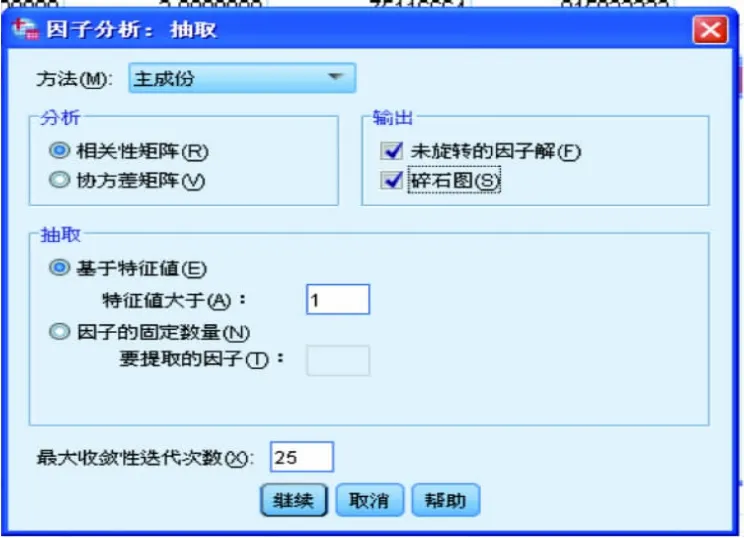
图3 “因子分析:抽取”对话框

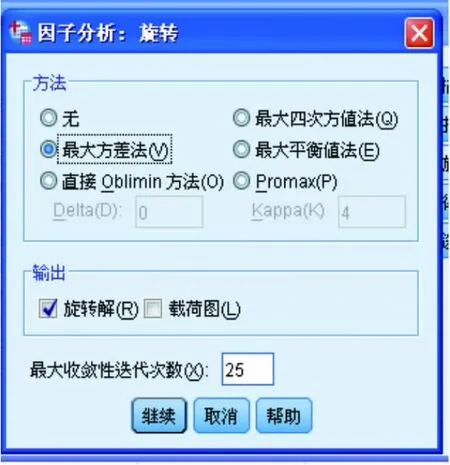
图4 “因子分析:旋转”对话框

图5 “因子分析:因子得分”对话框

图6 “因子分析:选项”对话框

图7 主成分分析的结果

2.3 指标数据标准化处理

在因子分析时，SPSS会自动对原始数据进行标准化处理，所以得到的变量都是经过标准化处理后的变量。但SPSS并不直接给出标准化后的数据，如需要得到标准化数据，则需调用描述过程进行计算。具体方法是在“分析”菜单“描述统计”中选择“描述”命令，在弹出的“描述性”对话框(图8)中，从对话框左侧的变量列表中选择需要分析的变量，使之添加到变量框中，并勾选“将标准化得分另存为变量”选项。点击“确定”后得到标准化数据。

图8 “描述性”对话框

3 主成分分析法在河流水质评价中的应用

3.1 监测点与监测指标

串场河是里下河地区与沿海垦区之间纵贯南北的人工河道。南起海安三里闸，经富安、安丰、东台、刘庄、盐城、上冈，至阜宁入射阳河，沿途穿斗龙港、新洋港、黄沙港等，是里下河地区各河(港)排水入海的总调节河道，也是里下河地区和沿海垦区的分界线。串场河基本反映了盐城市阜宁县城以南大部分水域的水质状况，所有串场河以西的河水都要与串场河交汇，对串场河的水质有一定影，串场河水质对反映盐城市水质状况有一定的代表性。共设8个监测断面开展串场河水质例行监测(图9)。2011年各断面年均值见表1。

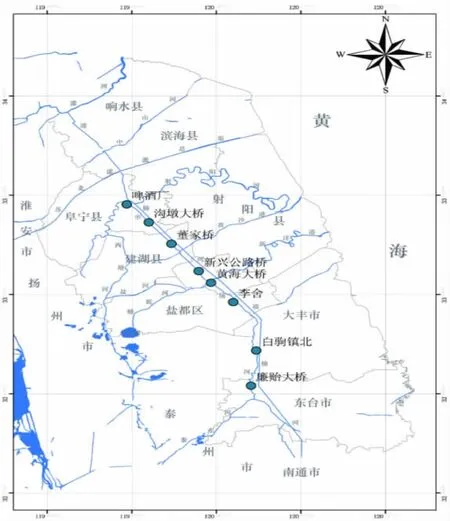
图9 监测点位示意图

3.2 评价过程

将监测数据进行标准化处理后得到的标准化数据见表2，标准化处理后各行数据平均值等于零，标准差等于1。

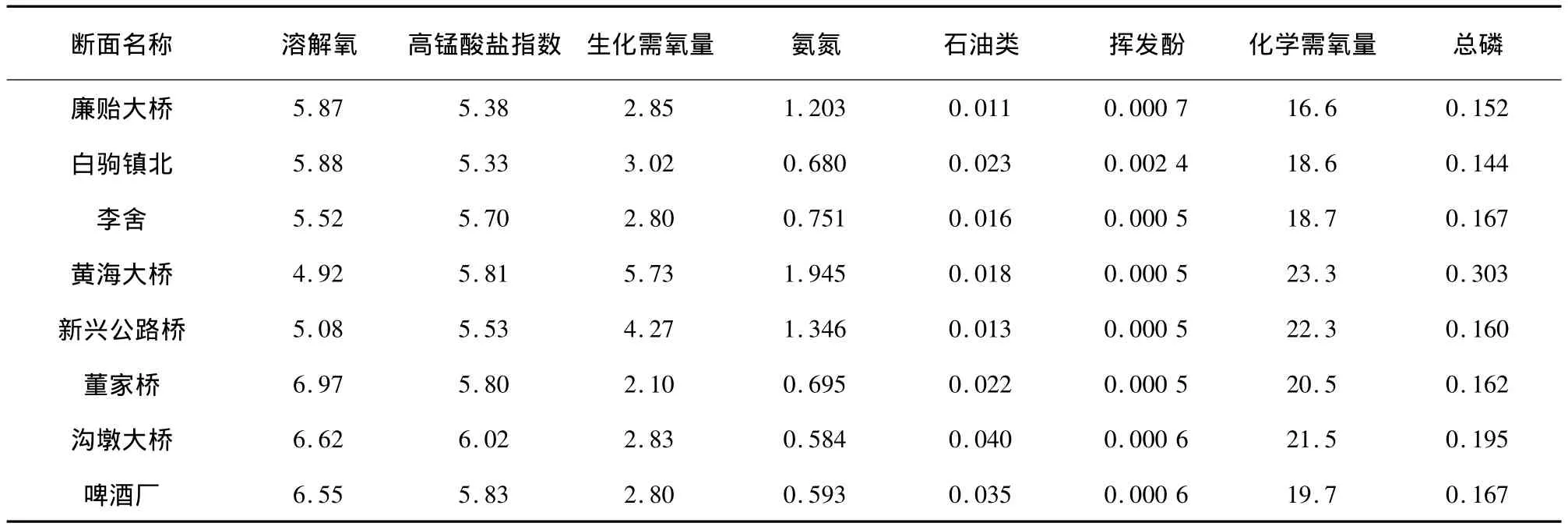
表1 2011年各监测断面8个评价指标的年均值 mg/L

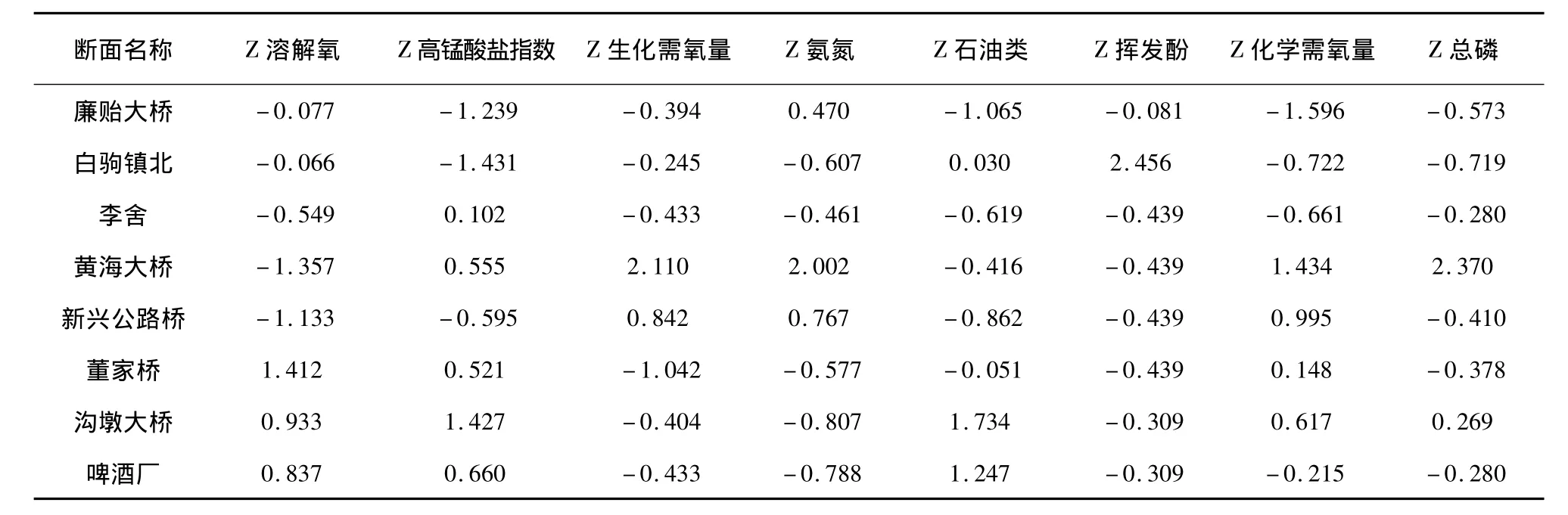
表2 标准化处理后的数据

利用SPSS软件分别对溶解氧(X1)、高锰酸盐指数(X2)、五日生化需氧量(X3)、氨氮(X4)、石油类(X5)、挥发酚(X6)、化学需氧量(X7)、总磷(X8)8个评价指标的相关系数和特征值进行分析并根据累计贡献率确定主成分个数。相关系数矩阵见图10。

从相关系数矩阵中看出，大部分相关系数大于0.3，可见许多变量之间直接的相关性比较强，证明

，他们存在信息上的重叠，则这些原始变量适合进行因子分析。生化需要量与溶解氧、氨氮及总磷有很强的相关性(其中与溶解氧成负相关)，相关系数分别达到 0.821、0.900 和 0.798。

根据主成分分析法中主成分个数选取原则，从图11可见特征值λ＞1时有两个成分:λ1=3.877，λ2=2.612，此时累计百分比达到81.111%，同时通过图12分析特征根衰减的突变，可以确定应提取2个主成分，即k=2(SPSS软件自动提取了2个主成分)。

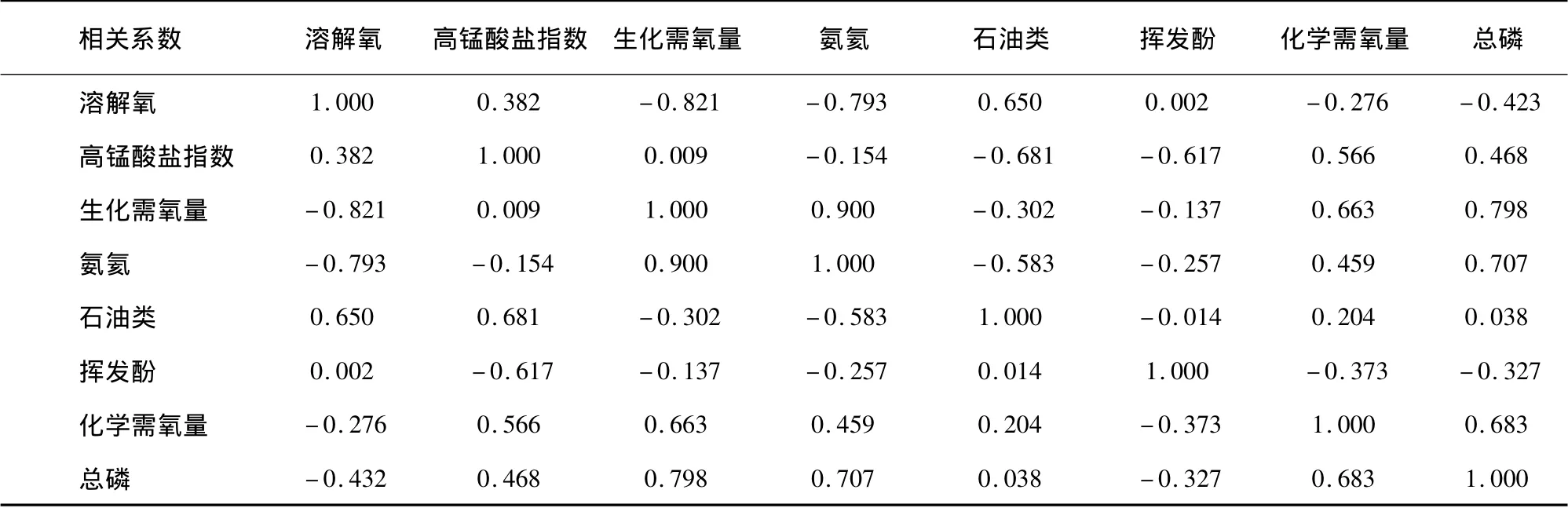
图10 相关系数矩阵

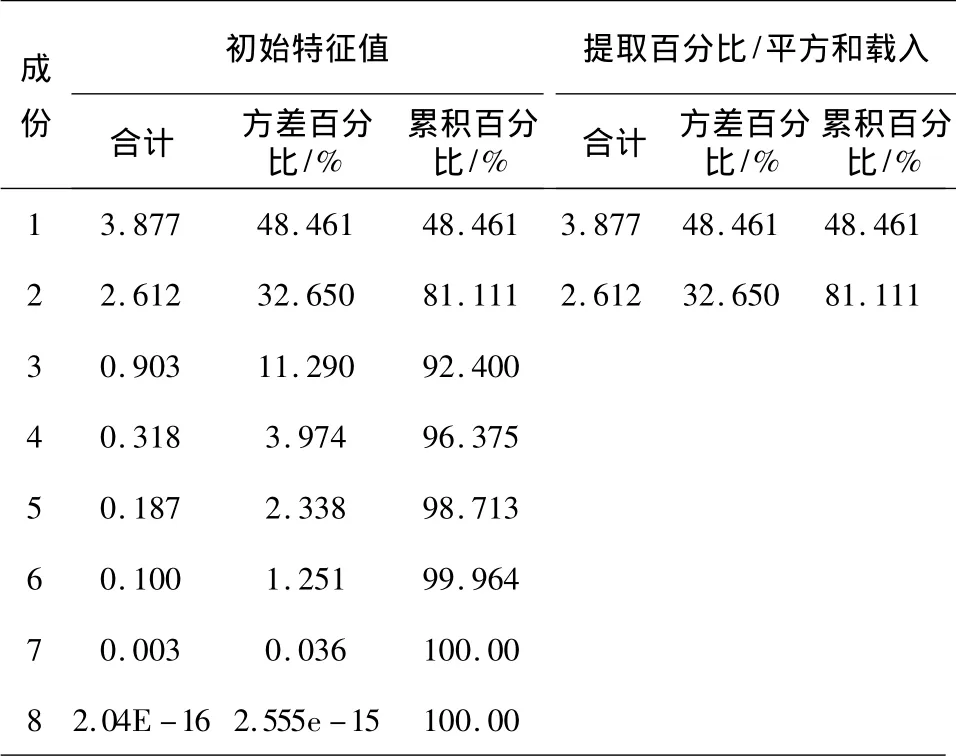
图11 主成分方差与方差贡献

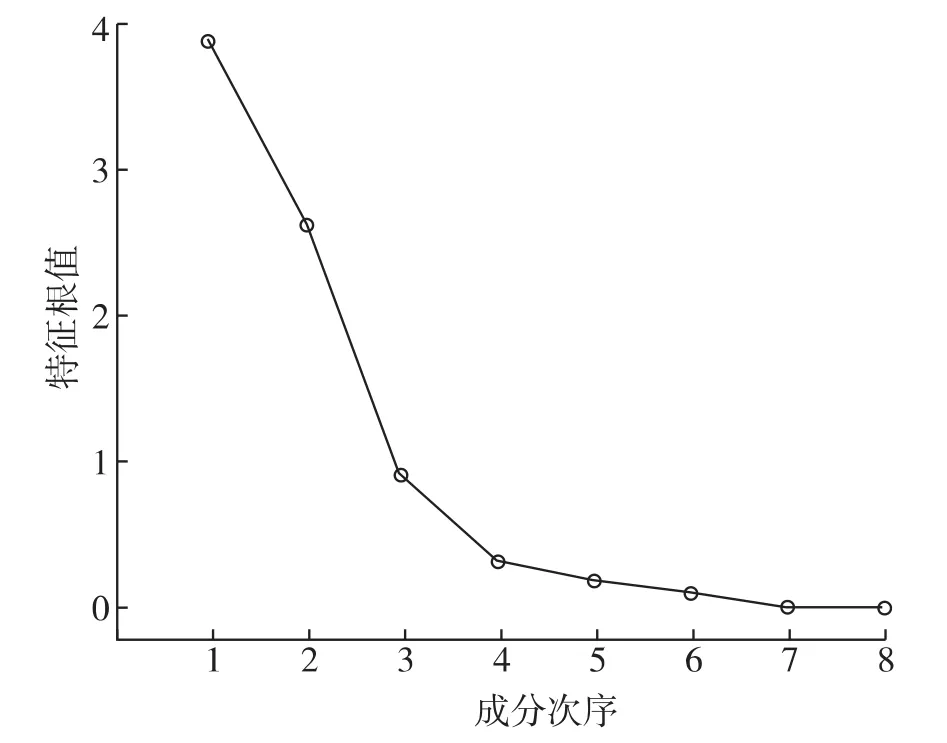
图12 特征根数值衰减折线

从初始因子荷载矩阵(图13)可知，生化需要量、氨氮、总磷在第一主成分上有较高载荷，说明第一主成分基本反映了这些指标的信息，高锰酸盐指数和石油类指标在第二主成分上有较高载荷，第二主成分主要反映的是这两个指标的信息。

初始因子荷载矩阵由SPSS直接得到，而主成分荷载矩阵(表3)需用初始因子荷载矩阵中数据除以主成分相对应特征值的平方根，得到2个主成分中每个指标对应的系数，才得到相应的主成分荷载值。

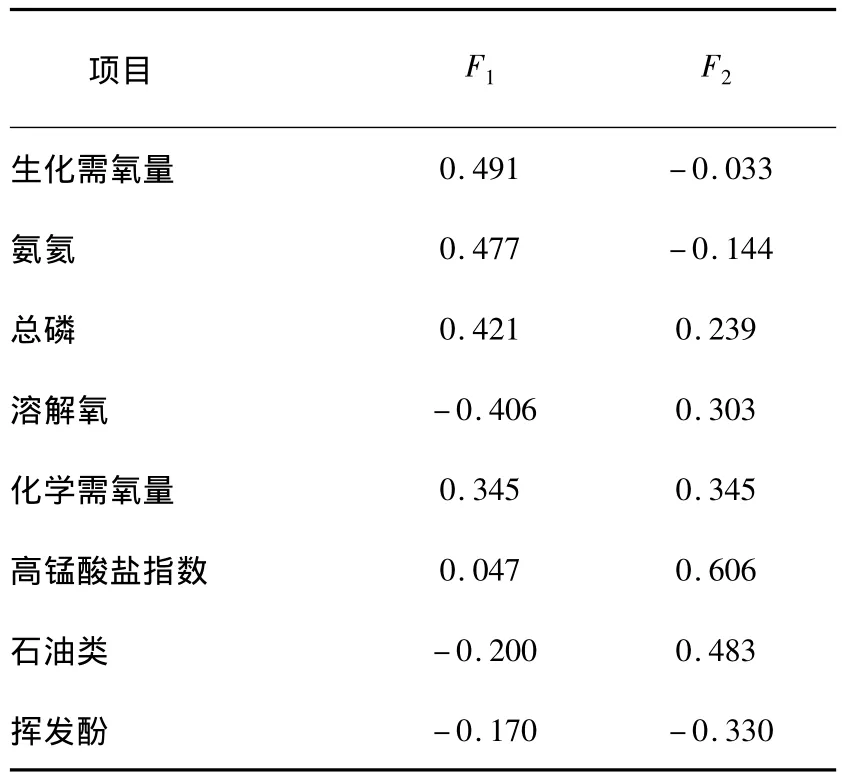
表3 主成分载荷矩阵

根据以上分析结果，得知:

F1为第一主成分，代表生化需要量、氨氮、总磷三个评价指标;F2为第二主成分，代表了高锰酸盐指数和石油类两个评价指标。

根据 λ1=3.877 ，λ2=2.612，得到相应的主成分表达式(综合评价函数)如下:

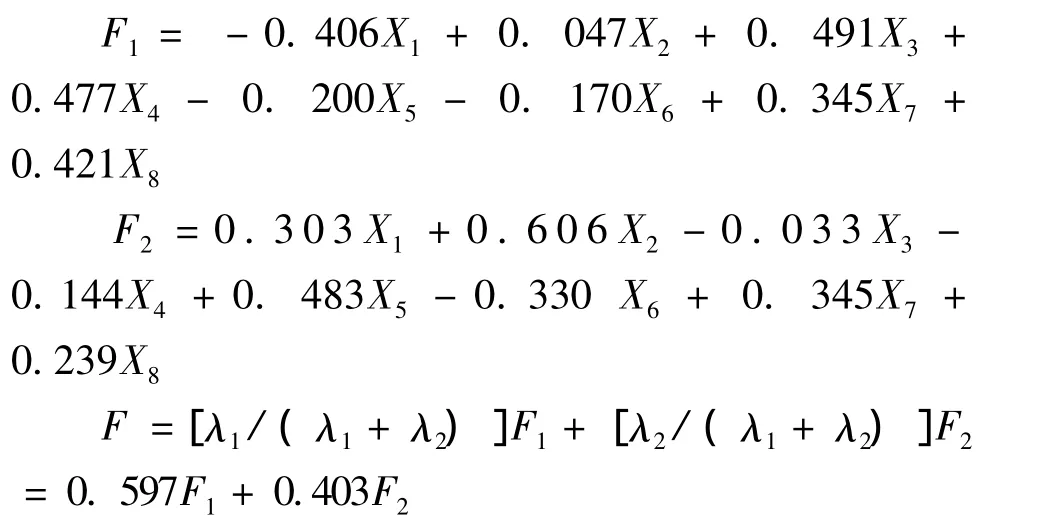
根据综合评价函数，计算各监测断面和整条河流的水质污染综合得分，计算结果见表4，给出水质污染程度的定量化描述，得分越大，表明污染越严重。

由表4可以看出，2011年串场河的水质污染程度排序为:

黄海大桥＞新兴公路桥＞沟墩大桥＞啤酒厂＞李舍＞廉贻大桥＞白驹镇北

从第一主成分F1得分的排名来看，黄海大桥得分远高于其他监测断面，说明该处生化需氧量、氨氮和总磷含量相对较高;从第二主成分F2得分排名来看，沟墩大桥和啤酒厂得分较高，说明此两处高锰酸盐指数和石油类污染较重。从水质监测数据来看，证实主成分分析结果较真实地反映了实际情况。

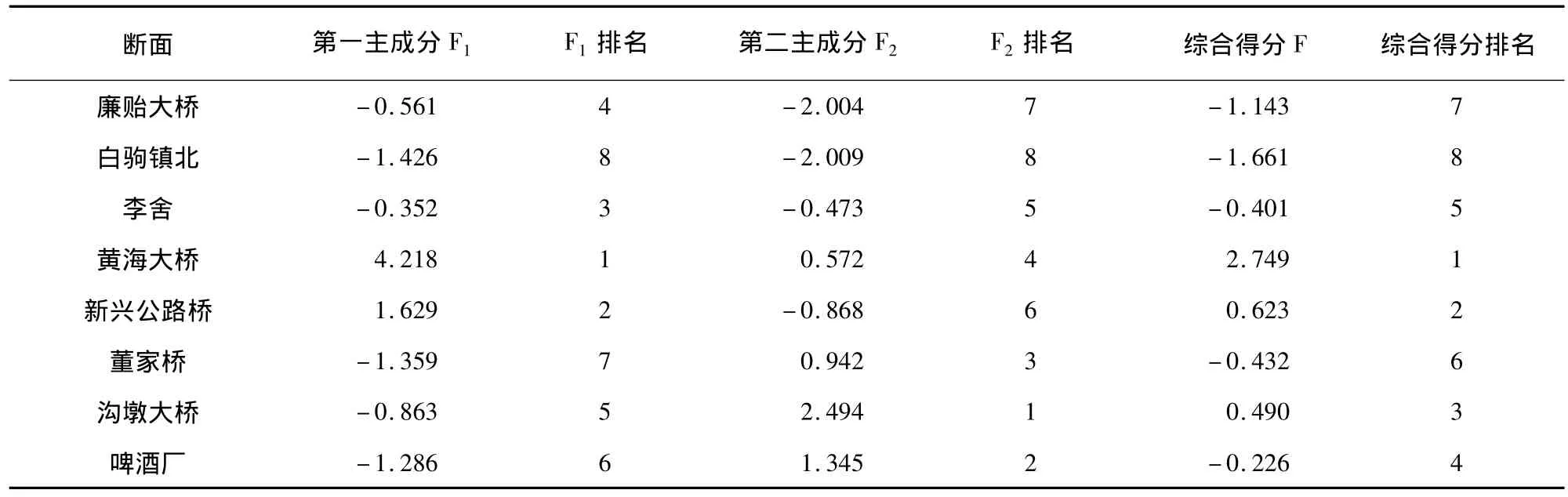
表4 各监测断面水质综合评价结果

4 结论

借助SPSS软件，采用主成分分析法研究串场河水质特征，结果表明:从原始水质数据中提取占总方差的81.111%的2个因子来反映水体的污染程度，经过分析识别得到串场河的2个主成分因子:生化需氧量、氨氮和总磷;高锰酸盐指数和石油类。结果与实际情况相吻合，说明主成分分析法是一种有效的水质评价方法。同时，在水质综合评价时，可以根据主成分分析法得出的结论，重点考虑排名靠前的指标，删除那些次要的指标，确定造成污染的主要成分。这样不仅避免了人为选择指标的随意性，更节省了监测所需的人力物力，使评价方法更加科学与准确。

[1]庞鸿宾.节水农业工程技术[M].郑州:河南科学技术出版社，2000:40－63.

[2]Huang B R，Fry J D.Root anatomical physiological and Morphological responses to drought stress for fescue cultivars[J].Crop Sci，1998(38):1017 － 1022.

[3]王艾，冯绍元，郑艳.主成分分析法在温榆河水质评价中的初步应用[J].北京水务，2011，(2):49－52.

[4]鲁斐，李磊.主成分分析法在辽河水质评价中的应用[J].水利科技与经济，2009，12(10):660 －662.

[5]方红卫，孙世群，朱雨龙，等.主成分分析法在水质评价中的应用及分析[J].环境科学与管理，2009，34(12):152－154.