遵义市环境空气质量预报详解

丁培林，张光红，曾 昶，朱 晶，张 坤

(遵义市环境保护监测中心站， 贵州 遵义 563000)

根据环境空气质量标准[1]，目前评价环境空气质量指标的参数主要是可吸入颗粒物(PM10)、二氧化硫(SO2)、二氧化氮(NO2)。空气质量预报也就是对未来某一区域内此3项污染物浓度值的预测，它以区域内环境空气质量现状监测和未来该区域内污染物排放预测为基础。环境空气质量预报有多种方法，限于条件，监测站系统一般采用历史数据回归法，通常认为未来时段的污染物浓度与气象因子有关，基本忽略了地形条件、源强变化等对污染物分布的影响[2－3]。遵义市确定采集的气象因子是风速、气温、温差(今日气温与昨日气温之差)、气压、压差(今日大气压与昨日大气压之差)、湿度6项，这与我站气象系统提供的参数相吻合。

1 回归概述

回归的过程是把污染物浓度当作因变量，各气象因子当作自变量，所要参与回归计算的历史数据(样本)在统计学上叫作“序列”，可以简单地理解为在实验室内作标线时所要准备的浓度点。这实际上是一个因变量对多个自变量的多元回归形式，并假设它们是多元线性的[4－5]。关于“序列”，我们的经验是样本量不宜取太多，在保证统计精度和计算速度的前提下，我们选取了最近三十天的历史数据，并随着日期延续不断更新，例如，今天(8月30日)选取的“序列”是8月1日至8月30日三十天的历史数据，明天(8月31日)选取的序列将是8月2日至8月31日的历史数据。编制预报的多元回归“序列”是预报的前提。

在光盘“预报详解”目录下所附的“序列示例”表就是我们所作一个“序列”情况，这个表实际上是为后续统计计算而设计，稍后会详细介绍。“序列”做完后，剩下的就是计算，即根据“序列”分别求出各污染物浓度对气象因子的多元回归方程。比较理想的状况是，通过气象台得到未来一天的气象因子变化情况，并能修正为监测点位的气象因子变化，然后将预报气象因子数值代入多元线性回归方程，得到不同监测点位不同污染物的预报浓度[6]。

由于多元回归方程的推演计算非常繁琐，单靠手工操作效率很低。目前，有很多的计算机程序可供利用和选择，能够大大地提高工作效率和水平。遵义市采用的统计程序是第四军医大学开发的DPS2000数据处理系统，该数据处理系统界面友好，功能强大。

2 案例分析

以下将详述遵义市环境空气质量预报的整个过程。

2.1 编制今日预报序列

“序列示例”表中列有十三个字段，分别为:ws(风速)、humid(湿度)、temp(气温)、press(气压)、温差、压差、SO21、NO21、PM1、SO22、NO22、PM2、date(监测日期)，其中SO21指第一个点位SO2监测值，SO22指第二个点位SO2监测值，以此类推，PM代表PM10。

每日中午收取各子站数据(遵义市的环境监测统计日为昨日12:00至今日12:00)，在序列表中新增当日记录，同时删除最上方的一条旧记录，始终保持30条记录，存盘退出，今日预报序列表便制作完成。

2.2 采用逐步回归法计算各污染物浓度对多元气象因子的回归方程

“序列示例.xls”为今日制作完成的预报序列表(图1)，首先打开DPS2000数据处理系统(图示为DPS3.01专业版)，然后选取多元回归计算数据区，在执行操作之前选中操作区，DPS2000数据处理系统自动将选中的数据区最右边一列视为因变量区，其余各列视为自变量区。数据区圈选时不包括第一行字段名。以下操作以计算SO21与各气象因子之间的回归方程为例，点击 A2单元格，然后按住“shift”键，利用垂直滚动条再点击G31单元格，这样便选中了第一个回归方程的计算区。

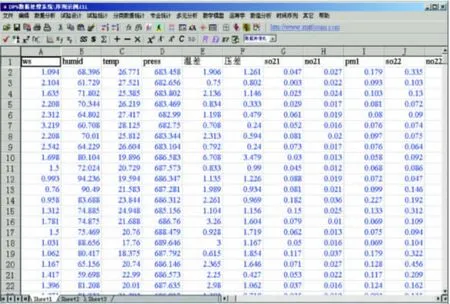
图1 序列示例

点击菜单栏的“多元分析”下的“回归分析”，选择“逐步回归”，弹出“confirm”对话框，要求引入尚未引入的回归方程的变量，点击“yes”，变量被不断地引入，直至“confirm”对话框中“尚未进入回归方程的变量及F值”一栏下不再发生变化，同时“当前方程”一栏下“上次R调整=×”值亦不再发生变化，点击“OK”。至此多元回归的各种统计量将在数据区后全部被计算出来(图2)。

图2 统计量计算

向下拉动垂直滚动条，找到并复制SO21对气象因子的多元回归方程，新建一个文本文件，取名为DPS2000.txt，将得到的多元回归方程粘贴上去(图3)。重新回到原始数据区，选中G列，点击“擦除”快捷按钮，删除G列数据(图4)。选中H列，将其拖曳至原SO21所在的G列，按照此前操作方式选中A 2∶G31数据区，计算出NO21与各气象因子的多元回归方程。

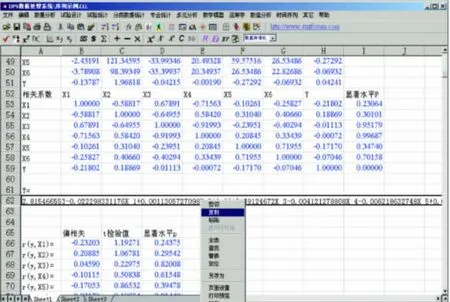
图3 获得SO21多元回归方程

图4 删除SO21数列

重复以上工作，不断将G列更新为其他污染物监测值所在列，完成A2∶G31之间数据区圈选，逐步回归出各污染物与各气象因子的多元回归方程，并将方程式粘贴到DPS2000.txt文件中(图5)。

图5 各污染物与各气象因子的多元回归方程

为便于DPS2000.txt准确导入预报模板，还应对该文件按统一数据位格式进行规范，即将常数项和系数项手工规范为统一长度(遵义市是保留7位有效数字)，常数项前留一空格是保留符号位，规定缺失的自变量系数为0，也应补回回归方程(图6)。

图6 补回缺失自变量系数

2.3 导入模板，完成预测浓度计算

遵义市在计算预测浓度时编制了一个excel模板，模板内容及各表之间的相互关系见光盘“预报详解”目录下的“预测模板.xls”文件(图7)。

首先，手工填写参与计算的气象资料(下图中黑框部分)，今日(9月26日)资料可从有气象设备的子站处获得，明日(9月27日)气象资料可通过气象台获得，必要时对气象台的预报资料参考预报站点的地理位置作一些修正。

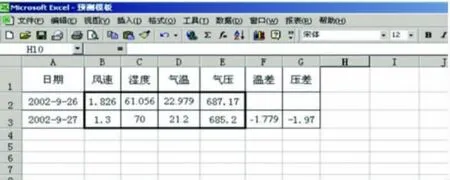
图7 预测模板

然后切换到回归方程表，点击菜单栏上“数据”下的“获取外部数据”，选择“导入文本文件”，找到DPS2000.txt文件，点击“导入”按钮，弹出文本导入向导对话框(图8);单击“下一步”，重新编排回归方程序列的分布线，分别将常数项定为一列，带符号的系数项定为一列，自变量项定为一列，单击“下一步”(图9)。最后单击“完成”，将回归方程导入到现有数据表的A1单元格中(图10)。

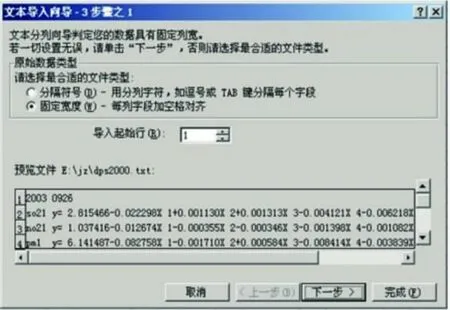
图8 文本导入向导——第一步

图9 文本导入向导——第二步

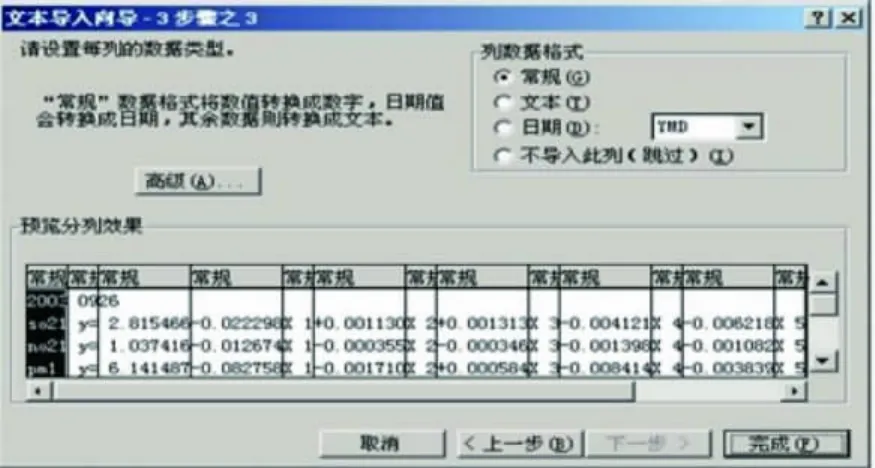
图10 文本导入向导——第三步

回归方程导入后，预算结果将在“预报成果”表中自动算出(图11)。

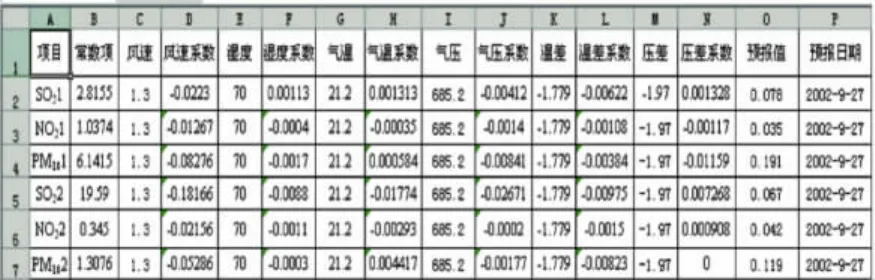
图11 预报成果

3 结论

采用逐步回归法建立的空气质量预报方法，在城市空气污染物排放源源强及其时空分布无太大变化的情况下取得了较好的预报效果。空气质量的预报方程都通过了效果检验，结果较为满意(表1)。

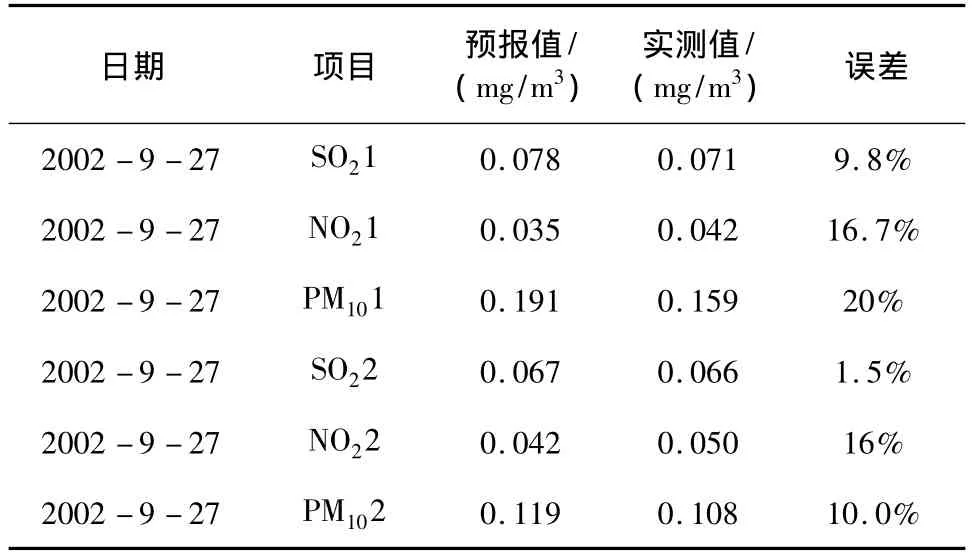
表1 预报值与实测值对比结果

以上介绍了遵义市环境空气质量预报数据的制作方法，当然仍有许多不完善和需要改进的地方，特别是手工向模板导入回归方程的步骤还比较繁琐，相信以后会有更好的解决方案。

[1]国家环保部.环境空气质量标准(GB 3095—1996)[S].北京:中国环境科学出版社，1996.

[2]国家环保部.环境影响评价技术导则(HJ/T 2.2—2008)[S].北京:中国环境科学出版社，2009.

[3]李本纲.北京市城区主要交通干线的噪声测量与分析[J].城市环境与城市生态，2000，13(2):11 －13.

[4]吴伟，李叶飞.回归分析法在工程项目利润预测中的应用[J].合肥工业大学学报:自然科学版，1999(S1):102－106.

[5]郑晓雨，贺仁睦，马进.逐步多元回归法在负荷模型扩展中的应用[J].中国电机工程学报，2011，31(4):72－77.

[6]熊德琪，陈守煜.城市大气污染物浓度预测模糊识别理论与模型[J].环境科学学报，1993，13(4):482－490.