一种基于RAMP算法的OFDM稀疏信道估计方法
丁敬校,王可人,金 虎,陈小波
(解放军电子工程学院,合肥230037)
1 引 言
正交频分复用技术(OFDM)由于具有频谱利用率高、抗频率选择性衰落强等优点,在现代无线通信领域得到了广泛的应用[1],如数字音频广播(DAB)、数字视频广播(DVB),以及无线局域网技术标准IEEE 802.11a和宽带无线接入技术标准802.16等。在OFDM系统中,为实现相干解调,需要在接收端获得信道状态信息,因此,对信道参数进行估计具有重要意义。
无线多径信道呈现稀疏特性,信道冲激响应的绝大多数能量只集中在少数几个多径分量上。传统的信道估计方法没有充分利用信道内在稀疏性这一先验知识[2],近年来有大量研究者对这一问题进行研究。文献[3]提出了一种基于修正最小二乘准则的稀疏信道估计方法,该方法需要先用GAIC(Generalized Akaike Information Criterion)准则估计出信道长度进而估计重要抽头的位置,在大信噪比时性能较好,但在信噪比低于某个值后,算法性能严重恶化。文献[4]提出一种基于近似 l0范数的信道估计算法,应用梯度下降法和梯度投影算法获得代价函数的最优解,从而得到信道的最稀疏解,但算法的复杂度较高。匹配追踪算法(Matching Pursuit,MP)作为一种高效的稀疏信号重构算法具有收敛速度快、易于实现等优点,在稀疏信道估计中得到广泛应用[5-7]。文献[6]提出了一种基于匹配追踪的信道估计,可在导频数量较少时保持有良好的估计性能。文献[7]在文献[6]的基础上进一步结合压缩感知理论采用正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法对OFDM时域信道冲激响应进行估计。但是这些方法均需要信道冲激响应的稀疏度作先验条件,而这在实际应用中是很难甚至根本无法获得的。
针对文献[6]和文献[7]中存在的问题,本文提出一种基于正则化自适应匹配追踪的稀疏信道估计算法,不需要信道冲激响应的稀疏度作先验知识,且算法的收敛速度快,估计效果好。
2 压缩感知
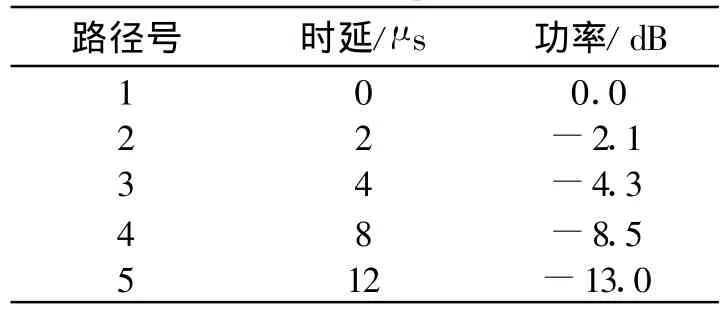
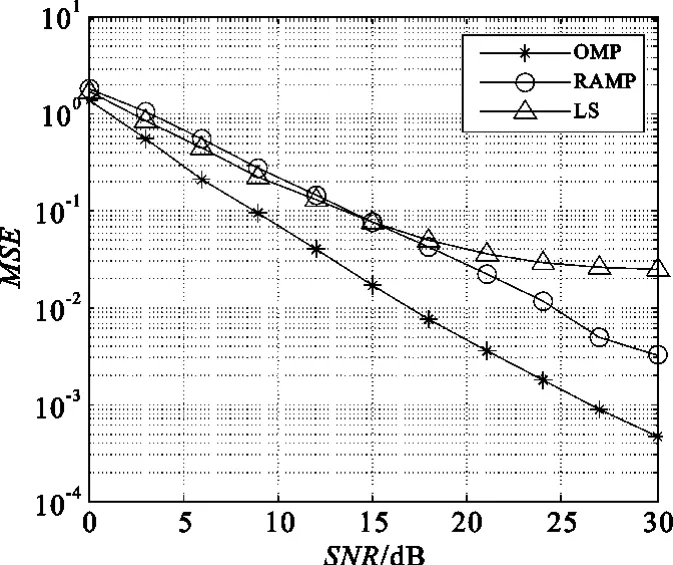
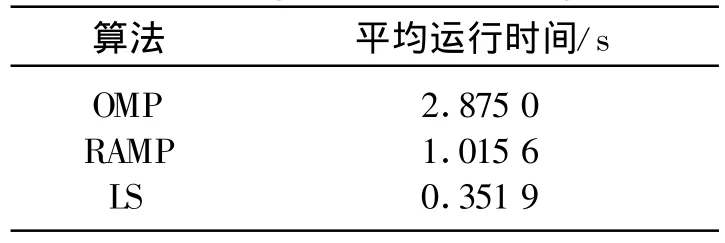
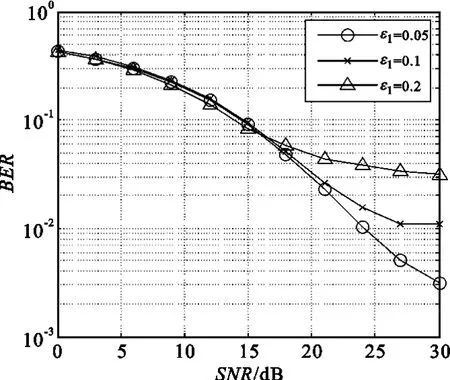
压缩感知是一种在已知信号稀疏或可压缩的情况下获取或重构信号的技术,它针对观察信号的一组线性测量值,通过重构算法恢复出稀疏信号[8]。对信号x∈RN,如果x中只有K个(K< 式中,e为噪声。若M≥K·lgN,且观测矩阵 Υ满足一定条件,则可以通过寻找式(1)的最稀疏解恢复信号x。目前恢复算法的思想主要有凸优化和贪婪迭代两种。 基于凸优化的思路主要是通过增加约束来取得最稀疏解,常用的是范数约束: 在此基础上出现了一系列算法,这些算法可以取得较好的恢复效果,但计算复杂度较高。 基于贪婪迭代的思路主要根据匹配追踪(MP)思想,通过局部最优化依次寻找各个非零系数。在此基础上发展了正交匹配追踪(OMP)及其改进算法分段匹配追踪(StMP)、子空间追踪(SP)等。Needell等人将正则化过程引入OMP算法中,提出正则化匹配追踪(ROMP)。该算法首先根据度量挑选出多个原子作为候选集,然后利用正则化实现对支撑集的二次筛选,快速、有效地重构出原信号。但是这些算法都是建立在稀疏度K已知的基础上。然而这在实际应用中往往是未知的,由此出现了不需要稀疏度K作先验知识的盲恢复算法——自适应匹配追踪(SAMP)[9],它通过设置一个可变步长,对信号的稀疏度进行估计,重构效果较好。文献[10]结合了ROMP和SAMP算法的优点,提出了用于稀疏度未知时进行盲恢复的正则化自适应匹配追踪算法(RAMP),效果较好。 式中,L为路径数,τk为第k条路径上的延时,αk为第k条路径的衰落。若信道的相干时间远大于OFDM的符号周期,则可以认为在一个OFDM符号内,信道的冲激响应是不变的。以OFDM系统的采样周期对h(t)进行采样,信道的稀疏性体现在h(t)的采样信号中非零元素的个数远小于采样信号的长度。 在图1所示的OFDM系统中,在发送端,数据经过串并转换后,将导频序列插入数据并进行IFFT变换,加上循环前缀并送至中频,发送数据经过多径时变信道后到达接收端。设多径衰落信道由L条路径组成,则信道响应如式(3)所示: 图1 OFDM系统框图Fig.1 The block diagram of OFDM system 在接收端,去掉数据中的循环前缀,提取导频,并进行信道估计。经过FFT变换之后的信号可以表示为 式中,Y是接收到的频域信号;X=diag(X(0),X(1),…,X(N-1)),X(i)表示一个OFDM内第 i个子载波上的数据;H是频域信道矩阵;n是N×1维的复加性高斯白噪声。 设系统采用梳状导频结构,有 P路导频子载波,S为P×N的选择矩阵,用于从N个子载波中选出与导频对应的P行,则接收到的导频位置的信号可以表示为[7] 其中,YP=SY,XP=SXST,WP=SW,nP=Sn,W是DFT变换矩阵。 在式(5)中,令 y=YP,Υ=XPWP,x=h,e=nP,则可以将对信道 h的估计转化为如式(1)所示的稀疏信号重构问题,通过一定的重构算法即可恢复h。 对于式(5),考虑到导频数量大于路径数,即P≥L,可以得到最小二乘估计为 文献[7]利用信道的稀疏性,提出一种基于正交匹配追踪的OFDM信道估计算法,其目标是直接估计出h中非零元素的位置和大小,基本思路是:在第j次 迭 代过 程 中,确 定索 引 λj,使 得取得最大值,其中 φλ表示 Υ的第λj列,并增大索引集;同时利用最小二乘法估计得到一个新值使arg min‖y-ΥΛjh‖ ,更新残差 :yj=ΥΛj·hjλj,rj=y-yj。经过K次迭代,OMP算法就可以输出K稀疏的向量 h。 从上述过程可以看出,OMP算法需要已知信号的稀疏度才能实现精确重构,对稀疏度的过大或过小估计都会造成算法性能下降。虽然可以通过设置一个阈值替代稀疏度作为迭代的终止条件,但此时算法的收敛性可能无法得到保证。 正则化自适应匹配追踪算法[10]采用阶段转换的方式逐步增加候选集中原子的个数,将同一个迭代过程分为多个阶段,用可变步长而不是稀疏度作为每次选择的原子数目,通过步长的不断增大逐步逼近稀疏度K,从而实现了在稀疏度未知时的信号精确重建。算法的具体步骤如下: (1)初始化:迭代次数 t=1,残差r0=y,初始步长 s=s0≠0,阶段 stage=1,索引集 Λ=,候选集J=; (3)计算相关系数: 并从中找出s个最大值对应的索引存入候选集J中; (4)通过正则化将候选集 J中的原子进行分组,选出能量最大的一组J0J,其中原子的相关系数满足 (5)更新支撑集 ΥΛ,Λ=Λ∪J0; 其中,ε1、ε2分别是迭代终止和阶段转换阈值,应根据具体信息适当设置大小。通过这两个阈值的设置,算法可以自动调整当前步长,判断是否进入下一阶段或者下一次迭代,因此不需要将稀疏度作为先验知识,同时也避免了算法无法收敛或者过匹配现象的出现。步骤4中的正则化过程可以保证每次入选的原子都是候选集中能量最大的一组,且最多经过K次迭代就可以得到用于信号精确重建的支撑集。这既能使算法获得较好的重建质量,又可以缩短算法的运行时间。 (7)如果 为了验证RAMP算法的性能,本文进行了如下仿真。在16QAM-OFDM系统中,子载波个数N=512,循环前缀长度CP=16,共有32路子载波用来传输导频符号。信道为瑞利多径衰落信道,采用Jakes模型,功率延迟谱服从负指数分布,参数如表1所示。 表1 信道参数Table 1 Channel parameters 均方误差按式(7)计算: 图2和图3分别比较了不同算法BER和MSE性能。图2中给出了信道状态已知时的BER曲线作为参考。仿真时,LS算法的导频均匀放置,OMP与RAMP算法的导频随机放置。阈值 ε1设置为0.05*‖r‖2,ε2设置为 0.3*‖r‖2,其中‖r‖2表示r的2范数。可以看出,在低信噪比情况下,RAMP算法的性能稍差,随着信噪比的增加,3种算法的性能均逐渐提高;在大信噪比时,RAMP算法与OMP算法均优于LS估计的性能,且这种优势随着信噪比的增加变得更加明显。 图2 不同算法的BER性能曲线Fig.2 Comparison of BER performance between different algorithms 图3 不同算法的MSE性能曲线Fig.3 Comparison ofMSE performance between different algorithms 表2给出了各种算法的平均运行时间。由表可知,此时RAMP算法的运算时间小于OMP算法,大于LS算法,这与算法的误码率性能是一致的。考虑到与OMP算法相比,由于RAMP算法不需要信道冲激响应的稀疏度作先验条件,因此,该算法的实用性更高。 表2 算法运行时间对比Table 2 Running time of different algorithms 图4所示为阈值ε1对误码率性能的影响。可以发现,在低信噪比情况下,算法的性能并没有随着ε1的减小而提升,而是在信噪比大于某一个值时,算法的性能随着 ε1的降低逐步改善。可以通过降低阈值ε1进一步提高大信噪比情况下RAMP算法的性能,但算法的运行时间也会相应增加,需要在算法的恢复性能和计算时间上进行折衷。 图4 阈值 ε1的变化对误码率曲线的影响Fig.4 The effect of ε1on BER curve 本文提出了一种基于RAMP的OFDM系统稀疏信道估计方法,该方法避免了现有算法需要信道稀疏度作先验条件的不足,可在信道稀疏度未知的情况下准确估计出信道的冲激响应。仿真结果表明,该方法收敛速度快,估计效果好,具有可应用性。但是,阈值的选取对算法的性能影响较大,如何根据有关信息确定最佳的阈值还需要进一步研究。 [1]龚钢,雷维嘉,谢显中.基于梳状导频分布的OFD M信道估计改进方法[J].电讯技术,2011,51(4):102-105.GONG Gang,LEI Wei-jia,XIE Xian-zhong.An improved channel estimation algorithm based on comb-type pilot in OFDM systems[J].Telecommunication Engineering,2011,51(4):102-105.(in Chinese) [2]Bajwa W U,Haupt J,Sayeed A M,et al.Compressed channel sensing:A new approach to estimating sparse multipath channels[J].Proceedings of the IEEE,2010,98(6):1058-1077. [3]Raghavendra M R,Giridhar K.Improving channel estimation in OFDM systems for sparse multipath channels[J].IEEE Signal Processing Letters,2005,12(1):52-55. [4]陈书贞,张亚静,练秋生.OFD M系统中基于压缩传感理论的信道估计算法[J].信号处理,2010,26(1):157-160.CHEN Shu-zhen,ZHANG Ya-jing,LIAN Qiu-sheng.Channel estimation algorithm based on compressed sensing for OFDM systems[J].Signal Processing,2010,26(1):157-160.(in Chinese) [5]Cotter S F,Rao B D.Sparse channel estimation via matching pursuit with application to equalization[J].IEEE Transactions on Communications,2002,50(3):374-377. [6]朱行涛,刘郁林,徐舜,等.一种基于匹配追踪的OFDM 稀疏信道估计算法[J].微波学报,2008,24(2):73-76.ZHU Xing-tao,LIU Yu-lin,XU Shun,et al.An OFD M sparse channel estimation algorithm based on matching pursuit[J].Journal of Microwaves,2008,24(2):73-76.(in Chinese) [7]何雪云,宋荣方,周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究[J].南京邮电大学学报(自然科学版),2010,30(2):60-65.HE Xue-yun,SONG Rong-fang,ZHOU Ke-qin.Study of compressive sensing based sparse channel estimation in OFDM systems[J].Journal ofUniversity of Posts and Telecommunications(Natural Science Edition),2010,30(2):60-65.(in Chinese) [8]张先玉,刘郁林,王开.超宽带通信压缩感知信道估计与信号检测方法[J].西安交通大学学报,2010,44(2):88-92.ZHANG Xian-yu,LIU Yu-lin,WANG Kai.Ultra wideband channel estimation and signal detection through compressed sensing[J].Journal of Xi′an Jiaotong University,2010,44(2):88-92.(in Chinese) [9]Do T T,Gan L,Nguye N,et al.Sparsity adaptive matching pursuit algorithm practical compressed sensing[C]//Proceedings of Asilomar Conference on Signals,System,and Computers.Pacific Grove,California:IEEE,2008:581-587. [10]刘亚新,赵瑞珍,胡绍海,等.用于压缩感知信号重建的正则化自适应匹配追踪算法[J].电子与信息学报,2010,32(11):2713-2717.LIU Ya-xin,ZHAO Rui-zhen,HU Shao-hai,et al.Regularized adaptive matching pursuit algorithm for signal reconstruction based on compressive sensing[J].Journal of Electronics and Information Technology,2010,32(11):2713-2717.(in Chinese)

3 系统模型



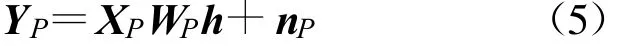
4 信道估计
4.1 最小二乘估计(LS)
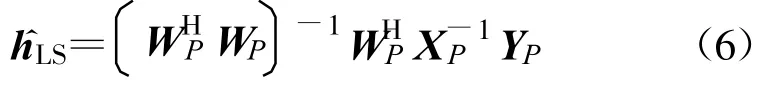
4.2 基于正交匹配追踪(OMP)的信道估计算法
4.3 基于正则化自适应匹配追踪(RAMP)的信道估计算法

5 仿真分析
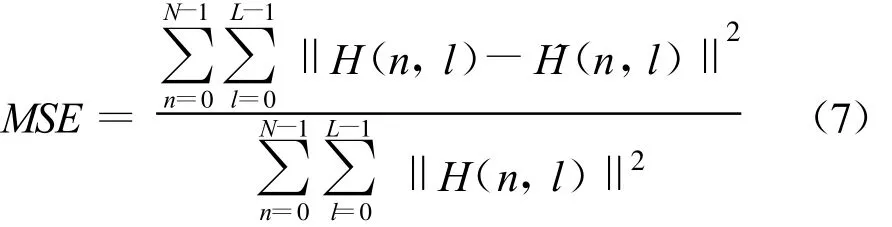

6 结束语

