基于三角网格模型的剖面轮廓信息提取

张小青，吴坤华，黄 鹤

(1.福建水利电力职业技术学院水利工程系，福建永安366000;2.福建水利电力职业技术学院电气工程系，福建永安366000;3.北京建筑工程学院测绘与城市空间信息学院，北京100044;4.现代城市测绘国家测绘地理信息局重点实验室，北京100044)

基于三角网格模型的剖面轮廓信息提取

张小青1，吴坤华2，黄 鹤3，4

(1.福建水利电力职业技术学院水利工程系，福建永安366000;2.福建水利电力职业技术学院电气工程系，福建永安366000;3.北京建筑工程学院测绘与城市空间信息学院，北京100044;4.现代城市测绘国家测绘地理信息局重点实验室，北京100044)

为获得三角网格模型的剖面轮廓信息，提出分层切片和邻接排序算法。首先将模型中的三角形面片在剖切方向上分组;然后计算每一组三角形和剖切平面的交线，并按邻接顺序将交线按首尾顺序连接;最后对每一层非封闭的轮廓线进行封闭处理，并计算剖面面积。试验结果表明，该算法高效简单，能够有效地获得封闭的剖面轮廓环。

三角网格模型;网格剖切;分层切片;邻接顺序;轮廓信息

一、引 言

三维模型中的三角网格模型具有许多良好的几何特性，它能够用多个面片逼近复杂形体的表面，而且容易处理，因此三角网格模型被广泛应用于计算机图形学、机械仿真、科学计算可视化等领域［1］。剖面轮廓线是三维模型的一个重要特征，它代表模型在某一位置处的大致轮廓和几何形状，并体现三维模型的基本外观。如在文物三维展示和虚拟修复中，往往需要观察其各个部位的截面特征，为达到既不损坏文物、又能够观察文物的截面形状和大小的目的，可采用对三维模型进行剖切处理的方法实现文物剖面轮廓信息的提取。

目前常用的剖面轮廓线提取算法主要分两类［2-4］：一类是先建立网格模型中的顶点、边和三角面片的邻接拓扑关系，再计算网格模型与剖切平面的交点，此类算法的优点是交点是有序的，但建立网格模型的完整的相邻拓扑关系比较费时;另一类算法是根据网格模型中三角形的几何特征，预先将三角形按特定法则进行排序和分组，并在每组中建立模型的点、边和三角形面片的邻接拓扑关系，再用平面对组中的三角形进行剖切处理。后一类算法只需比较每个小组中的三角形和剖切平面的位置关系，而在每个小组中建立网格模型中的顶点、边和三角形之间的相邻拓扑关系，减少了三角形面片和切割平面空间位置关系的判断次数，简化了网格模型拓扑关系的构建工作。

本文采用OBJ格式的三维模型数据，利用分层切片和邻接排序算法，获得了三角网格模型的剖面轮廓信息，并对其处理结果进行了分析。

二、轮廓线生成算法

本文的剖切算法可归纳为读取模型数据，即先提取模型中的三角形顶点信息，将三角形在剖切方向上分组;然后在每一组中，比较三角形和剖切平面的空间位置关系，如果三角形和剖切平面相交，则将交线添加到交线组合中;最后对交线排序并进行封闭处理，获得封闭的轮廓线。算法流程如图1所示。

图1 轮廓线生成算法流程

1.模型中的三角形面片分组

影响剖切算法效率的因素有两个［2-4］：一个是模型中三角形的数量;另一个是剖切层数。为了提高算法效率，将模型中的三角面片进行预处理，即将模型中的三角形按照一定规则分成多个小组。本文是沿着Z轴方向剖切，即将模型中的三角形面片按其顶点坐标Z值的大小进行排序，求出网格模型中的Z坐标最小值Zmin和最大值Zmax，模型中的每个三角形面片被剖切的顺序由该三角形的Z坐标最小值Zmin确定。假设剖切间距为d，Zi表示第i层剖切平面的高度，则第一层剖面的Z坐标为Z1，其值为模型中Z坐标最小值Zmin与剖切间距为d之和，第i层剖面高度的Z坐标为Zi，第i+1层剖面的Z坐标为Zi+1，相邻剖面之间的计算公式为

Zi+1=Zi+d (1)

模型中三角形分组算法原理为：设Zi-1为第i-1层剖切平面的高度，Zi(i=1，2，…，n)为第i层剖切平面的高度，则存放在第i层剖切轮廓上的三角形面片由如下关系确定：当某个三角形的 Zmin和Zmax满足公式：Zi-1≤Zmin＜Zi，而且Zmax≥Zi，则该三角形被分在第i个小组。

2.判断三角形面片与剖切平面的位置关系

由于网格模型是由许多三角形构成的，因此模型与剖切平面的相交问题，可转化为模型中的三角形与剖切平面的相交问题。图2表示了网格模型与平面的相交情况，粗的多边形线段表示相交线，将这3条相交线段顺序连接，从而构成剖面轮廓多边形。

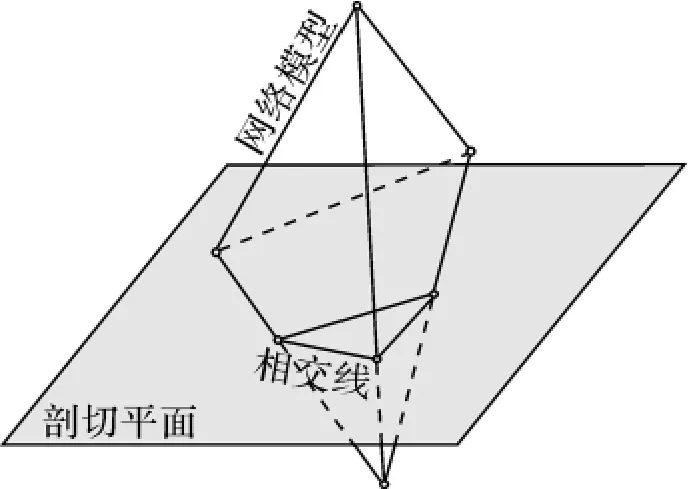
图2 平面剖切网格模型

模型中的三角形和剖切平面是否有交点，可以通过计算三角形的每个顶点与平面的有符号距离，通过3个顶点的有符号距离，对剖切平面和模型中的三角形的位置关系进行判断。三角形与剖切平面的空间位置关系，采用以下原则来进行判断［6］：假设剖切平面方程为ax+by+cz+d=0，模型中的三角形的顶点P(X，Y，Z)到平面的有向距离为D，其值可表示为

根据D值符号相同或不相同的情况，可确定三角形和平面的空间位置关系，包括5种情况，如图3所示，除了图3(a)中的三角形和平面没有交点，图3中(b)～(e)均存在交点。

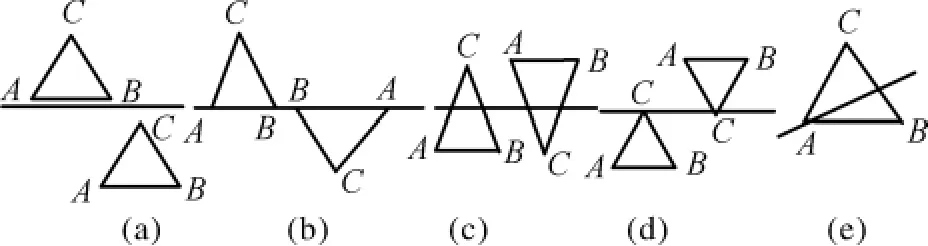
图3 三角形和平面的相交情况

3.轮廓线封闭处理

获得交线组合后，再对交线进行排序构建封闭轮廓环，先从交线组合中，任意取出一条交线，并将这条交线添加到一个新交线组合中，每条交线都有头节点和尾节点。从这条交线的尾节点开始，寻找下一条交线上离这个尾节点距离最近的点，称满足要求的交线为相关线。由于这些交线都是同一层剖面上的交线，所以它们具有相同的Z坐标，判断两点的距离公式为

式中，(xz，yz)是取出的第一条交线的尾节点坐标。如果找到的最近点是相关线的头节点，那么把这条交线添加到上述新交线组合中，并将这条相关线添加到前一条交线的后面;如果找到的最近点是相关线的尾节点，则将这相关线的头节点和尾节点顺序改变，同样将这条已更改头节点和尾节点顺序的交线添加到上述新交线组合中。继续上述算法，直至这层剖面的交线都添加到上述新交线组合中。

将交线排完顺序后，要检查每一组交线是否封闭。如果轮廓线不封闭［7］，则要进行封闭处理，在排完序的交线组合中，查找其尾节点是断开的(即有断点)某条交线，若找到这样的交线，称之为断开线。首先计算该断开线的断点与其他交线(如果有多条断开线)的断点之间的距离，并将这些距离值进行比较，找到最小距离的那条断线，这个最小距离值以D1表示，这条交线称为相关线;然后计算该断开线的终点与轮廓线中的起始线的起点之间的距离，令这个距离值为D2。轮廓线中的起始线是这样的一条交线，即轮廓线是以这条交线的尾节点开始，并以这条交线的头结点结束。如果距离值D1小于距离值D2，则在断开线的尾节点和相关线的头节点之间生成一条线;反之，则在断开线和轮廓线的起始线之间生成一条线，令生成的那条线为轮廓线的起始线。继续检查是否有断开线，若有，则继续上述算法。最终得到一条正确封闭的轮廓线，并检查轮廓线不相互交错以及不通过原来的线条。

4.剖面面积计算

将每一层剖面轮廓线进行首尾排序之后，形成完整封闭的轮廓环，每一层轮廓环可构成简单多边形，对于由顶点A1、A2、…、An构成的简单多边形，令顶点Ai的坐标为(xi，yi，zi)(i=0，1，…，n)，由于该剖切方向是沿着Z轴，每一层的轮廓线具有相同的Z坐标，其面积计算公式为［8］

三、试验结果与分析

本文采用的兔子网格模型如图4所示，本文算法是在VC#2008环境下，调用OpenGL函数库编程实现模型的显示，将网格模型沿坐标轴Z轴方向剖切了11层，获得每一层剖面轮廓线，进行排序构建首尾相连的轮廓线，并将未封闭的轮廓线进行封闭处理。如图5所示，提取的是第8层剖面轮廓线，轮廓线中间有断开，将其进行封闭处理之后，如图6所示。得到封闭的剖面轮廓线。剖面轮廓线能很好地表达模型的几何形状，图7为第8层剖面面积计算结果。

图4 兔子网格模型

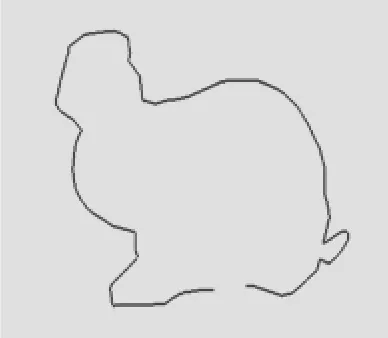
图5 轮廓线封闭前

图6 轮廓线封闭后

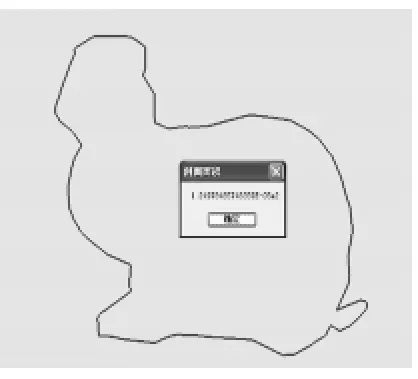
图7 剖面面积计算

四、结束语

本文提出的剖切算法能对一些复杂或有拓扑错误的模型有很好的适用性。由于将模型中的三角形在剖切方向上进行了分组，减少了遍历与剖切平面相交的三角形的次数，能够很好地提高算法效率。利用交线的首尾节点拓扑关系对交线进行排序，而不需要对模型建立复杂的拓扑邻接关系，利用最近距离法将轮廓线进行封闭处理，从而得到完整封闭的轮廓线。在计算机图形学、机械仿真和文物三维展示等领域，往往需要观察模型的内部或截面构造，这就需要通过剖切算法来提取剖面轮廓特征，轮廓线能够很好地表现三维模型的剖面特征，因此，剖切算法具有重要的应用价值。

［1］ 张瑞，骆岩林，周明全，等.文物数字化的关键技术［J］.北京师范大学学报：自然科学版，2007，43 (2)：150-153.

［2］ 王静亚，方亮，郝敬宾.STL模型特征面片自适应分层算法［J］.计算机应用研究，2011，28(6)：2361-2364.

［3］ 潘海鹏，周天瑞，朱根松，等.STL模型切片轮廓数据的生成算法研究［J］.中国机械工程，2007，18(17)：2076-2079.

［4］ 谢存禧，李仲阳，成晓阳.STL文件毗邻关系的建立与切片算法研究［J］.华南理工大学学报：自然科学版，2000，28(3)：33-38.

［5］ 张小青，朱光，侯妙乐，等.基于四面体的不规则表面文物体积计算［J］.测绘通报，2011(10)：50-52.

［6］ VATANI M，RAHIMI A R，BRAZANDEH F，et al.An Enhanced SlicingAlgorithm UsingNearestDistance Analysis for Layer Manufacturing［J］.World Academy of Science， Engineering and Technology， 2009，49：721-726.

［7］ TOPCU O，TASCIOGˇLU Y，ÜNVER H Ö.A Method for Slicing CAD Models in Binary STL Format∥6th International Advanced Technologies Symposium(IATS’11).Elazigˇ，Turkey：［s.n.］，2011.

［8］ 王泉德.任意三角网格模型体积的快速精确计算方法［J］.计算机工程与应用，2009，45(18)：32-34.

Extraction of Section Contour Information Based on Triangular Meshes

ZHANG Xiaoqing，WU Kunhua，HUANG He

0494-0911(2012)09-0026-03

P23

B

2012-04-25

张小青(1980—)，女，江西东乡人，硕士，助教，主要研究方向为精密工程测量。