栅格数据的等差分纬线多圆锥投影转换
叶远智
(浙江省地理信息中心,浙江杭州310012)
栅格数据的等差分纬线多圆锥投影转换
叶远智
(浙江省地理信息中心,浙江杭州310012)
等差分纬线多圆锥投影没有直接的投影转换公式,通过已有公式与部分参考坐标详细推导出正解转换公式,并计算规则经纬间隔控制点坐标。介绍在ArcGIS Desktop中使用控制点进行栅格纠正,实现栅格数据投影转换的方法,以及该方法在实际应用中的各项优势。
等差分纬线多圆锥投影;栅格转换;ArcGIS
一、引 言
等差分纬线多圆锥投影是任意多圆锥投影的一种,是我国制图工作者根据我国领土的形状和位置,并指定变形分布,于1963年设计的。该投影在我国编制各种比例尺世界政区图及其他类型世界地图中已得到较广泛的使用,并获得较好效果。该投影中纬线为对称于赤道的同轴圆圆弧,圆心位于中央经线上。中央经线为一直线,其他经线为对称于中央经线的曲线,且离中央经线越远,其经线间隔越成比例地递减;极点表示为圆弧,其长度为赤道投影长度的二分之一,经纬网的图形有球形感。
在制图时,选取东经150°为中央经线,可使我国被配置在地图中接近于中央经线的左侧,且我国面积相对于同一条纬带上其他国家的面积不会因面积变形而有所缩小,图形形状比较正确,图面图形完整,没有裂隙,也不出现重复,保持太平洋完整,可显示我国与邻近国家的水陆联系。由于该投影的性质是接近等面积的任意投影,因此我国绝大部分地区面积变形小。在日常使用的世界地图中,如气候类型和洋流图、世界政区图和自然带的分布图都是采用的这种投影图。
由于该投影没有提供直接的投影公式,因此在栅格数据进行投影变换时,首先需要进行公式拟合;再通过公式计算生成固定经纬网格的控制点;最后以控制点坐标为依据,采用纠正方法完成投影变换。
二、投影公式拟合

式中,a=0.9953537;b=0.014 761 38;R=6 371 116 m; φ以弧度计。
该投影的极坐标公式为

投影计算中央经线上x0、y0的公式为
式中,xn、yn是边缘经线上(Δλ=180°)的直角坐标值;b=1.1;C=0.000 505 050 5,计算直角坐标的方法如图1所示。

图1 投影后直角坐标计算示意图
由图1可知计算δn的公式如下

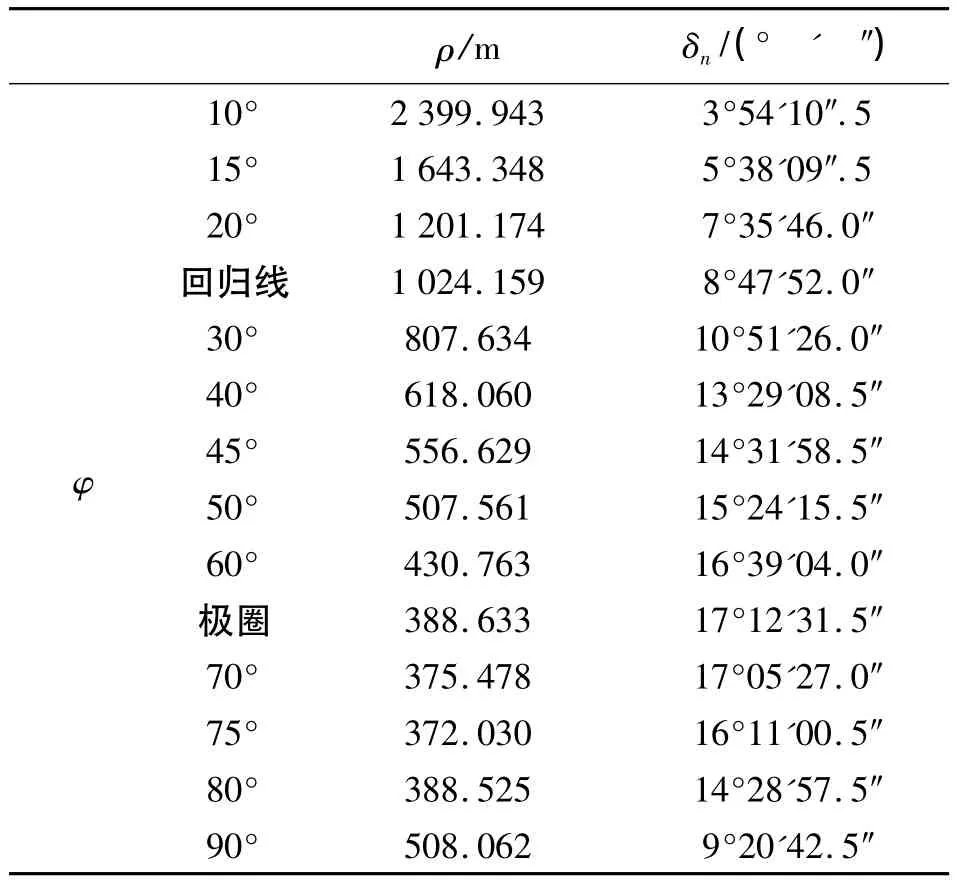
表1 纬圈半径ρ与极角δn参考值
表1中ρ为比例尺为1∶10 000 000时的纬圈半径长度,单位为cm。
根据计算直角坐标的公式

将表1经式(1)、式(4)计算可得到表2。

表2 各纬度x0、xn、yn参考值 m
由x坐标的图形分布情况,可确定x的拟合曲线应为奇次方程。综合考虑精度和计算量,实际采用一元五次多项式拟合,并选用1stOpt软件进行曲线拟合的参数估算求解,代码本如图2所示。拟合曲线与坐标点的套合情况如图3所示。
由y坐标的图形分布情况,可确定y的拟合曲线应为偶次方程,实际采用一元六次多项式拟合,代码本如图4所示。拟合曲线与坐标点的套合情况如图5所示。

图2 x坐标五次拟合代码本

图3 x坐标五次拟合曲线图

图4 y坐标六次拟合代码本

图5 y坐标六次拟合曲线图
依次先由式(1)求解(x0,y0),再由(x,y)坐标五次、六次拟合公式求解(xn,yn),然后由式(2)、式(3)计算ρ、δn、δi,最后按式(4)计算得到(xi,yi),即完成等差分纬线多圆锥投影的正解转换。
三、生成控制点
在所得到的投影公式的基础上,进行控制点的计算则比较简单。按照最后成图尺寸的需要,一般情况下1∶24 000 000比例尺的世界地图可采用5°间隔的控制点作为栅格纠正的依据;1∶10 000 000比例尺的地图可采用2.5°间隔的控制点;其他比例尺制图可酌情进行控制点加密或抽稀。
四、栅格纠正
在将地理坐标的栅格数据进行纠正前,应先对栅格数据进行平移,确保正确的中央经线位置。栅格纠正采用ArcGIS Desktop中的Georeferencing工具,该工具较其他软件使用上相对简单,纠正的效率也较好,并可方便与各类主流矢量数据进行叠加,方便后期制图需要。
在打开工具栏后(如图6所示),选择需进行纠正的栅格数据,并打开 Link Table工具。从 Link Table工具中可直接导入生成的控制点,其格式为经度、纬度、y直角坐标、x直角坐标,并以制表符进行间隔。导入控制点后务必选取转换方法为Adjust,如图7所示。

图6 Georeferencing工具栏

图7 Link Table工具界面
五、结束语
本文通过已有公式和部分参考坐标,借助曲线拟合软件推导出等差分纬线多圆锥投影的正解转换公式,较以往其他采用纸质图量算参考点坐标的方法,其计算方法更为严密,精度更为可靠。栅格数据采用纠正方法进行转换,较单像素逐点转换速度更快,避免了栅格数据在投影转换时的插值计算,转换方法简单。采用ArcGIS Desktop软件完成栅格数据纠正,相比其他栅格数据处理软件易用性更佳,在处理矢量数据方面,ArcGIS软件中可使用Spatial Adjustment工具利用控制点完成数据转换,实现同一种方法同时完成两类数据的投影转换。文中的方法已在多个项目中进行实际使用,并取得了理想的效果。
[1] 胡毓钜.地图投影图集[M].3版.北京:测绘出版社,2006.
[2] 胡毓钜.地图投影[M].北京:测绘出版社,1981.
[3] 杨启和.地图投影变换原理和方法[M].北京:解放军出版社,1989.
[4] 李汝昌,王祖英.地图投影[M].武汉:中国地质大学出版社,1992.
[5] 祝国瑞.地图学[M].武汉:武汉大学出版社,2004.
[6] 董曼,李胜乐.世界地图等差分纬线多圆锥投影的正反解变换[J].大地测量与地球动力学,2008,28(2): 95-99.
The Transformation of Equivalent Difference Latitude Parallel Polyconic Projection on Raster Data
YE Yuanzhi
0494-0911(2012)09-0068-03
P282.1
B
2012-05-04
叶远智(1979—),男,浙江兰溪人,工程师,主要研究方向为地理信息相关系统开发应用及数字城市建设。

