基于稳健初值的抗差估计在公共点选取中的应用

肖玉兵,曾凡永,刘 毅,郭腾龙

(1.江苏省水文水资源勘测局南通分局,江苏南通226006;2.河海大学地球科学与工程学院,江苏南京210098)

0 引 言

坐标转换中经常使用最小二乘法求解转换参数,但是传统的最小二乘法适用于正态分布的样本,在数据含有较多量值不大的随机性误差情况下较为理想,但对偏离主体分布的粗差不够敏感[1]。因此,坐标转换前首先要对公共点进行筛选,剔除含有粗差的坐标值。一般的做法是首先对含有粗差的样本点进行最小二乘平差,以最小二乘的残差估值作为初值进行抗差估计,利用迭代终止时的等价权值判断粗差的位置。但这样做的问题是,含有粗差的最小二乘估值与真值存在较大的偏差,以此作为初值进行抗差估计,必然会对粗差的定位产生影响。

本文以具有稳健性的L1范数最小法为基础,验证基于稳健初值的抗差估计理论在公共点粗差定位方面的可靠性和准确性。

1 抗差估计

抗差估计法属于粗差探测理论中的“方差扩大”模型的方法,即将粗差归入随机模型,含粗差的观测值可以看作与其他同类观测值具有相同的期望,但粗差观测值的方差将异常的大。抗差估计常用的方法是选权迭代法,与传统最小二乘法不同的是,选权迭代法的权是以改正数v为自变量的等价权函数[2-3]。选权迭代法的函数模型为:

式中:P(v)应满足一定的条件,使正常观测值在迭代结束时的权不变,而含有粗差的观测值的权趋近于零,以降低含有粗差的观测值对平差结果的影响,并达到定位粗差的目的。根据权函数的不同,有不同的抗差估计方法,部分列举如下:

1.1 Huber法

Huber法的极值准则是假设观测值在不利分布情况下求最优估计,其计算公式为:

式中:Pk+1为第k+1次迭代的权函数,σ为单位权中误差,vi为观测值残差,c为常数,通常c取值在0.7至2.0。

1.2 带权数据探测法

带权数据探测法由EL-HAKIM提出,其计算公式为:

1.3 验后方差估计选权迭代法

验后方差估计选权迭代法思想是[4-5]:根据经典的最小二乘平差,求出观测值的验后方差,再利用方差检验找出方差异常大(即粗差)的观测值,然后给予它一个相应小的权进行下一次迭代平差,逐步实现粗差的定位。对于一组等精度观测值,构造式如(4)的统计量和式(5)的相应的权函数:

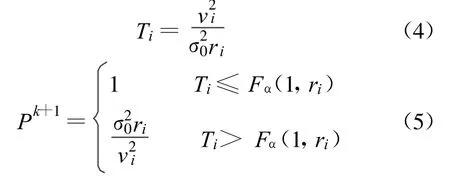
式中:σ0为单位权中误差;ri为相应的多余观测数;Fα(1,ri)为F分布的上α分位点。

2 具有稳健初值的抗差估计

选权迭代法的关键是权函数残差初值的确定,常用的做法是根据传统的最小二乘平差来确定。但是由于最小二乘估计对粗差具有均衡作用和不敏感性,有粗差的观测值的残差并非最大,致使选权迭代时发生错误的判断,当数据中的粗差较多时尤为明显[6-7]。因此应该采用一种稳健的估值方法,计算观测值的残差,提高粗差定位的稳定性。L1范数最小法的求解实际是如式(6)的线性规划问题:

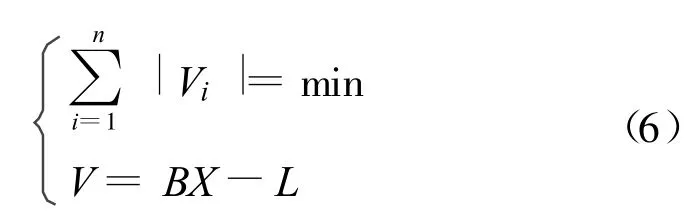
式中:X表示误差方程式的待定参数,V表示观测值的改正数。由于线性规划具有较好的稳健性,因此可利用线性规理的单纯形法求解式(6)的最佳可行解。根据最佳可行解计算坐标转换模型的残差V,作为抗差估计的初值,利用选权迭代法定位含有粗差的公共点位置。

3 计算实例

试验以某地区工程控制网为例,该区域中共有控制点12个,已知其54和80高斯平面直角坐标,为了验证本文所提方法的可靠性与准确性,选取其中五个控制点进行分析,将其编号为1,2…,5,点位分布如图1所示。坐标转换模型为式(7)所示的相似变换模型,并选取全部公共点参与计算。

图1 公共点点位分布

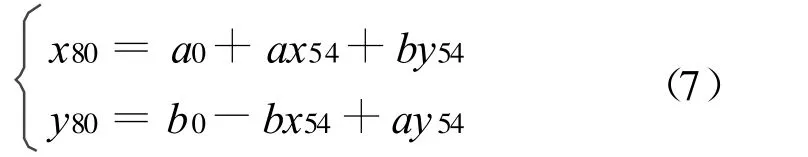
式中,(x54,y54)、(x80,y80)分别为公共点的54和80高斯平面直角坐标。为验证“具有稳定初值的选权迭代法”对公共点中粗差值定位的可靠性,设计了如下五种方案进行粗差定位的实验:

方案1:在5号点的Y坐标中加入-2 cm粗差;

方案2:在2号点的X坐标中加入-2 cm粗差;

方案3:在3号点的X坐标加入-25 cm,在4号点的Y坐标加入+20 cm的粗差;

方案4:在1号点的X坐标加入+20 cm,在5号点X坐标加入-60 cm的粗差;

方案5:在2号点的Y坐标加入+5 cm,在4号点的X坐标加入+10 cm的粗差。

以抗差估计中的带权数据探测法为例,分别以基于最小二乘初值和基于稳健初值的抗差估计法,对上述方案中的粗差进行定位。

以含有粗差的公共点坐标为观测值,以式(7)为数学模型,依次对上述方案采用经典最小二乘法进行平差,得到如表1所示的残差,并以该残差作为权函数的初值,采用带权数据探测法迭代求解,得到的等价权的最终形式如表2所示。其中表2的最后一列表示粗差定位的结果(“T”表示粗差定位成功,“S”表示只定位出一部分粗差,“F”表示粗差定位失败)。表2的最后一行列出了相应观测值的多余观测分量。

表1 L1范数最小法的转换残差(mm)

表2 基于稳健初值抗差法的等价权最终形式

分析表1可知,观测值的粗差集中反映在平差后的相应残差上,无粗差的观测值改正数则相对较小。如方案4,含有粗差的观测值为1号点的X坐标和5号点的X坐标,其改正数分别为201 mm和-600 mm,基本反映了其自身粗差值的大小,而无粗差的观测值的改正数最大只有13 mm,受粗差影响较小。

以上分析说明L1范数具有良好的稳健性,因此以L1范数的改正作为权函数的初值,进行迭代求解,如表2所示,具有粗差的观测值的权接近于0或是与其他观测值的权相差较大,取得了良好的定位效果。

4 结 语

抗差估计法定位能力的强弱与权函数的初值有很大的联系,如果权函数的残差初值能较准确地反映粗差的状况,选权迭代法的粗差定位能力将会有很大的提高。具有稳健初值的抗差估计在增加权函数初值稳定性的基础上,提高了系统的粗差定位能力。通过以上分析与比较,说明了在坐标转换中L1范数具有较高的稳健性,验证了基于稳健初值的抗差估计法在粗差探测方面的可靠性与准确性,因此,在坐标转换前利用该方法对公共点进行筛选具有较高的实用价值。

[1]景 继,王 建.基于抗差最小二乘的水工监测数据粗差探测[J].水电能源科学,2007,26(6):81-84.

[2]席志芳,楼 宇.实用性粗差检测和定位的研究[J].工程勘察,1995,(6):52-55.

[3]陈西强,黄张裕.抗差估计的选权迭代法分析与比较[J].测绘工程,2010,19(4):8-11.

[4]李德仁.利用选权迭代法进行粗差定位[J].武汉测绘学院学报,1984,(1):47-67.

[5]孙同贺,闫国庆.基于验后方差估计原理探测与剔除粗差[J].海洋测绘,2011,31(5):28-30.

[6]李 鹏.高程测量粗差探测方法与高程控制网稳定性分析[D].南京:河海大学,2005.

[7]林国庆,范东明.带权最小绝对值和法在粗差探测方面的应用[J].测绘,2010,(1):18-21.