粗糙集在洪水风险评估中的应用

张 进, 李 超, 刘孙俊

（成都信息工程学院计算机学院,四川成都 610225）

0 引言

随着计算机和网络的飞速发展,信息技术的不断发展和普及,人类积累的数据量以指数级的方式增长,并且在网络上还存在着各种丰富的数据资源。不过与数据量的增长迅速形成了鲜明的对比,人类分析数据的能力和从数据中提取知识的能力却与之存在着相当大的差距,大量的数据被收集在大型数据库中常年不被访问,造成了”数据坟墓”。因此如何有效、科学、合理、正确地应用这些数据摆在了科学家的面前,知识挖掘技术就在这个时候产生了。但是对大量数据分析和挖掘时遇到了很大的问题,大量的数据具有不完全、模糊、冗余的特性,只有很少一部分能够满足数据挖掘算法的要求,因此需要对数据进行预处理,并且需要去除其中无意义的成分,粗糙集理论由此诞生了。

粗糙集理论是由波兰杰出的数学家Z.Pawlak在1982年提出来的一种数据分析理论,刚开始时主要集中在东欧国家,当时并没有引起国际计算机界和数学界的重视,直到1990年左右该理论在数据的知识发现,模式识别,决策与分析中的成功应用才引起了各国学者的广泛关注。1991年Z.Pawlak的专著《粗糙集一关于数据推理的理论》的问世,标志着粗糙集理论及其应用的研究进入活跃时期[1-2]。

粗糙集理论是一种刻画不完整性和不精确性的数学工具,能够有效地分析和处理不完备性数据,通过发现其中的隐藏关系,从而提取出有效数据揭示其规律,简化信息处理。属性约简算法是粗糙集理论的核心内容之一。

中国是一个自然灾害频繁的国家,而洪水灾害则是对整个社会经济发展影响最大的自然灾害之一。仅仅依靠工程防洪根本无法抵御洪水的侵袭,所以在建立完善的防洪工程体系的基础上通过灾情评估,防洪调度等非工程措施对于实现防洪减灾的正规化和现代化具有非常重要的意义。洪水灾害风险评估是一项复杂的系统工程,涉及到社会,经济等诸多方面,选择洪水灾害评估指标是进行洪水灾害评估的前提和关键。此前的洪水风险评估一般都是集中在评估算法的优化,而用于评估的指标都是由专家根据经验和知识总结出来的,为了评估的准确性可能一些并没有意义或者对洪水风险评估不起作用的指标也被加入指标体系,从而导致参照的指标多达上百个,严重影响了评估算法的精确度和收敛速度。

通过对粗糙集中属性约简算法的研究,首次提出对用于洪水风险评估的指标进行约简,剔除无意义的指标,然后利用约简后的属性进行风险评估,不仅降低了专家在对指标进行打分时的模糊性,并且提高风险评估的准确性和效率[3-4]。

1 粗糙集的基本概念

粗糙集理论是处理不精确和不完备问题的数学工具,主要思想是在保持分类能力不变的前提下通过约简导出问题的分类规则。

1.1 论域等价关系和不可分辨关系

定义1 设非空集U是我们感兴趣的对象组成的非空有限集合,称为论域。

定义2 设R施U上的一个等价关系,U/R表示R的所有等价类构成的集合。

定义3 给定一个论域U和U上的一簇等价关系,若P⊆S且P≠ø,则∩P仍是论域U上的一个等价关系,称为P上的不可分辨关系,记为 IND（P）。

显然不可区分关系是一个等价关系,U/IND（P）表示不可区分关系 IND（P）在论域U上形成的一个区分,称为U的一个知识,可以简记为 U/P。

1.2 属性约简

属性约简是粗糙集理论的核心内容之一,所谓属性约简就是在保持知识库分类能力不变的前提下删除其中不相关或不重要的属性。

定义4 给定一个知识库K=（U,S）和知识库中的一个等价关系簇P⊆S,∨P∈P若IND（P）=IND（P-{R}）成立,则称知识 R为P中不必要的,否则称R为P中必要的。其中必要的条件属性组成的集合称为核。

定义5 给定一个知识库K=（U,S）和知识库中的一簇等价关系P⊆S,对任意的G⊆P,若G满足以下两条:

（1）G是独立的;

（2）IND（G）=IND（P）;

则称G是P的一个约简,记为G∈RED（P）。其中RED（P）表示P的全体约简组成的集合。

显然,知识的任何一个约简与知识本身对数据库中的任意一个范畴的表达都是等同的,即它们对论域的分类能力相同。一般而言,知识约简不唯一,可以有多种约简。

粗糙集理论对给定的对象集合由若干个属性描述,对象按照属性的取值情况分成若干个等价类,统一等价类中的对象不可区分[5]。

1.3 基于区分矩阵的属性约简算法

定义8 对于决策表 T=（U,A,V,F）,A=C∪D,C∩D=ø,C为条件属性集,D为决策属性集,可以用类似的方法计算其相对约简和相对核。

定义9 令S=（U,A,V,F）是一个只是表达系统,|U|=n,决策表S的区分矩阵是一个n*n矩阵。

基于区分矩阵的约简算法的基本过程一般如下:

（1）基于决策表生成区分矩阵;

（2）从区分矩阵中找到属性组合数为1的属性,即为核属性;

（3）从区分矩阵中找到不包含核属性的条件属性组合;

（4）将这些条件属性组合转化成合取范式的形式,并且利用吸收率进行约简;

（5）根据要求选择合适的约简。

1.4 属性约简算法的改进

因为当决策表条件属性很多时,基于区分矩阵的属性约简算法逻辑转换运算代价太大,计算复杂度很大,所以本过程利用任何一个相对约简都包含核属性这一特性对基于属性依赖度的约简算法进行改进,将大大降低计算的复杂度[6]。

根据区分矩阵中属性的特点,可以得知,区分矩阵中某个属性出现的频率越大和它所在的项越短,则该属性的潜在区分能力就会越大,该属性就会越重要

因此可以得到属性的重要性函数:

其中k为项长,指属性a是否出现在该项中,如果出现则值为1,否则值为0。该函数能够很好的体现属性的重要性,因此把其作为启发函数。

由区分矩阵可以得知,区分矩阵中的每一项与系统的约简都不为空,因为如果为空就说明该约简对该两个对象不可区分。可以根据区分矩阵中属性长度为1的作为核元素,在区分矩阵中凡是含有约简中属性的项都可以用约简代替。因此可以将这些项直接置空,从而得到过滤矩阵。

综上得到约简算法的步骤:

（1）根据构造的区分矩阵得到核元素,既项长为1的就是核元素;

（2）利用核元素对约简进行初始化,然后用约简和区分矩阵中的每一项进行与运算,将结果不为空的项删除,从而得到过滤矩阵;

（3）利用上述的启发函数对约简以外的属性计算重要性,将属性重要性最大的属性加入到约简中;

（4）计算约简与区分矩阵中每一项的交集,如果为空则结束,否则转到（3）;

（5）返回约简。

2 应用粗糙集理论的洪水风险评估介绍

首先应该选定进行洪水风险评估的特定地区,这里选定武汉市作为洪水风险评估的区域。

2.1 洪水风险评估的指标集的选取

通过询问专家和实地调查得到可能影响该地洪水风险的因子包括:地形,植被,土壤含水量,降雨,水库分布,人口密度,耕地面积,人均收入水平,水利设施建设,防灾意识,河网密度,年龄结构,健康状况,教育程度,基础设施密度,生产总值等。

2.2 根据当地历年的指标值和结果值构造决策表

通过查询1991～2005年《中国城市统计年鉴》中武汉市当时相关统计数据和中国气象科学数据共享服务网中暴雨洪涝灾害数据集、中国地面国际交换站气候标准值年值数据集、中国农作物生长发育和农田土壤湿度旬值数据集得到武汉市对应各属性的数值。

表1是通过对上述查询数据进行一致性处理:即根据一定的标准划分等级,这里采用中华人民共和国水利部于1994年6月2日发布的防洪标准（GB50201-94）,其中决策属性划分为特大洪水,大洪水,小洪水,无4个等级;而条件属性则根据防洪标准划分为4个等级,然后再根据等级数据构造洪水信息决策表。

表1 历年洪水信息决策表

2.3 根据决策表构造对应的区分矩阵

根据区分矩阵的定义,可以知道区分矩阵具有如下性质:首先,区分矩阵是一个对称矩阵,因此只需要计算上三角矩阵或者下三角矩阵就可以了。其次可以根据定义得知区分矩阵的元素内容是由区分两个对象的属性构成的:当两个对象的条件属性和决策属性完全相同时,则它们所对应的区分矩阵的元素为0;当两个对象可以通过条件属性取值不同加以区分时,则它们所对应的区分矩阵元素取值为这两个对象不同的条件属性集合;当这两个对象的所有条件属性取值相同而决策属性取值不同时,则对应的区分矩阵中的元素取值为空。

表2是根据历年洪水信息决策表构建的区分矩阵,由于区分矩阵是对称矩阵,所以这里只计算了下三角矩阵。

表2 区分矩阵

2.4 根据区分矩阵得到核属性

从区分矩阵中找到属性组合数为1的条件属性,则这些条件属性的组合即为核属性,得到的核属性是降雨,将核属性加入到约简集中。

2.5 将约简集和区分矩阵中的每一项进行与操作,从而得到约简矩阵

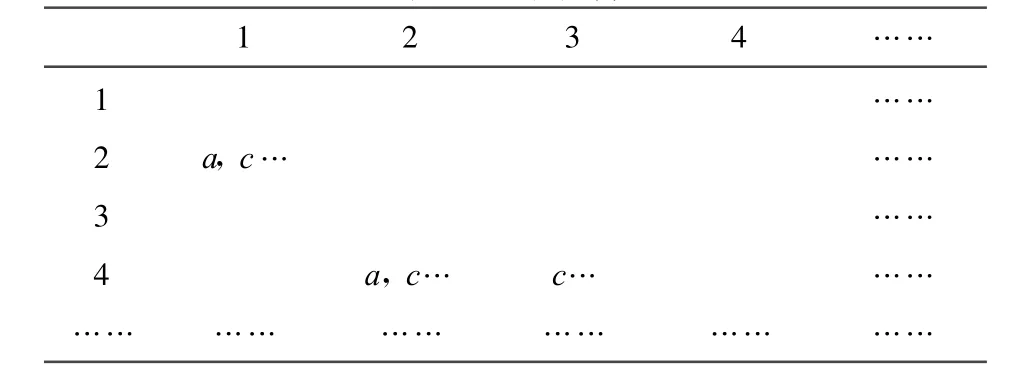
表3 过滤矩阵

表3就是用约简集和区分矩阵中的每一项进行与操作后得到的过滤矩阵,然后根据过滤矩阵计算矩阵中所有属性的重要性:

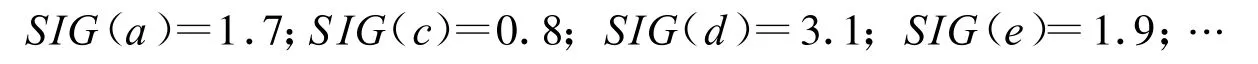
由以上计算可知,在过滤矩阵中重要性最大的是d（国民生产总值）,因此将d加入到约简集中,然后再次用约简集与过滤矩阵相交,得到新的过滤矩阵,再按属性的重要度依次将属性加入到约简集中,直到约简集与过滤矩阵的相交为空,返回约简集。

得到的相对约简包括的条件属性:降雨,国民生产总值,植被覆盖率,人口密度,财产密度,基础设施密度,中小企业密度,防洪设施建设。

2.6 将条件属性约简作为指标集,构建层次的洪水风险评估指标体系

由于在此应用的是粗糙集的基于区分矩阵的约简算法,能够得到所有约简,因此这里还需要专家根据经验选择合适的约简作为指标集构建风险评估指标体系。用约简的结果和以前一些用于洪水评估的指标进行对比,不难发现条件属性中土壤含水量,地势,国民受教育程度等因素都没有被用于构建评价指标体系。因为根据武汉市的历史资料发现这些因素对武汉市的洪水灾情并没有起到作用,因此在这里对这些因素进行了删除,以免影响后面进行的风险评估。

图1是武汉市的洪水风险评估的指标体系,分为3层结构:第一层是该地区的洪水风险等级;第二层是因素集;第三层是子因素集。

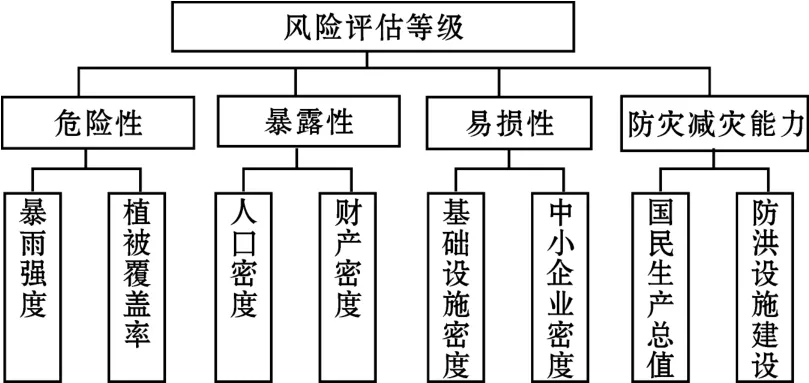
图1 洪水风险评估的指标体系

2.7 运用模糊层次分析法在构建的评估指标的基础上对该地区的洪水风险进行评估

根据模糊层次分析法所建立的数学评估模型如下:

其中F为系统总得分,C为系统评估矩阵;S为专家评定的洪水风险的安全等级加权值;A为指标体系第二层的因素权重分配集;B为由Bi组成的总评估矩阵;Ai为第三层子因素的权重分配集;Ri各因素对应的评估矩阵,是由专家根据评语集即表4投票得出的[7-8]。

表4 洪水风险等级加权值

表5 洪水风险等级

应用模糊层次分析法进行洪水风险评估介绍:

（1）要采用层次分析法确定武汉市洪水评估指标因素的权重值:洪水风险评估指标体系递减层次结构的构成确定了上下级之间的关系,可对每一层次各个因素相对于上一层某一准则的重要性进行两两比对,从而构造出判断矩阵。其中表6是因素层中各因素对于系统的权重所建立的判断矩阵,求得的权重集是（0.45,0.27,0.10,0.18）。类似还需要求出子因素层中各子因素对于因素层中对应因素的权重判断矩阵,并且求出权重集。

表6 判断矩阵

（2）求得武汉市洪水风险的总得分:利用表4根据所建立的模糊层次评估模型计算得到的武汉市的风险评估得分为51。

（3）确定武汉市洪水风险等级:根据表5,武汉市的风险的风险评估得分为51属于45-59范畴,因此风险等级为较差。

查看了武汉市2005年至今的洪水灾害损失情况都是比较严重的,其中重大洪水两次,排在了全国城市洪水损失的前列,可见评估得到的结果与武汉市的现实情况基本相符。因此在对武汉市的洪水风险进行评估时利用粗糙集约简理论对用于评估的属性集进行约简,利用约简后的属性进行风险评估,最终的结果是可靠的。由此可见土壤,地势等属性对于武汉市的洪水风险评估是多余的,是可以剔除的,并不影响最终评估结果的准确性。

3 结束语

运用粗糙集理论的基于区分矩阵的改进的属性约简算法对洪水风险评估中的指标集进行了约简,得到了在洪水风险评估中起作用的指标,剔除了无意义的指标,比传统的专家投票等单纯依靠经验的方法具有科学依据和数据支持。由于指标数量减少更易于专家对各个指标进行打分,提高了区域洪水风险评估的准确性和效率。因为应用粗糙集的属性约简算法需要大量的样本数据,当数据量不充足时可能会导致最终的结果出现偏差,所以在应用粗糙集的属性约简算法时应该保证样本数据的正确性和充分性。

[1] 张文修,吴伟志,梁吉业,李德.粗糙集理论与方法[M].北京:机械工业出版社,2002.

[2] 殷杰,柴毅,郭茂耘.应用粗糙集提取柴油机故障数据特征[J].计算机工程与应用,2011,（29）.

[3] 刘新立.区域水灾风险评估的理论与实践[D].北京:北京师范大学,2000.

[4] 王保生,江西旱涝灾害风险评估与农业可持续发展[J].同济大学学报（自然科学版）,2005,（8）:31-34.

[5] 梁蒙.基于粗糙集的属性约简算法研究[D].河南:河南大学,2011.

[6] 赵永安.基于粗糙集的属性约简算法研究[D].内蒙古:内蒙古大学,2008.

[7] 王为人.基于层次分析法的流域水资源配置权重测算[M].北京:中国林业出版社,1998.