基于集成计数器的N进制计数器设计与仿真
赵家松,周 兵,严伟榆
(云南农业大学 基础与信息工程学院,云南 昆明 650201)
基于集成计数器的N进制计数器设计与仿真
赵家松,周 兵,严伟榆
(云南农业大学 基础与信息工程学院,云南 昆明 650201)
计数器是一种重要的时序逻辑电路,广泛应用于各类数字系统中。介绍以集成计数器74LS161和74LS160为基础,用归零法设计N进制计数器的原理与步骤。用此方法设计了3种36进制计数器,并用Multisim10软件进行仿真。计算机仿真结果表明设计的计数器实现了36进制计数的功能。基于集成计数器的N进制计数器设计方法简单、可行,运用Multisim 10进行电子电路设计和仿真具有省时、低成本、高效率的优越性。
电路设计;仿真;计数器;归零法;Multisim10
计数器是记忆时钟脉冲个数的数字电路,作为一种最典型的时序逻辑电路,在各类数字系统中有着广泛的应用。计数器的设计方法主要有两种,1)以时钟触发器为核心加上必要的门电路进行设计[1-2];2)利用集成计数器构建,这种方法从设计原理到硬件实现都相对简单,因而较为常用。基于集成计数器的N进制计数器设计方法有归零法和置数法。文中以最常用的4位二进制(十六进制)同步加法计数器74LS161及十进制同步加法计数器74LS160为核心,以三十六进制为例,介绍了归零法设计N进制计数器的方法,并用Multisim10软件进行仿真。Multisim10软件由美国国家仪器(National Instruments,NI)公司于2007年推出,该软件具有以下特点:1)直观的图形界面;2)庞大的元器件库;3)丰富的测试仪器;4)完备的分析工具;5)强大的仿真能力;广泛应用于电子电路 的 教 学[3]、设 计[4-5]和 科 研[6]中 。
1 归零法设计原理
1.1 集成计数器功能描述
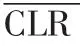

表1 74LS161状态表Tab.1 State table of 74LS161
十进制同步加法计数器74LS160的状态表与74LS161类似,区别在于计数状态是按十进制(8421BCD码表示)规律变化。
1.2 归零法设计原理
设现有M进制集成计数器,设计N进制计数器。若M>N,从全零初始状态S0开始计数,第1个时钟到来时,计数状态为S1,第N-1时钟到来时,计数状态为SN-1,第N时钟到来时,利用集成计数器的清零端或是置数端,使计数状态返回全零初始状态S0,原M进制集成计数器中的SN~SM-1这M-N个状态被跳过。若集成计数器的清零端为异步控制方式,具体设计与仿真步骤为:
1)确定最大计数状态SN(过渡状态),并写出SN的二进制代码;
2)根据状态SN的非完全译码,求归零逻辑,即清零端控制信号的逻辑表达式;
3)在仿真平台Multisim中选择器件,根据归零逻辑创建仿真电路;
4)选择时钟信号源输入,示波器或数码管等作为测量或显示仪器,运行仿真电路,观测结果。
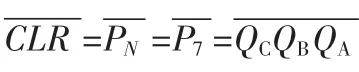

图1 七进制加法计数器仿真电路Fig.1 Simulation circuit of modulo-7 adding counter
用归零法设计N进制计数器要注意以下两点:
1)当集成计数器的清零端为同步控制方式,则不会出现过渡状态SN,此时最大计数状态应为SN-1,相应归零逻辑也由SN-1求得。
2)若M 74LS161为十六进制计数器,设计三十六进制计数器需要两个74LS161通过级联的方法,可先扩展成256(16×16)进制计数器。设低位的74LS161编号为1,高位的74LS161编号为2,再用归零法设计如下: 1)写出SN的二进制代码:SN=S36=100100; 3)在仿真平台Multisim中选择2个74LS161,1个74LS00,2个5 V电源和地,根据归零逻辑创建仿真电路; 4)时钟电压源V1接入计数脉冲输入端CLK,用带译码的十六进制数码管U4和U5作状态输出的显示器,完整的三十六进制计数器仿真电路如图2所示。 图2 基于74LS161的三十六进制加法计数器仿真电路Fig.2 Simulation circuit of modulo-36 adding counter based on 74LS161 运行仿真电路,在时钟控制下,数码管U5和U4以2位十六进制数方式循环显示 00,01,02, …,09,0A,0B, …,0F,10,11,…,23,00,…,共 36 种输出状态,本质上是 8 个计数输出端Q2D~Q2AQ1D~Q1A对应二进制代码以00000000,00000001,…,00100011,00000000,…,循环变化,共36种输出状态。 因此,图2电路用74LS161实现了三十六进制加法计数功能。 74LS160为十进制计数器,其计数状态QDQCQBQA以8421BCD码的方式输出,最大状态为1001。设计三十六进制计数器需要2个74LS160通过级联的方法,可先扩展成100(10×10)进制计数器。设低位的74LS160编号为1,高位的74LS160编号为2,再用归零法设计如下: 1)写出 SN的 8421BCD 码:SN=S36=(00110110)8421BCD; 3)在仿真平台Multisim中选择2个74LS161,1个74LS20,2个5 V电源和地,根据归零逻辑创建仿真电路; 4)时钟电压源V1接入计数脉冲输入端CLK,用带译码的十六进制数码管U4和U5作状态输出的显示器,完整的三十六进制计数器仿真电路如图3所示。 图3 基于74LS160的三十六进制加法计数器仿真电路Fig.3 Simulation circuit of modulo-36 adding counter based on 74LS160 运行仿真电路,在时钟控制下,数码管U5和 U4以2位十进制数方式循环显示 00,01,02,…35,00,…,共 36 种输出状态,本质上是8个计数输出端Q2D~Q2AQ1D~Q1A对应8421BCD码以初态00000000,随着时钟的到来依次加1,直到00110101,00000000,…,循环变化,共36种输出状态。因此,图3电路用74LS160实现了三十六进制加法计数功能。 计数状态以十进制数方式显示,读数方便,符合多数人的习惯。若无十进制计数器74LS160,用十六进制计数器74LS161也可构成以十进制数方式显示的三十六进制加法计数器,但设计较为复杂。以下介绍一种设计方法。 1)确定级联逻辑:共需要2个74LS161,设低位的74LS161编号为1,高位的74LS161编号为 2,采用与图2和图3同样的同步级联方式,即外接脉冲同时接入高、低位2个74LS161的计数脉冲输入端CLK。低位74LS161的计数控制端ENP和ENT都接高电平,即ENP1=ENT1=1,使其工作于计数状态。因为要采用十进制数方式显示,则低位74LS161最大输出状态1SN-1=1S9=Q1DQ1CQ1BQ1A=1001,此时其进位输出RCO1=0,不能用于控制高位74LS161进行计数。高位74LS161的计数控制端ENP和ENT可由低位最大状态的非完成译码控制,即ENP2=ENT2=Q1DQ1A。设初态为全零状态,每来一个时钟,低位74LS161记一次数,状态代码加1,第9个时钟到来后,高位74LS161计数控制端有效,第10个时钟到来,低位74LS161清零的同时,高位74LS161记一次数。 4)在仿真平台Multisim中选择2个74LS161,74LS00、74LS04、74LS20各1个,2个5 V电源和地,根据归零逻辑创建仿真电路; 5)时钟电压源V1接入计数脉冲输入端CLK,用带译码的十六进制数码管U6和U7作状态输出的显示器,完整的三十六进制计数器仿真电路如图4所示。 图4 基于74LS161的三十六进制加法计数器仿真电路(十进制数显示方式)Fig.4 Simulation circuit of modulo-36 adding counter based on 74LS161,displaying with decimal mumber 运行仿真电路,在时钟控制下,数码管U7和 U6以2位十进制数方式循环显示 00,01,02,…35,00,…,共 36 种输出状态,显示结果与图3电路显示相同。因此,图4电路用74LS161实现了以十进制数方式显示的三十六进制加法计数功能。 计数器具有计数、分频、定时等功能特点,广泛应用于数字测量、控制等数字系统,掌握N进制计数器的设计方法有着理论和实践意义。文中以集成计数器74LS161和74LS160为基础,采用归零法,多方式地实例设计了36进制计数器,设计原理清晰,逻辑严谨;电路简单,易于实现。应用Multisim 10进行电子电路设计和仿真,可用大量丰富的元器件库和实用的虚拟仪器,操作简单,搭建电路方便、快捷,并且修改电路方便,是现代电子设计的有效方法。基于集成计数器的N进制计数器设计方法有推广价值,用非十进制集成计数器设计以十进制数方式显示的N进制计数器有创新性。 [1]余孟尝.数字电子技术基础简明教程[M].3版.北京:高等教育出版社,2006. [2]孙宏国.N进制计数器的几种设计方法及比较 [J].电气电子教学学报,2002,24(4):54-55,62. SUN Hong-guo.Several design methods of modulo-N counter[J].Journal of EEE,2002,24(4):54-55,62. [3]张亚君,陈龙,牛小燕.Multisim在数字电路与逻辑设计实验教学中的应用[J].实验技术与管理,2008,25(8):108-110,114. ZHANG Ya-jun,CHEN Long,NIU Xiao-yan.Application of Multisim in digital circuit and logic design experiment teaching [J].Experimental Technology and Management,2008,25(8):108-110,114. [4]赵家松,黄荣华,严伟榆.基于Multisim10的电子摇号器设计与仿真[J].电子设计工程,2011,19(13):124-126,130. ZHAO Jia-song,HUANG Rong-hua,YAN Wei-yu.Design and simulation on electronic numerical selection generator based on Multisim10 [J].Electronic Design Engineering,2011,19(13):124-126,130. [5]董玉冰.基于Multisim9.0简易数字频率计的设计与仿真[J].长春大学学报,2009,19(6):6-8,18. DONG Yu-bing.The design and simulation of simplified digital frequency counter based on Multisim9.0[J].Journal of Changchun University, 2009,19(6):6-8,18. [6]樊彬,周铁戈,阎少林,等.Multisim在超导器件研究中的应用[J].电子学报,2010,38(8):1886-1891. FAN Bin,ZHOU Tie-ge,YAN Shao-lin,et a1.The application of multisim in superconductive electronics[J].Acta Electronica Sinica, 2010,38(8):1886-1891. [7]杨颂华,冯毛官,孙万蓉,等.数字电子技术基础[M].西安:西安电子科技大学出版社,2000. [8]万旭.计数器的级联规律及其应用[J].浙江师大学报:自然科学版,2000,23(1):40-44. WAN Xu.The laws and its application of counters’cascade[J].Journal of Zhejiang Normal University:Natural Science Edition, 2000,23(1):40-44. Design and simulation on modulo-N counter based on integrated counter ZHAO Jia-song, ZHOU Bing, YAN Wei-yu Counter is a kind of important sequential logic circuit model.It has been widely used in a variety of digital systems.A design method of modulo-N counter with integrated counter is presented.Three kinds of modulo-36 counter are designed and simulation by this method.The computer simulation results show that the design implements modulo-36 counter.The design method of modulo-N counter with integrated counter is simple and feasible.This design and simulation based on Multisim10 has many advantages, such as time-saving, 1ow in cost and efficient. circuit design; simulation; counter; reset zero method; Multisim10 TN79+1;TP391.9 A 1674-6236(2012)04-0027-04 2011-12-31 稿件编号:201112170 云南省教育厅科学研究基金项目(09C0284) 赵家松(1975—),男,云南昭通人,硕士,讲师。研究方向:电子信息,网络通信工程。2 三十六进制加法计数器的设计与仿真
2.1 基于74LS161的三十六进制加法计数器的设计与仿真

2.2 基于74LS160的三十六进制加法计数器的设计与仿真

2.3 基于74LS161的三十六进制加法计数器的设计与仿真(以十进制数方式显示)


3 结束语
(School of Science and Information Engineering,Yunnan Agriculture University,Kunming650201,China)

