两类新的GM(1,1)残差优化模型的建立及预测

何 光，卢小丽

0 引言

灰色系统解决了小样本及信息不全的问题，大量应用于生产生活领域，引起了广泛的关注。灰色模型即利用离散随机数，生成为较有规律的生成数，进而建立起的微分方程模型。提高灰色模型的可靠性及预测精度一直处于不断的实践和探索中。目前，已有文献通过残差修正模型[1]、对初始数列的变换[2-5]及建立背景值修正的不等时距模型[6]等方式改进模型预测的精度。然而在已有结论中，大多数只侧重于分析某一方面（如残差修正、初始数列的变换或背景值修正等）的改进，而对于多方面的融合探讨少有涉及。

在文[1]中提出的残差修正模型基础上，本文将结合函数变换的思想，建立新的GM(1,1)残差优化模型，以提高预测的精度和可靠性。

1 GM(1,1)模型及预测

设n个元素的初始数列x(0)=(x(0)(1),x(0)(2),…,x(0)(n))的AGO生成数列为

其中，a称为发展系数，b称为灰作用量，z1(k)称为白化背景值。

如果将x(0)(k)各时刻k视为连续变量t，则x(1)就可视为t的函数。记x(1)=x(1)(t)，x(0)(k)对应于导数dx(1)/dt，背景值z(1)(k)对应于x(1)(t)，则有GM(1,1)灰微分方程对应的白微分方程：

该方程称为GM(1,1)的白化型。如果白化型模型的精度高，则表示所建立的GM(1,1)与真正的微分方程拟合较好。

结合GM(1,1)模型进行灰色预测，步骤如下。

第一步：由初始序列x(0)=(x(0)(1),x(0)(2),…,x(0)(n))，得一次累加生成序列x(1)。

第二步：求x(1)的白化微分方程中的待定参数a和b，即[a ,b]T=[BTB]-1BTyn。

其中

第三步：将参数a,b代入还原后的模型，得到x(1)的估计值：

进而计算出 x(0)(k)的估计值 x̂(0)(k+1)=x̂(1)(k+1)-x̂(1)(k)。

第四步：模型检验。分别计算残差检验、关联度检验和后验差检验的相应指标，如符合精度要求，则可用于预测；否则，运用残差修正模型加以改进。

2 已有的GM(1,1)残差修正模型

2.1 传统的GM(1,1)残差修正模型

在灰色预测的模型检验中，若残差检验不合格时，需建立残差修正模型。设残差q(0)(k)= | x(1)(k)-x̂(1)(k)| ，得残差列

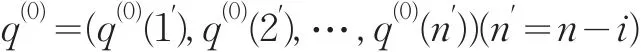
对q(0)建立GM(1,1)模型，将得到的预测值处理后，加入原模型得残差修正模型：

根据i的取值差异得到不同的残差修正模型。

2.2 改进的残差修正模型

文[1]中提出了两种改进的残差修正模型：模型I和模型II。

模型 I：设残差为 q(0)(k)=x(0)(k)-x̂(0)(k)，对 q(0)建立GM(1,1)模型，将得到的预测值，加入原模型得修正模型：

模型II：设残差为q(0)(k)= | x(0)(k)-x̂(0)(k)| ，对 q(0)建立GM(1,1)模型，将得到的预测值，加入原模型得修正模型：

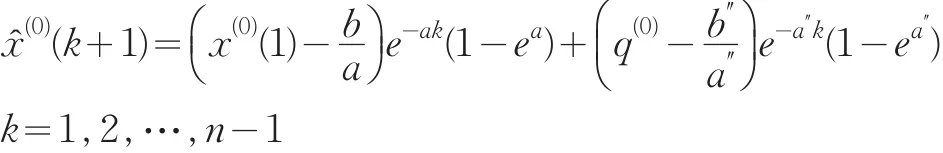
3 两类新的GM(1,1)残差修正模型

邓聚龙教授指出建立GM(1,1)模型的前提是初始数列x(0)为光滑离散函数[7]。x(0)的光滑性决定了模型预测的可靠性和精确度。于是结合已有的残差修正模型，通过对预测数列先进行光滑度的处理，然后作灰色建模和预测。

残差优化模型1的具体步骤如下：

第一步：对初始序列x(0)进行光滑度处理，得到序列w(0)。可选用以下方案：

(1)对数函数转化T1:ln x(0)(k)；

(2)幂函数转化T2:(x(0)(k))t,t∈(0,1]；

另外，还可以考虑负指数函数、负指数函数-幂函数转化等方法。

第二步：对w(0)建立GM(1,1)模型，然后利用函数转化的逆运算，将其预测值 ŵ(0)还原为 x̂(0)。

第三步：设残差为q(0)(k)= | x(0)(k)-x̂(0)(k)| ，对 q(0)建立GM(1,1)模型，将得到的预测值，加入原模型进行修正。

在优化模型1的基础上，还可以进一步改善残差，得到优化模型2。具体步骤如下：

第一步：对初始序列x(0)进行光滑度处理，得到序列w(0)。

第二步：对w(0)建立GM(1,1)模型，然后将其预测值ŵ(0)还原为 x̂(0)。

第三步：设残差为q(0)(k)= | x(0)(k)-x̂(0)(k)| ，对残差序列作光滑度处理后，再建立GM(1,1)模型；最后将得到的结果还原处理后，加入原模型予以修正。

4 应用实例

以文[1]中Fibonacci数列为例，初始数列为：x(0)={x(0)(k)}={1,1,2,3,5,8,13}，其中 k=0,1,2,…,6。易知该数列为光滑的[8]，可用灰色模型进行预测和分析。根据文[1]的结论，作者提出了两种改进的误差修正模型对数列x(0)做出预测，其结果在精度上要优于传统的残差修正模型，其中第二种改进模型效果更好。这里我们将运用优化模型1对数列x(0)进行预测，并与文[1]中的结果进行比较。

首先，分别运用T1、T2和T3对 x(0)进行光滑度处理。运用T1和T3时，为使运算有意义，需先将原数列化为 y(0)(k)=x(0)(k)+3后，再进行灰色预测，最后用x(0)(k)=y(0)(k)-3还原；运用T2和T3时，取t为0.5。

然后通过优化模型1，可分别得出三种处理方式的预测情况，见表1。

表1 三种光滑度处理方法的预测结果

从表1中数据可看出，选用T2处理后，除x(0)(1)=1的预测值误差过大外，对其余各项x(0)(k)(k=2,3,…,9)的拟合情况明显优于T1和T3；并且这种精度优势从预测项k=7开始，表现的尤为突出，体现出预测结果的可靠性高。综合比较下，选择T2作为初始数列x(0)的光滑度转换方式，并将结果与文[1]中预测效果最好的模型II比较，见表2。

由表2中的比较结果可知，本文所建立的优化模型1的平均相对误差为4.38%，与文[1]中模型II的5.13%相比，有明显的改进。同时从图1中可看出，当k＞2时，优化模型1的残差绝对值均小于或等于文[1]中的模型II的结果，其拟合精度更高。而且对于k=7的预测项，优化模型1的相对误差绝对值仅为0.05%，远小于1%，与文[1]中模型II的3.16%相比，其预测的可靠性更强。

表2 两种改进模型的预测结果比较

图1 两类模型的残差比较

综上所述，经过一次光滑度处理得到的优化模型1无论从整体的误差率方面，还是在预测前景上，均优于文[1]中的模型II。最后，考虑优化模型2，模型2的两次光滑度处理均采用幂函数转化。通过实验分析得，在初始数列的处理中取t=0.5，以及在残差序列的处理中取t接近1（如t=0.05）时，拟合效果较好。其预测情况与优化模型1比较，见表3。

表3 优化模型1和2的预测情况比较

表3中，从整体情况分析，由前7项的拟合值，可计算出优化模型1和2的平均相对误差分别为4.38%和4.15%，模型2的误差率较低；而由前9项拟合效果看，模型2的误差率也低于模型1。表明经过两次光滑化处理后，模型2的精度比模型1有一定的提高，略优于模型1。当3＜k≤9时，两类模型相对误差的绝对值均控制在1%以内，精度很高；特别是在k＞6以后的预测值，结果令人满意。

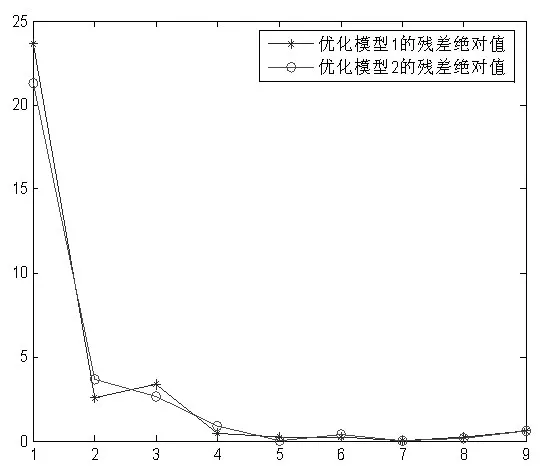
图2 优化模型1和2的残差比较

另外，从两类模型的残差绝对值（图2）情况可看出，随着预测项数的增大，当k＞5时，两者的预测数据差异不大。表明优化模型2在预测方面比模型1的优势并不明显，仍有值得改善和思考的地方。

5 结论

在文[1]提出的改进残差修正模型的背景下，运用函数转化先对初始数列进行光滑度处理，得到优化模型1；然后在模型I的基础上，进一步对残差序列也作光滑度处理，得到优化模型2。然后通过实例，将优化模型1和2与文[1]中的模型II比较，结果分析如下。

第一，与文[1]中的改进模型相比，优化模型1不仅在平均相对误差上更低，而且其优势在预测值方面体现得更明显，未来预测值的精度和可靠性均优于文[1]的模型II；

第二，优化模型2比优化模型1的平均相对误差有进一步的改进，特别在预测方面，模型2的结果优于模型1；

第三，在实例中，优化模型1和2中的光滑度处理均选择了幂函数进行转换，当面对不同问题时，需要根据具体情况选择合适的函数转换。

[1]王明礼.三种灰色系统模型的预测比较[J].统计与决策，2011,(8)．

[2]何斌,蒙清.灰色预测模型拓广方法研究[J].系统工程理论与实践,2002,22(9)．

[3]陈涛捷.灰色预测模型的一种拓广[J].系统工程,1990,8(7)．

[4]李群.灰色预测模型的进一步拓广[J].系统工程理论与实践,1993,13(1)．

[5]王建根,李春生.灰色预测模型的一个注记[J].系统工程,1996,14(6).

[6]江安,王金山,王鹏.一种改进的灰色预测模型[J].佳木斯大学学报（自然科学版），2011，29(2)．

[7]邓聚龙.灰色系统的GM模型[J].模糊数学,1985,4(2)．

[8]邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002．