倒U型多拐点社会问题的测度

罗爱华

0 引言

收入分配是人文社会科学领域一大重要课题，社会学家通常从促进社会公平和稳定的角度阐述收入分配不平等的危害。而在经济学领域，学者们更多的是探究收入分配不平等对消费、总收入等经济变量的影响。过去半个多世纪以来，学者们就经济增长与收入不平等之间互动因果关系进行了大量探讨，所得理论成果也是百家争鸣。库兹涅茨在其论文《经济增长与收入不平等》中将收入分配不平等视为解释变量，经济发展水平为被解释变量，利用英、美、德等多国数据推论出其著名的“倒U型假说”。倒U型假说揭示每一经济体在经济发展过程中所显示出的共通规律：在经济发展初期，收入差距将随着经济发展水平上升而扩大，而当经济发展到一定阶段后，收入差距将随经济发展水平上升而缩小。“倒U型假说”似乎完美地解说了一个经济社会良好的发展轨迹，但这半个多世纪以来关于此假说的争论一直未停止过。反对者主要是针对库兹涅茨使用的数据等方面进行质疑，表示其推论不一定具有普适性。

本文在研究中采用的是计量经济学领域较为前沿的拟合倒U曲线的研究方法，事先不假定收入分配不平等与基尼系数之间的关系，利用重庆城镇收入不平等、经济发展数据，使用非参数局部多项式进行函数拟合，对倒U假说进行验证。

1 理论模型

1.1 非参数局部多项式回归模型

对于基尼系数和人均GDP（或其值的对数值）函数关系拟合学者们一直都有深入的研究，本文采用的是计量经济学领域较为前沿的模型分析方法，非参数局部多项式回归模型。非参数局部多项式回归模型是非参数回归模型的一种。

给定n对观察值（X1,Y1）（X2,Y2）…（Xn,Yn）,自变量X和因变量Y之间的关系由下面方程定义：

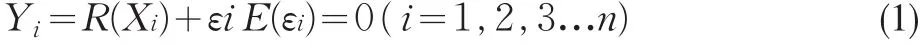
这里的R(x)为回归函数，Rn(Xi)为其估计值。对该回归函数的估计有多种方法，核估计便是其中常见的一种。核估计条件下，选择一个估计量a=Rn(Xi)使得

最小。其中W(Xi)=K((Xi-x)/h)为核函数，h为带宽，即在x领域内选择多大的带宽以包含参与回归估计的点。核函数的种类较多，但研究表明选择不同核函数进行估计其估计值差别不大，真正影响非参数回归估计精准性的是带宽的选择。然而传统的核估计也不是非参数回归最佳的选择，因为核估计存在边界效应，即边界处收敛于实际函数的速度慢于内点处的收敛速度，同时核估计带来的估计误差较大，偏差与自变量的密度函数有关。相比经典的N-W核回归估计，局部多项式估计方法均可避免上述问题。另外，局部多项式估计方法既适用于解释变量为确定性变量的固定设定模型，也适用于解释变量为随机性变量的随机设定模型；既适用于随机设定模型解释变量分布均匀的情形，也适用于分布不均匀的情形。此外，局部多项式估计还可估计出回归函数的导函数、二阶导等（取决于多项式的阶数），方便进行经济学领域内的边际效益、弹性分析等。局部多项式估计拥有的诸多优点使该项回归方法近年来备受计量经济学各领域学者的青睐。

在应用非参数局部多项式估计方法时，针对曲线上不同X0点进行泰勒展开。假设收入分配不平等为变量y,经济增长为变量x,倒U曲线函数形式未知，但我们可以表示为一般形式：y=m(x)。

对于每一x点我们都按泰勒展开式展开：

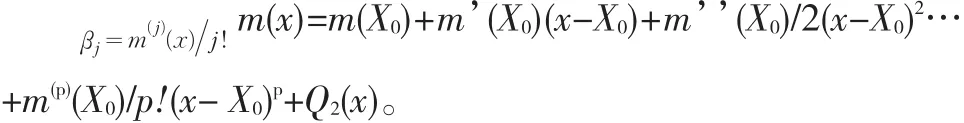
Q2(x)可看成是随机误差，令

X0的选择可以是任意的，显然我们的估计值m(X0),m’(X0),m’’(X0)/2…m(p)(X0)/p!与X0有关。非参数二项式估计方法同核估计方法本质相同，要求下式取得最小值：

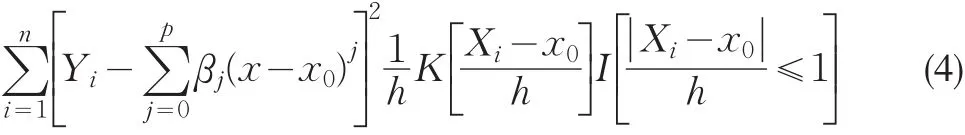
其中，K(x)是核函数，I(x)是显示函数。核函数为每一参与局部多项式回归的观测点赋予权重，显示函数的含义则是当括号内的不等式成立时函数值取1否则取0，由此确定X0邻域内参与高点局部多项式回归的观测点。其中Y=（Y1，Y2，...，Yn）T；β =（ β1，β2，...，βn）T；W=Diag

由此，上式的加权最小二乘解为：

1.2 回归模型的几点说明

非参数局部多项式回归模型中涉及到的几个比较重要的因素是窗宽h、核函数及阶数p的选择。

（1）最佳窗宽的选择

窗宽参数h在局部回归中影响到参与回归的观测点个数，太大的窗宽将使与x=X0距离较远的点也参与回归，而太小的窗宽则使领域内较少的点参与局部回归，这两者都会使估计结果与真实值有较大偏差。因而寻求最佳窗宽是本研究重要任务之一。最佳窗宽的估计原理是在每个观察点Xn处，剔除该点对其余n-1个点进行核权估计，最终选择平均拟合误差达最小的窗宽h。本研究中，在寻找最佳窗宽过程中，首先采用系统默认值发现模型拟合效果较差。最后通过在R软件中进行编程求得最佳窗宽0.513，此时模型拟合性状较优。

（2）核函数的选择

核函数为一个对称的概率密度函数，它在局部回归中的意义是起到平滑的作用。具体到每一观测点X0来讲，在进行局部回归时对参与回归的X0领域内观测点赋予权重，与X0距离近的观测点赋予较大权重;相反则赋予较小权重，从而能够消除随机因素影响，使模型拟合结果更符合实际情况。而实际上在局部多项式回归当中，不同核函数的选择对估计结果的影响不是特别大。因此，本研究中核函数选用的是系统默认的高斯核函数。

（3）阶数p的选择

对于给定的窗宽h，阶数越大局部多项式回归的估计偏差越小，但同时也导致了较大的方差。本文在研究中主要考虑到局部多项式回归常数项、导数项、二阶导数项对于经济学中的弹性分析、拐点分析，能够更好地反映函数的性态，因此p选择了二次多项式回归。

2 实证分析

2.1 基尼系数源数据采集与计算

基尼系数的计算有多种方法，而本研究的重点在探讨基尼系数与人均GDP之间的关系，因此基尼系数的计算采取相对较为简单便捷的公式法。根据《重庆统计年鉴》里关于城镇人口收入分组调查数据，我们可以选择下述公式进行计算：

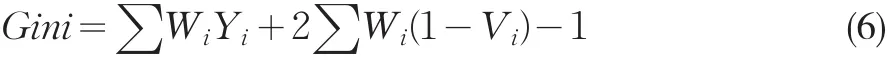
其中，Wi是按收入分组后的人口数占总人口数的比重，Yi是按收入分组后各组人口所拥有的收入占收入总额的比重，Vi是Yi从i=1的累计数即Vi=Y1+Y2+⋅⋅⋅Yi[4]。

本研究收集到1989～2009年《重庆市统计年鉴》中关于城镇人口收入分组数据，由此针对每一年的收入分组数据进行计算得到历年的城镇基尼系数值。在计算中，公式里有些参数大都是不能直接得到，如Wi需要根据每一分组所占的户数及户人均人口来计算，Yi、Vi则都要根据户数、户人均人口及人均可支配收入来计算。表1给出了1989～2009年计算出的基尼系数值。

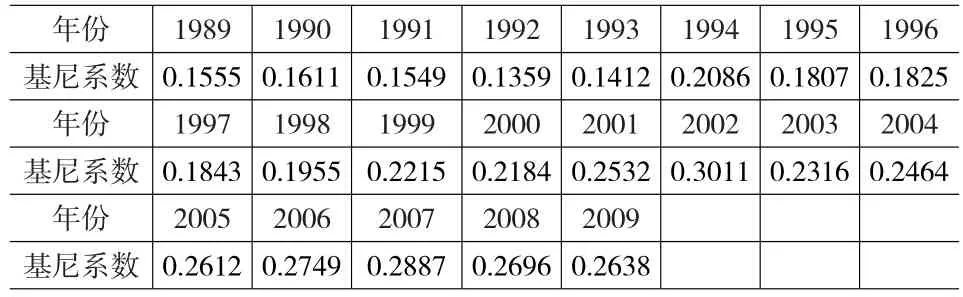
表1 1989年到2009年基尼系数值

需要说明的是有些年份（1996、2006）的基尼系数源数据统计上有明显错误，因此选取其前后两年的基尼系数的算术平均值。对比学者陈昌兵计算出的1995年到2004年的重庆城镇居民基尼系数值，与本文算出的基尼系数大致是吻合的。图1给出了基尼系数随年份的变化趋势。

从图1可以看出1989年至2009年基尼系数的整体变化趋势。虽然从绝对数值上来讲，重庆市城镇居民基尼系数一直在警戒线以下，但我们要看到随着经济发展，城镇基尼系数本身有着不断上升的趋势。目前重庆市城镇基尼系数已由上世纪90年代初期的0.15左右上升到0.27左右，几乎上涨了一倍，因此其带来的影响不可忽略。

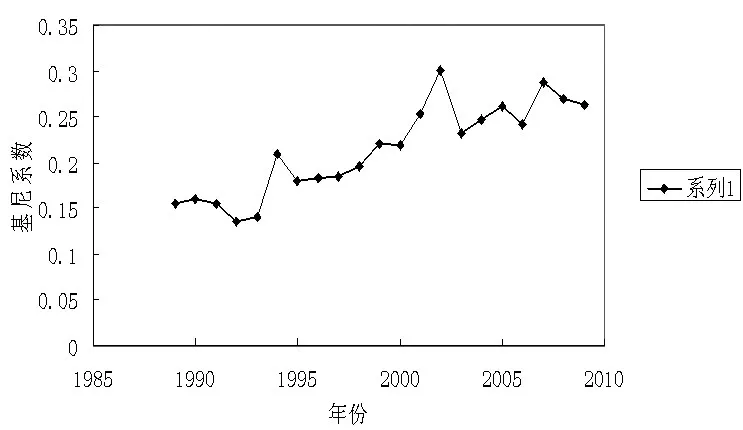
图1 1989年至2009年基尼系数值折线图

图1 中基尼系数变化趋势可分为几个阶段。第一阶段是1989～1993年，这一阶段的特点是基尼系数以上下波动的方式变化，且前后相差不是太大。追溯到统计年鉴中的数据，在上世纪90年代初期城镇居民收入并不高，收入分组数据中显示最高收入分组为180元以上，收入分组组距相差较小。因此我们推断在早期基尼系数维持在一个相对较低且稳定的水平，一方面归因于经济整体发展水平不高，收入水平尚不能拉开较大差距；另一方面则归因于早期相对平均、集中的分配方式。第二阶段是1994～2001年，1994年是一个转折点，首先体现在收入分组方法上，最低收入规定为150元及以下，最高收入户则上升到750元以上，此后的年份在此基础上有一些微调。其次在数值上，1994年基尼系数明显高于其前后的年份，可能与分组方法等因素有关。1995～2001年基尼系数的变化基本呈上升态势，很好地反映了经济发展中收入不平等水平的变化趋势。第三阶段是2002～2009年，2002年在此处又是一个转折点。统计年鉴中说明，由于2002年统计制度的调整，2002年以后的收入分组统计口径与先前的年份有不同，这一原因可能造成了2002年基尼系数明显偏大。同时在考察学者们对其他省份该年份及前后几年城镇基尼系数值后发现各省份城镇基尼系数均在2002年有一个相对畸高的上升。2002年以后，城镇基尼系数变化则是呈现先升后降的趋势，且下降的年份是在2008、2009年。综合上述分析，我们可得出，1989～2009年重庆市城镇基尼系数总体上呈上升趋势，城镇居民收入不平等水平是越来越大，政府有必要重视这一现实。

2.2 倒U曲线拟合实证分析

本研究中经济增长采用人均GDP的对数值作为自变量，即GDP与基尼系数之间的关系是Gini=m(lngdp)。从重庆市统计年鉴采集人均GDP数值并计算对数值。如表2所示。

表2 1989～2009年重庆市城镇居民人均GDP及对数值

在获取模型实证分析所需的数据后，本研究主要通过R软件中运用locpoly命令进行非参数局部多项式回归。非参数局部多项式回归中对于带宽的选择对于估计值的准确性有很大影响，这个部分的实现通过在R软件编程计算得到最佳窗宽为0.513。表3是通过软件进行非参数局部多项式回归的数据结果。

根据前述的倒U曲线非参数局部多项式回归模型，我们要估计的主要参数值即为βj在上表中则为基尼系数估计值，拟合函数的一阶导、二分之一二阶导。二阶偏导数数学含义是，若m′(X0)＜0表示曲线在X0点附近是凸弧，收入分配不平等速度减速上升；若m″(X0)＞0则表示曲线在X0附近是凹弧，收入分配不平等速度加速上升。当m″(X0)=0时，且X0点左右二阶导符号相反，则X0点处为函数的一个拐点。一阶导的数学含义是，若m″(X0)＜0表示在X0处m(X0)有上升的趋势，反之表示m(X0)有下降的趋势。

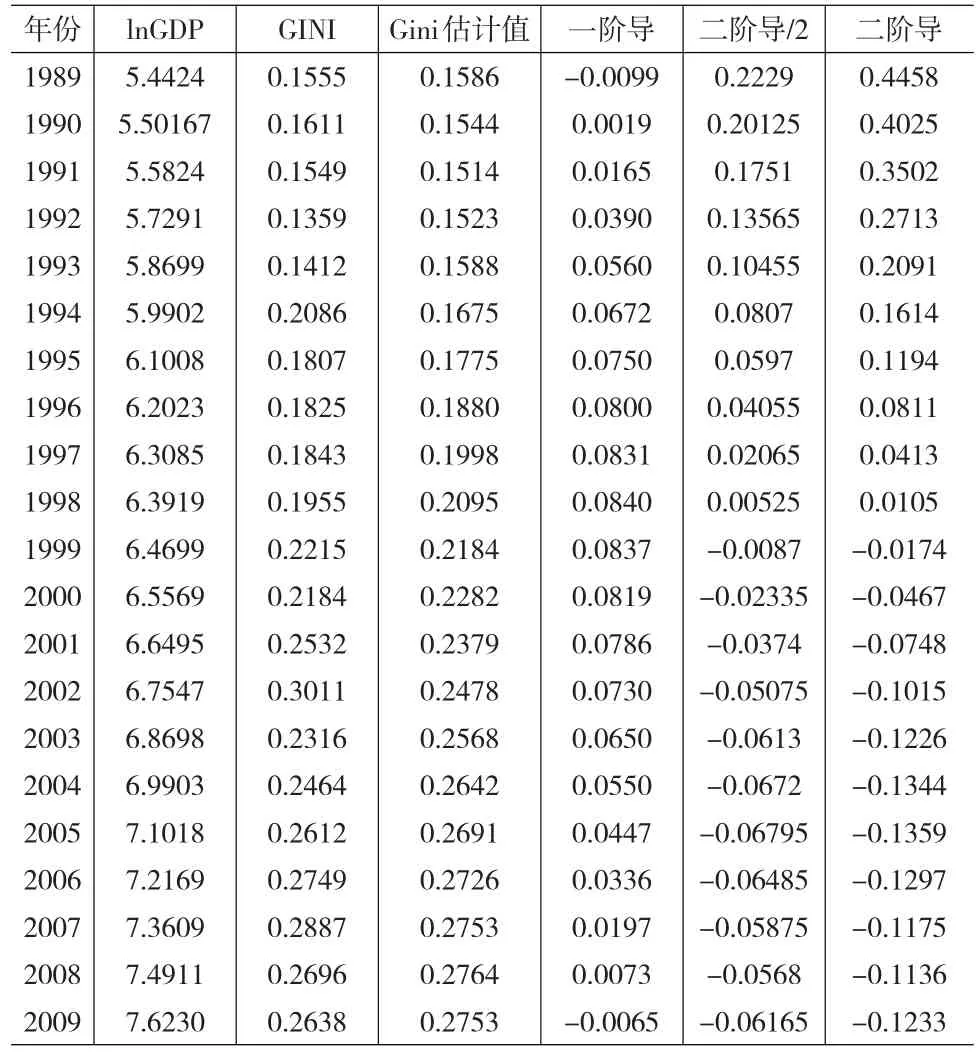
表3 模型数据与主要估计结果

由表3的数据结果我们可以给出倒U曲线图，以方便我们更清晰明了地探讨倒U曲线的发展变化趋势，如图2所示

从图2可以看出，通过R软件进行非参数局部多项式回归拟合后的收入不平等曲线是一条光滑曲线，能够清晰地看出基尼系数与经济增长之间的互动关系。整体上来讲，在1989～2009年间，随着经济水平的提高，重庆城镇基尼系数除在个别年份有回落外主要呈不断上升趋势，显示出重庆城镇收入不平等程度在逐年加深。但同时我们也注意到在图2中，倒U曲线在发展至尾端时已非常平坦，甚至有缓慢下降的趋势。

接下来在本研究中，我们需要寻找倒U曲线的拐点，拐点的含义是倒U曲线在此前后凹凸性发生改变，由此可以探讨在基尼系数不断上升的条件下，其增长速度是怎样变化的。函数拐点出现在二阶导变号，一阶导保持同号的年份前后。由表3我们发现倒U曲线仅存在一个拐点，即在1998、1999年前后倒U曲线的凹凸性发生改变。我们将模型拟合的二阶导结果绘成图3，可清晰看到从1989年到2009年间基尼系数上升态势确实只发生了一次改变。对倒U曲线在重庆城镇地区的实证检验，我们并未得到与学者许冰、章上峰所提出的多拐点过山车式倒U曲线演变趋势。但实证研究结果仍对于研究重庆地区城镇居民收入不平等问题有重要指导意义。

图2 重庆城镇收入不平等曲线变化趋势

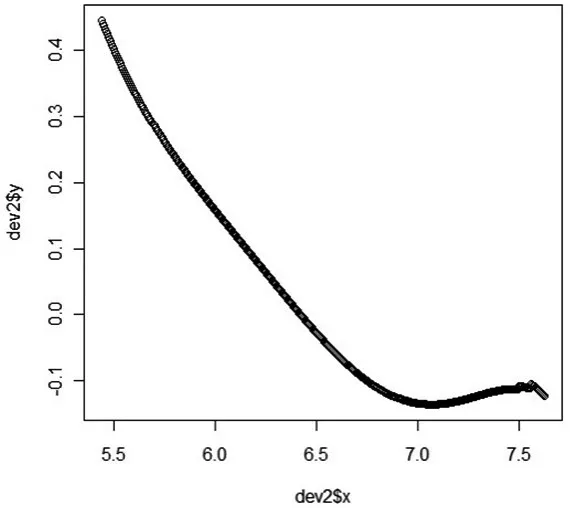
图3 模型拟合二阶导变化曲线

结合图形及数据充分显示，我们可以将重庆城镇收入不平等发展趋势按增长速度简单划分为两个阶段。第一阶段从1989年到1998年，这段时间倒U曲线一阶导与二阶导始终为正，这表明这段时期基尼系数是随社会经济增长不断呈加剧上升的态势，标志着城镇居民收入不平等状况愈演愈烈；第二阶段则是从1999年到2008年，这一阶段倒U曲线面临的是一阶导始终为正而二阶导始终为负的状态，这表明这段期间城镇基尼系数虽然也一直在上升，但其上升速度已有所放缓。同时值得注意的是在2009年倒U曲线的一阶导数已变为负数，这说明倒U曲线必然经历了导数为零的驻点，即倒U曲线已达到了极大值点。

由上述分析可知，重庆城镇人口收入分配不平等状况目前已经过了倒U曲线的左半边，基尼系数的发展趋势目前停留在减速下降的阶段。因此，可以预测倒U曲线未来几年内是以下降的趋势发展，即城镇居民收入差距过大这一现状将会出现不断好转。但对于未来更长时间内城镇人口收入分配不平等状况是否会出现多拐点，是否会有过山车式等复杂的演变趋势，则有赖于更为长期的数据观察才能得出定论。

2.3 倒U曲线发展趋势预测

经过对重庆市城镇居民收入差距进行实证研究，对倒U理论进行了验证。最终结果显示，在经济增长过程中，收入分配不平等水平确实与经济增长之间存在着倒U曲线变化关系，目前重庆城镇收入分配不平等水平已经过倒U曲线的左半部分，走向了倒U曲线的右半边。在1989到2008年间，重庆城镇人口收入不平等程度是逐年上升的，但上升的速度有所区别，而到2009年开始重庆城镇人口收入不平等状况已开始有所好转。虽然目前重庆市城镇人口收入不平等程度是处在减速下降阶段，重庆城镇收入分配不平等程度已达到相当水平，过去二十几年来这种不平等增幅过大。政府和社会对此应高度重视。

虽然从长期看，如果承认倒U曲线的存在，则同时承认了政府干预是无效的，经济发展会自行走出收入分配不平等这一困境，但一个社会对贫富差距有一定的忍耐限度。目前重庆市城镇基尼系数虽然在绝对值上处于国际警戒线之下，但因城镇人口的增多、近年来基尼系数过大的涨幅，城镇基尼系数势必成为整体基尼系数主导因素。城镇居民群体作为现代经济社会的中流砥柱，他们拥有更多的知识水平和社会资源，落实好这部分人的生活问题、安定问题，才能促进和谐社会、城乡统筹的总目标的实现。因此，重庆市政府在把基尼系数纳入政绩考核体系时，不仅应关注现阶段矛盾较大的城乡差距，更要城镇居民收入差距。

3 结语

本文通过非参数局部多项式回归方法对重庆市城镇居民基层系数和人均GDP的关系进行倒U假说验证。总体来说，本文得到以下两点重要结论：

（1）重庆市城镇居民收入不平等状况符合倒U假说，城镇居民收入不平等状况已达到极大值点，但为进一步防止重庆市城镇社会各阶层收入差距进一步恶化和社会不稳定因素出现，政府应予以重视。

（2）重庆市城镇居民收入不平等状况增长趋势确实发生了增速变化，但目前并未出现多拐点过山车式上升的演变趋势。

[1]Kuznets S.Economic Growth and Income Inequality[J].American Eco⁃nomic Review,1955，（45）.

[2]许冰，章上峰.经济增长与收入分配不平等的倒U型多拐点测度研究[J].数量经济技术经济研究，2010,（2）.

[3]李子奈，叶阿忠.高等计量经济学[M].北京：清华大学出版社，2000.

[4]陈昌兵.各地区居民收入基尼系数计算及其非参数计量模型分析[J].数量经济技术经济研究，2007,（1）.

[5]王祖祥.中部六省基尼系数的估算研究[J].中国社会科学，2006,（4）.

[6]李玲慧.外贸出口对中国经济增长影响分析[J].科学决策,2010，(3).