与广义欧拉函数有关的方程

俞洪玲，沈忠燕

(浙江外国语学院科学技术学院，浙江杭州310012)

与广义欧拉函数有关的方程

俞洪玲，沈忠燕*

(浙江外国语学院科学技术学院，浙江杭州310012)

利用初等方法，研究与广义欧拉函数有关的方程φ2(n)=2ω(n)、φ2(φ2(n))= 2ω(n)的可解性，并获得方程的所有正整数解.

广义欧拉函数;方程;正整数解

1 引言

为了将Lehmer同余式从模素数的平方推广到模任意整数的平方，蔡天新［6］等定义了如下的广义欧拉函数.

定义 广义欧拉函数

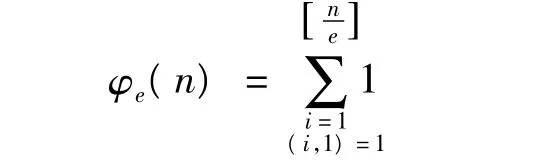
定理1方程的所有正整数解为n=5，8，15，20，24，60.

定理2方程的所有正整数解为n=11，17，25，32，51，55，62，65，68，75，77，80，82，88，93，96，99，100，104，112，122，124，144，165，170，195，204，220，231，238，240，246，260，264，280，286，300，306，308，310，312，336，350，360，366，372，396，450，510，660，714，780，840，858，924，930，990，1050，2310.

2 引理

为了完成定理的证明，我们需要引入一些引理.

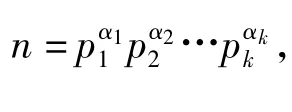
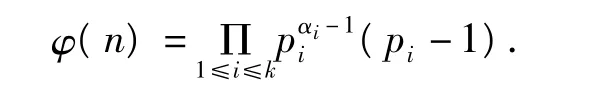
引理2 方程φ2(n)=1的正整数解为n=2，3，4，6.

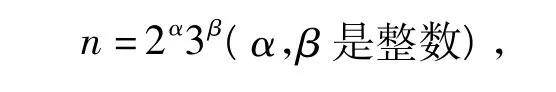
由引理1得

a)当α=β=0时，方程显然无解;

b)当α≠0，β=0时，φ(n)=φ(2α)=2α－1=2，则α=2，即n=4;

c)当α=0，β≠0时，φ(n)=φ(3β)=3β－12=2，则β=1，即n=3;

d)当α≠0，β≠0时，φ(n)=φ(2α3β)=2α－13β－12=2，则α=β=1，即n=6.

综上可得，方程φ2(n)=1的正整数解为n=2，3，4，6.

引理3 方程φ2(n)=2的正整数解为n=5，8，10，12.

证明 由φ2(n)=φ(n)得φ(n)=4，则n的素因数小于等于5，令

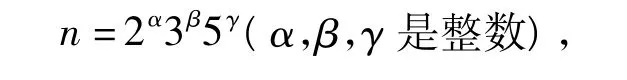
由引理1得

a)当α=β=0，γ≠0时，φ(n)=φ(5γ)=5γ－14=4，则γ=1，即n=5; b)当γ=β=0，α≠0时，φ(n)=φ(2α)=2α－1=4，则α=3，即n=8; c)当β≠0，α=γ=0时，φ(n)=φ(3β)=3β－12=4，方程显然无解;

d)当γ=0，α≠0，β≠0时，φ(n)=φ(2α3β)=2α－13β－12=4，则α=2，β=1，即n=12; e)当β=0，α≠0，γ≠0时，φ(n)=φ(2α5γ)=2α－15γ－14=4，则α=γ=1，即n=10;

f)当α=0，β≠0，γ≠0时，φ(n)=φ(3β5γ)=3β－15γ－18=4，方程显然无解;

g)当α=β=γ=0时，方程显然无解;

h)当α≠0，β≠0，γ≠0时，φ(n)=φ(2α3β5γ)=2α－13β－15γ－18=4，方程显然无解.综上可得，方程φ2(n)=2的正整数解为n=5，8，10，12.

引理4 方程φ2(n)=4的正整数解为n=15，16，20，24，30.

证明 由φ2(n)=4可知φ(n)=8，则n的素因数小于等于5，令

用引理3的方法可得方程φ2(n)=4的正整数解为n=15，16，20，24，30.

引理5 方程φ2(n)=8的正整数解为n=17，32，34，40，48，60.

证明 由φ2(n)=8可知φ(n)=16，则n的素因数小于等于17，由16的因子可以令

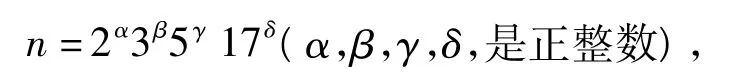
用引理3的方法可得方程φ2(n)=8的正整数解为n=17，32，34，40，48，60.

引理6 方程φ2(n)=16的正整数解为n=51，64，68，80，96，102，120.

证明 由φ2(n)=16可知φ(n)=32，则n的素因数小于等于17，由32的因子可以令

用引理3的方法可得方程φ2(n)=16的正整数解为n=51，64，68，80，96，102，120.

引理7 方程φ2(n)=5的正整数解为n=11，22.

证明 由φ2(n)=5可知φ(n)=10，则n的素因数小于等于11，由10的因子可以令

用引理3的方法可得方程φ2(n)=5的正整数解为n=11，22.

引理8 方程φ2(n)=10的正整数解为n=25，33，44，50，66.

证明 由φ2(n)=10可知φ(n)=20，则n的素因数小于等于19，由20的因子可以令

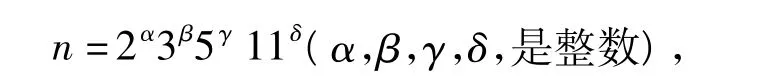
用引理3的方法可得n=25，33，44，50，66.

引理9 方程φ2(n)=12的正整数解为n=35，39，45，52，56，70，72，78，84，90.

证明 由φ2(n)=12可知φ(n)=24，则n的素因数小于等于13，由24的因子可以令

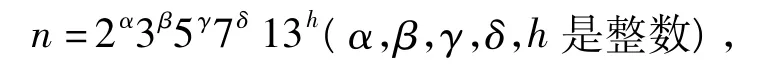
用引理3的方法可得n=35，39，45，52，56，70，72，78，84，90.

引理10 方程φ2(n)=17无解.

证明 由φ2(n)=17可知φ(n)=34，则n的素因数小于等于17，由34的因子可以令

用引理3的方法可知n无解.

引理11 方程φ2(n)=15的解为n=31，62.

证明 由φ2(n)=15可知φ(n)=30，则n的素因数小于等于31，由30的因子可以令

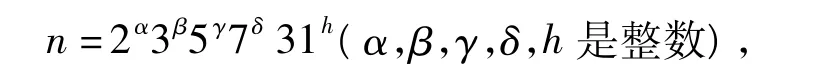
用引理3的方法可知n=31，62.

引理12 方程φ2(n)=20的解为n=41，55，75，82，88，100，110，132，150.

证明 由φ2(n)=20可知φ(n)=40，则n的素因数小于等于41，由40的因子可以令

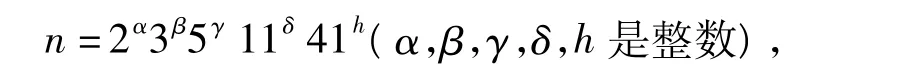
用引理3的方法可知n=41，55，75，82，88，100，110，132，150.

引理13［7］53当n为正奇数时，φ(2n)=φ(n);当n为正偶数时，φ(2n)=2φ(n).

引理14 φ2(n)=24的解为n=65，104，105，112，130，140，144，156，168，180，210.φ2(n)=30的解为n=61，77，93，99，122，124，154，186，198.φ2(n)=32的解为n=85，128，136，160，170，192，204，240.

证明类似于引理3.

3 定理1的证明

n=1，n=2显然都不是方程φ2(n)=2ω(n)的解.下面讨论n＞2时，方程φ2(n)=2ω(n)解的情况.

3.1 当ω(n)=1时

当ω(n)=1时，由引理3可知满足φ2(n)=2的解为n=5，8，10，12.这些解中满足ω(n)=1的解为n=5，8.

3.2 当ω(n)=2时

当ω(n)=2时，φ2(n)=4，由引理4可知满足φ2(n)=4的解为n=15，16，20，24，30.这些解中满足ω(n)=2的解为n=15，20，24.

3.3 当ω(n)=3时

当ω(n)=3时，φ2(n)=8，由引理5可知满足φ2(n)=8的解为n=17，32，34，40，48，60.这些解中满足ω(n)=3的解为n=60.

3.4 当ω(n)≥4时

令n=pα11pα22…pαkk(k≥4)，其中p1，p2，…，pk为不同素数，满足2≤p1＜p2＜…＜pk，

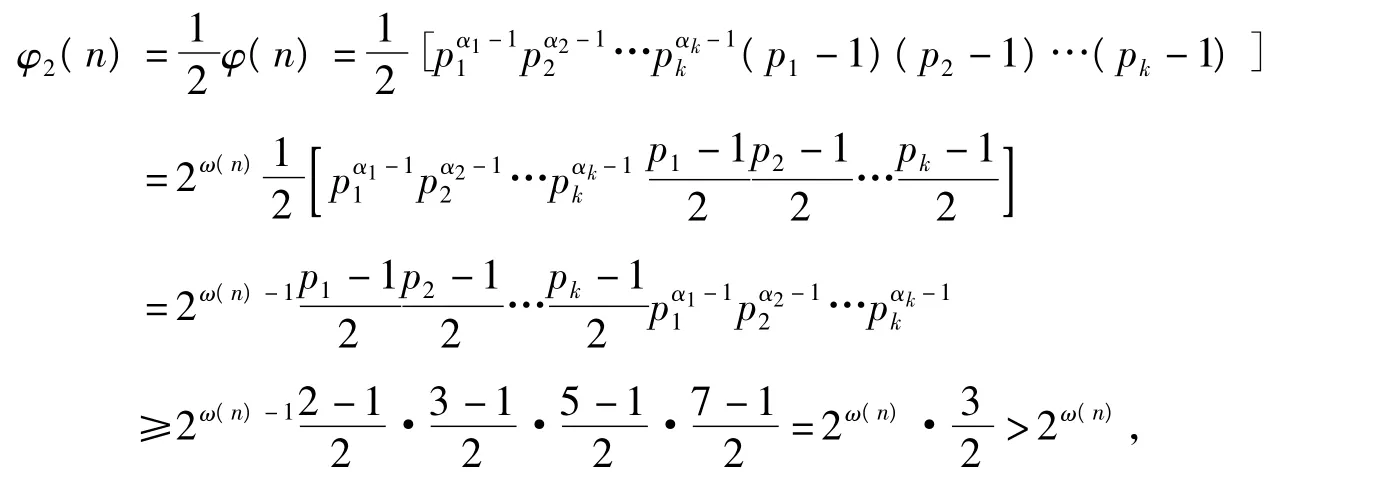
所以当ω(n)≥4时，方程φ2(n)=2ω(n)无解.综上可知，方程(1)仅有6个解n=5，8，15，20，24，60.

4 定理2的证明

由广义欧拉函数定义及引理2，引理3可知n=1，2，3，4，5，6，7，8，9，10，12都不是方程φ2(φ2(n)) =2ω(n)的解.容易验证n=11是方程φ2(φ2(n))=2ω(n)的其中一个解.下面讨论n＞12(即φ2(n)＞2)，方程φ2(φ2(n))=2ω(n)解的情况.

4.1 当ω(n)=1时

当ω(n)=1时，φ2(φ2(n))=2，由引理3可知，φ2(n)=5，8，10，12.

4.1.1 当φ2(n)=5时，n的取值情况

当φ2(n)=5时，由引理7可知，n=11，22.这些解中满足ω(n)=1的解为n=11.

4.1.2 当φ2(n)=8时，n的取值情况

当φ2(n)=8时，由引理5可知，n=17，32，34，40，48，60.这些解中满足ω(n)=1的解为n= 17，32.

4.1.3 当φ2(n)=10时，n的取值情况

当φ2(n)=10时，由引理8可知，n=25，33，44，50，66.这些解中满足ω(n)=1的解为n=25.

4.1.4 当φ2(n)=12时，n的取值情况

当φ2(n)=12时，由引理9可知，n=35，39，45，52，56，70，72，78，84，90.这些解中不存在满足ω (n)=1的解.

4.2 当ω(n)=2时

当ω(n)=2时，φ2(φ2(n))=4，由引理4可知，φ2(n)=15，16，20，24，30.

4.2.1 当φ2(n)=15时，n的取值情况

当φ2(n)=15时，由引理11可知，n=31，62.这些解中满足ω(n)=2的解为n=62.

4.2.2 当φ2(n)=16时，n的取值情况

当φ2(n)=16时，引理6可知，n=51，64，68，80，96，102，120.这些解中满足ω(n)=2的解为n= 51，68，80，96.

4.2.3 当φ2(n)=20时，n的取值情况

当φ2(n)=20时，由引理12可知，n=41，55，75，82，88，100，110，132，150.这些解中满足ω(n)= 2的解为n=55，75，82，88，100.

4.2.4 当φ2(n)=24时，n的取值情况

当φ2(n)=24时，引理14可知，n=65，104，105，112，130，140，144，156，168，180，210.这些解中满足ω(n)=2的解为n=65，104，112，144.

4.2.5 当φ2(n)=30时，n的取值情况

当φ2(n)=30时，由引理14可知，n=61，77，93，99，122，124，154，186，198.这些解中满足φ(n) =2的解为n=77，93，99，122，124.

4.3 当ω(n)=3时

当ω(n)=3时，φ2(φ2(n))=8，由引理5可知，φ2(n)=17，32，34，40，48，60.所以，φ(n)=34，64，68，80，96，120.令

其中p1，p2，p3为不同素数，由引理1可知，

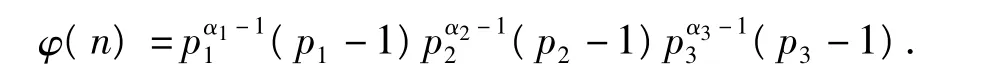
4.3.1 当φ(n)=34时，n的取值情况

当φ(n)=34时，

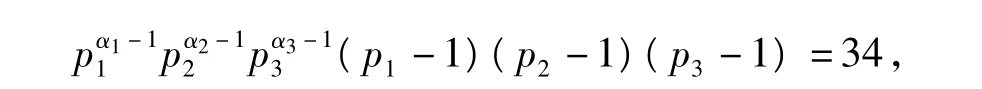
由计算可知没有满足条件的n值.

4.3.2 当φ(n)=64时，n的取值情况

当φ(n)=64时，

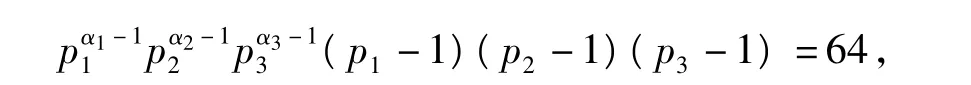
由计算可知满足条件的n=170，204，240.

4.3.3 当φ(n)=68时，n的取值情况

当φ(n)=68时，

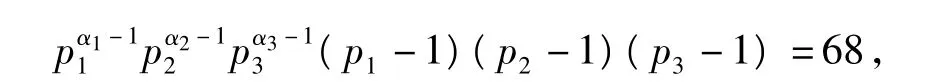
由计算可知没有满足条件的n值.

4.3.4 当φ(n)=80时，n的取值情况

当φ(n)=80时，

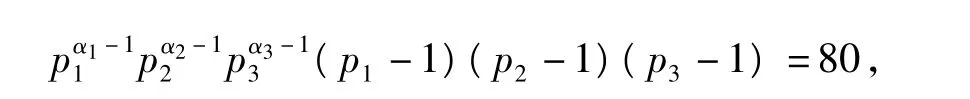
由计算可知满足条件的解为n=165，220，246，264，300.

4.3.5 当φ(n)=96时，n的取值情况

当φ(n)=96时，

由计算可知满足条件的解为n=195，238，260，280，306，312，336，360.

4.3.6 当φ(n)=120时，n的取值情况

当φ(n)=120时，

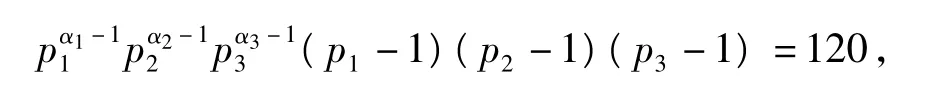
由计算可知满足条件的解为n=231，308，310，350，366，372，396，450.

4.4 当ω(n)=4时

当ω(n)=4时，φ2(φ2(n))=16，引理6可知，φ2(n)=51，64，68，80，96，102，120.所以，φ(n)= 102，128，136，160，192，204，240.令

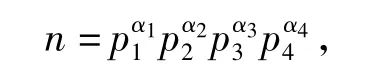
其中p1，p2，p3，p4为不同的素数.由引理1可知，

4.4.1 当φ(n)=102时，n的取值情况

当φ(n)=102时，

由计算可知没有满足条件的解.

4.4.2 当φ(n)=128时，n的取值情况

当φ(n)=128时，

由计算可知满足条件的解为n=510.

4.4.3 当φ(n)=136时，n的取值情况

当φ(n)=136时，

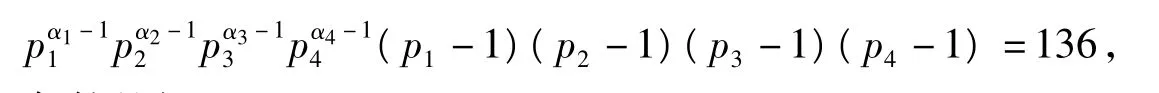
由计算可知没有满足条件的解.

4.4.4 当φ(n)=160时，n的取值情况

当φ(n)=160时，

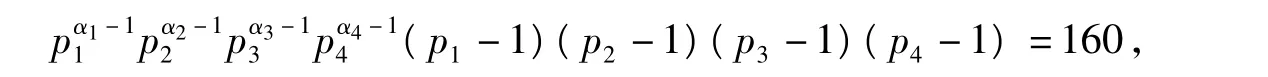
由计算可知满足条件的解为n=660.

4.4.5 当φ(n)=192时，n的取值情况

当φ(n)=192时，

由计算可知满足条件的解为n=714，780，840.

4.4.6 当φ(n)=204时，n的取值情况

当φ(n)=204时，

由计算可知没有满足条件的解.

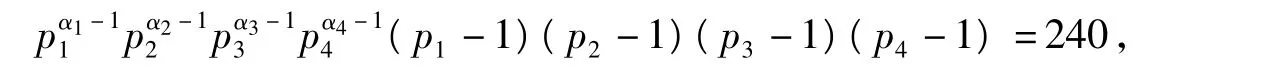
4.4.7 当φ(n)=240时，n的取值情况当φ(n)=240时，由计算可知满足条件的解为n=858，924，930，990，1050.

4.5 当ω(n)=5时

当ω(n)=5时，φ2(φ2(n))=32，引理14可知，φ2(n)=32的解为n=85，128，136，160，170，192，204，240.所以，

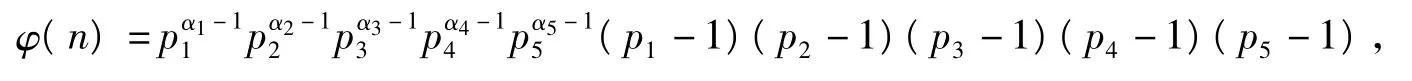
当p1，p2，p3，p4，p5取最小的5个素数时，由计算可知

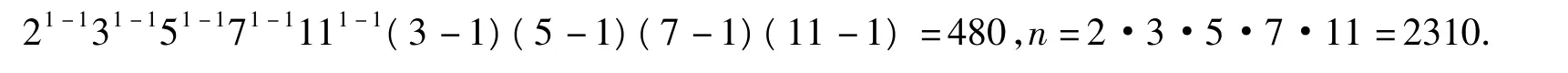
所以当ω(n)=5时，只有n=2310一个解.

4.6 ω(n)≥6时

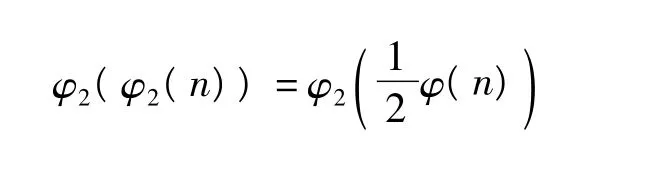
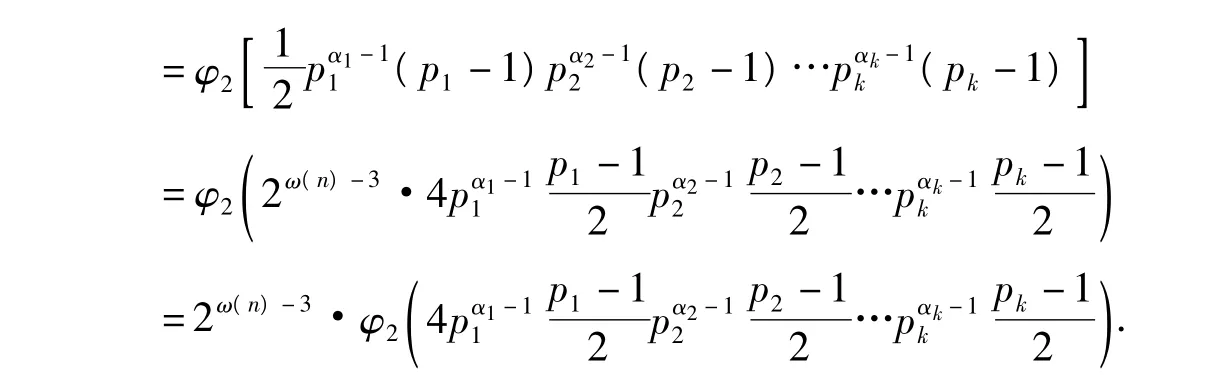
故方程φ2(φ2(n))=2ω(n)等价于

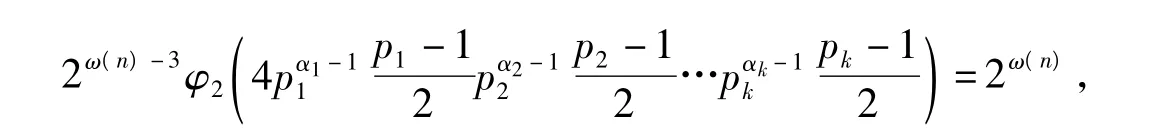
所以要求解方程φ2(φ2(n))=2ω(n)的解，只需求解方程

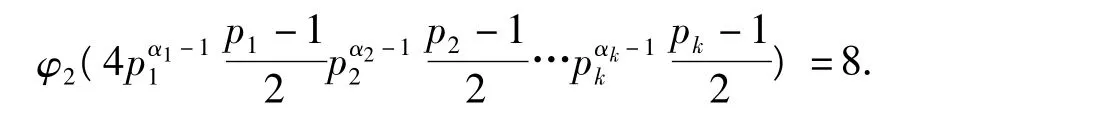
由引理5可知，方程φ2(n)=8的解为n=17，32，34，40，48，60.则只需求解方程

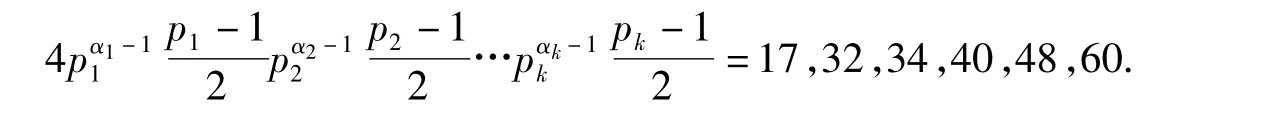
因为

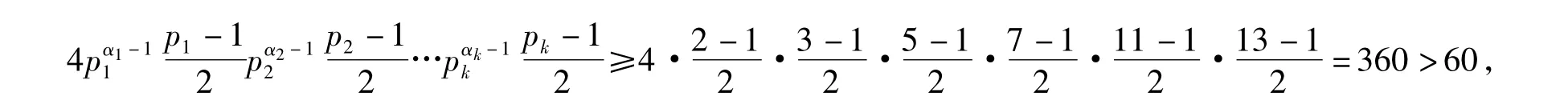
所以当ω(n)≥6时，方程φ2(φ2(n))=2ω(n)无解.综上可知，方程(2)的解为n=11，17，25，32，51，55，62，65，68，75，77，80，82，88，93，96，99，100，104，112，122，124，144，165，170，195，204，220，231，238，240，246，260，264，280，286，300，306，308，310，312，336，350，360，366，372，396，450，510，660，714，780，840，858，924，930，990，1050，2310.

［1］吕志宏.一个包含Euler函数的方程［J］.西北大学学报:自然科学版，2006，36(1):17-20.

［2］马静.方程φ(n)=2tw(n)(t∈Z+)的解［J］.安徽师范大学学报:自然科学版，2009，32(1):23-26.

［3］Zhang T P，Ma Y K.An equation involving Euler’s φ function［J］.Scientia Magna，2008，4(1):109-112.

［4］田呈亮.一个包含欧拉函数的方程［J］.纯粹数学与应用数学，2006，26(1):96-98.

［5］李怡君.一类数论函数的性质［J］.商丘师范学院学报，2007，23(9):20-22.

［6］Cai T X，Fu X D，Zhou X.A congruence involving the quotients of Euler and its applications(II)［J］.Acta Arith，2007，130(3):203-214.

［7］Hardy G H，Wright E M.An Introduction to the Theory of Numbers［M］.北京:人民邮电出版社，2007.

The Equations Related with Generalized Euler Function

YU Hongling，SHEN Zhongyan
(School of Science and Technology，Zhejiang International Studies University，Hangzhou 310012，China)

The equations φ2(n)=2ω(n)and φ2(φ2(n))=2ω(n)related with generalized Euler function is studied using elementary method，and all positive integer solutions are obtained.

generalized Euler function;equation;positive integer solutions

O156.4

A

2095－2074(2012)03－0091－07

2012－03－01

俞洪玲(1990－)，女，浙江杭州人，浙江外国语学院科学技术学院数学系数学与应用数学专业2008级本科生.

*通讯作者:沈忠燕(1978－)，女，浙江桐乡人，浙江外国语学院科学技术学院数学系讲师，理学博士.