空间快速响应航天器轨道/弹道一体化规划①
黄文博,张 强,肖 飞,张为华
(1.国防科技大学航天与材料工程学院,长沙 410073;2.陆军航空兵学院,北京 101123)
0 引言
空间快速响应[1]是指发生战争或自然灾害等突发事件时,运载系统能够在短时间内实现机动、完成测试并发射,当有效载荷入轨后能马上执行预定任务,而不需经过长时间的在轨调整[2]。针对突发事件,运载器需要满足“机动性”和“快速性”的要求,与液体火箭比较,小型固体运载器更适合作为“空间快速响应”任务的发射工具。
当前航天器飞行轨迹规划的研究主要分为轨道规划[3]和弹道规划[4-5]两部分。通常轨道规划任务主要完成轨道要素的设计,弹道规划将轨道要素作为终端约束,选择发射点和发射时刻,并设计从发射点到入轨点的飞行弹道,轨道规划和弹道规划需进行反复迭代最终完成规划任务。“空间快速响应”的特点是任务具有不确定性,轨道参数与发射诸元参数需在接到任务后进行规划设计,要求轨道/弹道规划设计的时间越短越好。如果采用传统设计方法,规划迭代时间较长,势必影响其“快速性”。因此,将轨道/弹道作为一个整体进行优化设计是实现快速性的有效方法。由于设计参数多,单一优化算法很难对此复杂问题进行优化。近年来,改进的智能优化算法在飞行器轨迹优化设计[6-7]领域得到应用,混合优化方法[8]和分级规划策略[9-10]由于综合收敛性好,也在轨迹优化中得到迅速发展。
本文从任务需求出发,使用分级规划策略,采用改进的粒子群算法和牛顿迭代算法,将空间快速响应航天器轨道、弹道进行一体化混合优化求解。最终实现轨道/弹道一体化快速规划设计。
1 数学模型
1.1 轨道规划
空间快速响应的一个重要任务为对地观察,为满足可见光照相侦察任务需求,有效载荷经过目标区域的光照条件应基本一样,另考虑到重访的需求,星下点轨迹还应周期性重复,故目标轨道应该选择圆形太阳同步回归轨道。对这种近圆轨道,近地点不确定,可采用如下轨道要素描述:半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、纬度幅角u(由于太阳同步轨道不会出现i=0°或 i=180°,因此此处不涉及赤道轨道的特例)。轨道规划即是确定以上除e以外的4个参数。
(1)半长轴
圆轨道半长轴由轨道高度h决定。对采用可见光的有效载荷,限制轨道高度的因素主要有成像分辨率、测控、轨道寿命、安全性和回归性等。
(2)轨道倾角
在J2项摄动下,利用太阳同步轨道的轨道面进动角速率与平太阳在赤道上移动的角速度相等的特点,确定轨道倾角i。
(3)升交点赤经与纬度幅角
纬度幅角u决定有效载荷在轨道面内的位置,任务规划时按光照条件需求,规划星下点轨迹过目标点的当地时。参见图 1,λtgt、φtgt为目标点经纬度,在由u0、φtgt和λ0构成的球面直角三角形中有如下关系式:
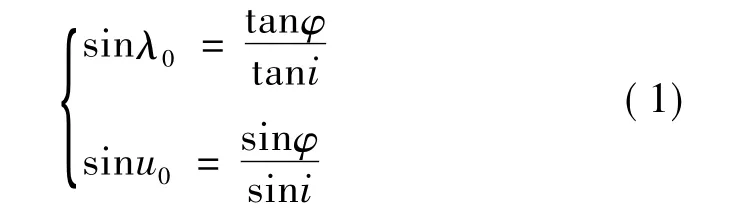

由式(1)可求出λ0和u0,进而求得Ω:
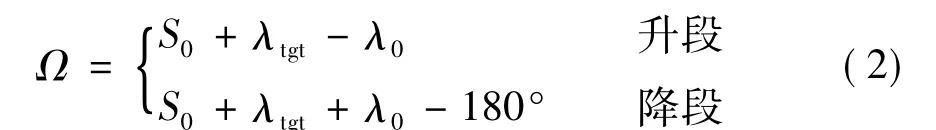
式中 S0为当前时刻零经度线到真春分点的角距。
需说明的是升交点赤经设计除了考虑轨道过目标的升降关系,还要综合考虑轨道过目标点的地方时、目标区域的光照情况、太阳高度角及卫星对目标区域的覆盖情况。详细设计过程参见文献[3]。
1.2 弹道规划
本文研究的运载器由三级固体发动机和液体末助推级组成。运载器采用直接入轨方式,飞行弹道分为7段:一级动力飞行段、一级滑行段、二级动力飞行段、二级滑行段、三级动力飞行段、三级滑行段、四级末助推段。运载火箭俯仰程序角设计与参考文献[6]类似,不同之处有:
(1)一级飞行段负攻角转弯段
俯仰角设计采用文献[11]中三角函数型飞行程序角:

式中 t1为垂直起飞结束时刻;t2为负攻角转弯结束时刻。
(2)一级、二级滑行段
滑行段结束不以飞行时间t而以当前飞行高度作为判断准则,以一级滑行段为例,程序角设计为
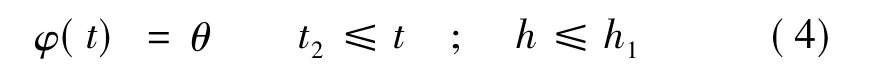
其中,h1为一级滑行结束高度。仿真中使用simulink自带的stateflow工具,来实现飞行时间t和飞行高度h的综合逻辑判断。
程序角设计变量有:
式中 tmax为最大攻角出现时刻;αm为攻角绝对值最大值;˙φi(i=2,3,4)为各级动力飞行段俯仰角变化率;h2为二级滑行结束高度;tc3为三级滑行时间;t4为末助推级飞行时间。
每一组状态X对应一条运载段弹道,弹道规划过程即是变量X的优化求解过程。
2 算法设计
2.1 数学模型求解过程分析
弹道规划是进行飞行程序角参数X、发射方位角A、发射点经纬度(λlch,φlch)和发射时刻 t0的设计优化,以使有效载荷能在适当的时刻进入预定轨道,并使轨道调整时间尽量少。由轨道设计知,A、(λlch,φlch)和t0的初值由有效载荷星下点轨迹决定,给定X初值进行弹道积分,就可计算出实际入轨轨道要素,通过实际轨道要素与期望轨道要素的比较结果,对设计参数进行迭代计算或寻优搜索,得到满足入轨条件的弹道设计参数。按照物理意义的不同,轨道要素可分为3类:一是决定轨道形状及大小的a、e;二是决定轨道在惯性空间方位的i、Ω;三是决定当前时刻有效载荷在轨道上位置的u。将上升段弹道近似认为在发射平面内飞行,则a和e由飞行程序角参数X决定;i、Ω和u由发射诸元A、(λ0,φ0)和t0共同决定,弹道规划参数对轨道要素的影响如图2所示,粗线表示影响较大,细实线表示影响较小。对于不同的轨道任务,a和e的变化比较大,X的优化值与设计初值一般相差较大;而发射诸元优化值与由轨道规划得到的诸元初值相差较小。若在优化时采取分级规划优化策略,将2类参数使用粒度不同的优化方法,可提高优化的效率。

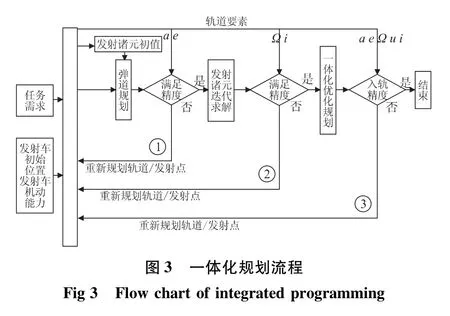
2.2 分级规划优化模型
采用分级规划的思想,将航天器轨道/弹道一体化规划主要分为3个层次(分别对应图3中从里到外3个回路):弹道规划(求解满足入轨轨道高度、偏心率要求的弹道参数)、发射诸元迭代求解(在上一层次规划结果基础上设计发射方位角,发射时刻等)、轨道/弹道一体化规划(在上一层次基础上进行轨道/弹道一体化优化设计,对上2层次设计结果进行微小调整,得到轨道、弹道所有参数优化结果)。
分级规划优化步骤如下:
(1)由任务需求(如对目标最短观测时间、最早发射时间等)和发射点初始位置及发射车机动能力,对期望轨道进行规划,设计期望轨道的轨道要素。
(2)利用轨道倾角、升交点赤经为终端约束条件,计算运载器发射方位角和发射时刻初始值。
(3)以轨道高度、轨道偏心率为终端约束条件,优化计算弹道规划参数,如优化结果无解,转到(1),重新调整期望轨道要素;否则继续。
(4)以轨道倾角、升交点赤经为终端约束条件,以(3)计算结果进行发射方位角和发射时刻精确计算,如满足精度要求,转到(5);否则转到(1)。
(5)以所有轨道要素作为终端约束条件进行优化求解,如优化结果不满足入轨精度要求,转到(1);否则,转到(6)。
(6)结束。
一体化规划中最重要环节分别为轨道规划、弹道规划、发射诸元迭代求解和一体化优化规划,以下对各环节优化方法进行说明。
2.2.1 弹道规划
(1)约束条件。运载器弹道设计优化的约束条件包括终端约束和路径约束。
(2)终端约束
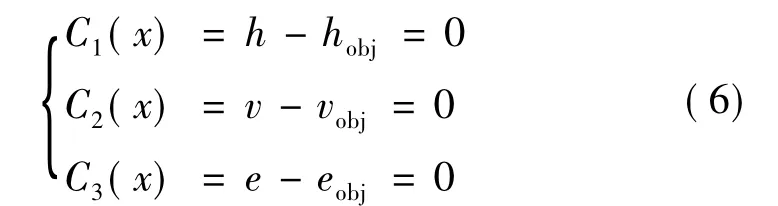
式中 h、v、e分别为实际入轨高度、入轨速度和偏心率,带obj下标的参数分别为目标轨道相应参数。
(3)路径约束

式中 nx、ny、q和qα分别为轴向过载、法向过载、动压和动压与攻角乘积,带max下标的参数分别为相应参数的最大限定值。
(4)目标函数。运载器前三级固体发动机均采用耗尽关机工作模式,末助推级液体推进剂除了用于入轨段修正外,剩余推进剂还为有效载荷提供轨道维持和轨道机动的能量。因此,以末助推发动机工作时间最小为目标函数,即

(5)优化方法。粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法。标准PSO存在不能自适应平衡全局搜索和局部搜索性能,易陷入局部最优、搜索精度不高等问题[6]。因此,弹道优化问题需对标准粒子群算法进行适当改进,如文献[7]引入动态初始化策略对PSO进行改进。惯性权重ω是粒子群优化算法的关键参数,用来平衡粒子的全局和局部搜索能力,较大的惯性权重可使粒子具有较好的探索能力,而较小的惯性权重则可使粒子具有较好的开发能力。优化初始阶段偏向于探索能力,后期偏向于开发能力。因此,本文对惯性权重进行动态调节,以增强其自适应寻优能力。
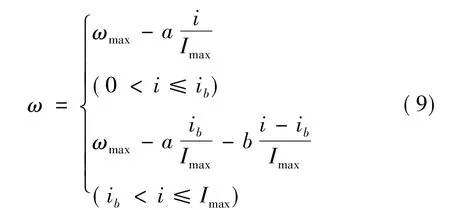
式中 i为当前迭代次数;Imax为最大迭代次数;ib为控制惯性权重衰减率发生变化的节点迭代次数;a、b分别为惯性权重在各阶段的衰减率。
(6)发射诸元迭代求解。发射方位角和发射时刻优化问题为非线性方程的优化求解问题。在求解非线性方程的迭代方法中,牛顿迭代法收敛速度较快,因此选用牛顿迭代法进行求解[4]。
(7)初值。运载器采用机动发射方式,最大机动速度为vmax,最远机动距离为dmax。由轨道要素生成轨道星下点轨迹,以发射车初始位置为圆心,dmax为半径形成机动区域边界圆,包含在边界圆内且满足任务时间的星下点轨迹为可发射段。选可发射段上离初始点最近的点(λlch,φlch)为发射点,发射方位角A由轨道倾角i和发射点纬度φlch计算求得;发射时刻t0选为卫星过发射点时刻。
(8)迭代过程。以发射方位角A求解为例,以入轨点轨道倾角i为目标量,设目标弹道倾角为i*,A按下述步骤确定:
1)令迭代次数控制变量k=0,给定A初值A0和迭代计算控制精度ε;
2)进行弹道积分计算,得到入轨点轨道倾角ik,判断是否有|ik-i*|<ε,若是,转步骤5),否则转下一步;

4)根据牛顿迭代公式:
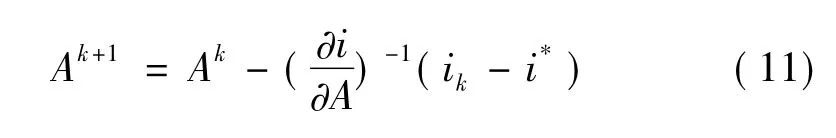
令k=k+1,跳至步骤(2);
5)结束运算,输出计算结果。
发射方位角t0求解过程类似,只是目标量为入轨点纬度幅角u。
(9)轨道/弹道一体化混合优化。严格说来,每一个弹道规划参数对任意一个轨道要素均有影响,通过以上优化,得到除发射点经纬度外较优化的弹道设计参数。可知此时的设计参数在设计变量空间中离最优值已经“很近”,再通过粒子群优化算法进行优化,得到综合最优参数。此时的优化设计变量X:
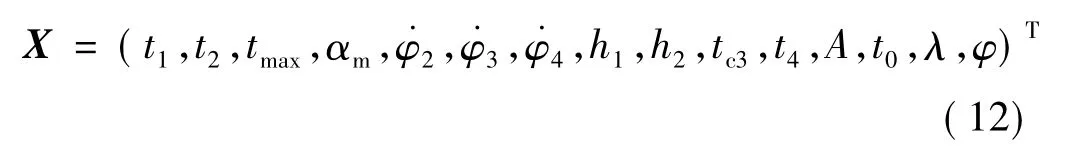
(10)终端约束变成为

路径约束仍为式(7)。
综合优化结果即为轨道/弹道一体化优化参数,运载器按照优化弹道参数及发射诸元发射入轨,能在第1圈即进入预定轨道实现轨道任务。
3 算例及结果
(1)任务背景
北京时间2010年4月14日7时49分,青海省玉树地区(N33.05°,E96.85°)发生 7.1 级地震,造成重大伤亡,由于地理位置原因,没有合适的在轨卫星覆盖此地区,为掌握第一手震区资料,需要1颗成像卫星对玉树地区形成每日观察能力。
(2)任务需求
2010年4 月15日,开始形成对玉树地区的观察能力,卫星过目标地区当地时要求:8:00~17:00。
(3)初始条件
发射车初始发射车位置:湖南长沙(N28.19°,E112.97°);
发射车机动能力:vmax=60 km/h,dmax=600 km;
接收命令时间:北京时间2010年4月14日12时。
3.1 轨道规划
将地方时转换为世界时(Universal Time,UT),卫星第1次过目标地区时间需求:15 Apr 2010 02:00:00.00 UT ~ 15 Apr 2010 11:00:00.00 UT
接收命令时间:14 Apr 2010 04:00:00.00 UT
按照轨道规划方法,目标轨道为星下点轨迹过玉树地区的太阳同步圆形轨道,轨道要素如表1所示。

表1 规划轨道要素Table 1 The designed orbit elements
3.2 发射诸元初值
以轨道要素形成星下点轨迹,选择运载器机动区域内离发射点最近的点作为发射点,如图4所示。

发射诸元初始值:经纬度(N26.28°,E117.97°),发射方位角 -172.69°,发射时刻15 Apr 2010 01:32:00 UT。通过计算知,机动距离为512 km,假设机动所需时间为7 h,规划优化计算2 h,测试、发射准备4 h,则发射车可在14 Apr 2010 17:00:00.00 UT达到发射点,并进入待发射状态,早于发射窗口的发射时间15 Apr 2010 01:32:00 UT,满足发射时间要求。
3.3 一体化规划优化结果
目标轨道部分设计参数及约束如表2所示。粒子群算法种群规模取为40,进化代数选为100,惯性权重最大值取0.9,最小值取 0.2,学习因子最大值为 2.5,最小值为0.5。初值取范围内的随机值,程序角设计变量和优化设计结果见表2。
发射诸元初值及迭代结果如表3所示。发射诸元只迭代5次就收敛到最优值。
计算结果表明,各项约束条件均得到较好满足。由表4可知,采用轨道/弹道一体化规划设计的参数能达到任务需求。

表3 发射诸元迭代发射数据Table 3 Fire data of Newton iterative method

表4 入轨参数优化结果和约束值Table 4 Orbit elements corresponding to optimal solution
4 结论
(1)采用基于分级策略的航天器轨道/弹道一体化规划,比传统轨道规划完成后再进行弹道规划的方式设计效率更高,设计时间更少。主要原因是本文所采用迭代过程是在一个一体化的程序内部进行,而传统设计方法迭代过程是在相对独立的2个优化程序之间通过人工方式进行。
(2)将弹道规划参数区分为程序角设计参数和发射诸元参数,由于2类参数的性质不同分别采用改进粒子群算法和牛顿迭代算法进行优化求解(避免了单一优化算法对不同优化参数权重分配困难的问题),优化算法收敛速度快,只需几次迭代就能获得最优解,有利于工程实现。
(3)采用一体化规划得到的飞行轨迹能满足快速响应任务精度要求,且减少了运载器入轨后,进行的轨道调整时间,使有效载荷入轨后,飞行第1圈即可执行预定任务。
[1]才满瑞,曲晶.国外航天运输系统发展战略和趋势分析[J].中国航天,2009(2):21-26.
[2]Simon P W,Randall R C.Responsive space and strategic information[J].Defense Horizons,2004,40:1-8.
[3]郗晓宁,王威.近地航天器轨道基础[M].长沙:国防科技大学出版社,2003.
[4]杨希祥,江振宇,张为华.固体运载火箭上升段弹道快速设计方法研究[J].宇航学报,2010,31(4):993-997.
[5]李绿萍,南树军,李卿.FY-2C星发射轨道计算与分析[J].上海航天,2005:12-15.
[6]杨希祥,江振宇,张为华.基于粒子群算法的固体运载火箭上升段弹道优化设计研究[J].宇航学报,2010,31(5):1304-1309.
[7]郭杰,唐胜景,李响,等.基于改进粒子群算法的方案飞行弹道优化设计[J].北京理工大学学报.2010,30(6):688-692.
[8]张洪波,郑伟,汤国建.混合遗传算法在远程交会轨道设计中的应用[J].航天控制,2006,24(2):34-37.
[9]罗亚中,唐国金,梁彦刚,等.GTO发射轨道的两级分解全局优化设计策略[J].中国空间科学技术,2004(4):36-46.
[10]罗亚中,唐国金,梁彦刚.基于分解策略的SSO发射轨道遗传全局优化设计[J].航空学报,2004,25(5):443-446.
[11]杨希祥,江振宇,张为华.小型运载火箭大气层飞行段飞行程序设计研究[J].飞行力学,2010,28(4):68-72.

