基于固体微推力器阵列的卫星控制一体化算法①

刘旭辉，方蜀州，马红鹏，高庆丰

(北京理工大学 宇航学院，北京 100081)

0 引言

“小卫星”是20世纪90年代以后在航天领域广泛应用的新概念。特别是近年来通过应用MEMS技术，使小卫星的体积和质量进一步缩小，向公斤级的皮卫星和纳卫星方向发展。然而，现在国际上研制的微型卫星几乎都不配备推进系统，或只有极其有限的机动能力。而微型固体推进器阵列，由于具有体积小、成本低、功耗低、可靠性高等优点，受到了广泛重视［1－4］，各国展开了将其用于皮纳卫星姿轨控方面的研究，但大部分研究集中于结构设计、微推力测试等。

现阶段对于基于微型推力器阵列的推力器分配算法研究国内外处于空白，而基于液体推力器的分配算法国外有较多研究［5－6］，但姿轨控推力器数量远小于微型推力器阵列。因此，其分配算法不适于基于微型推力器阵列的控制，需设计一种适用于该阵列的推力器分配算法，才能使推力器阵列应用于姿轨控，具有实用价值。因此，本文重点研究如何设计一种基于固体微型推力器阵列的一体化算法，并进行相关的仿真分析，验证算法的可行性及可靠性。

1 基于微型推力器阵列布局设计

微型推力器阵列不同于现有星上推力器，要根据其特点，设计合理的布局，使推力器阵列既能用于姿态控制，又要用于轨道控制，才能为算法设计奠定基础。

1.1 基于推力器阵列的控制特点

固体微推力器阵列中每个推力器只能使用一次，单个推力器冲量一定。当推力器位置固定后，其冲量矩也是一定的。通过不同的推力器组合，或者选择不同力臂的推力器来实现轨道和姿态的精控粗控，形成多种控制档次。

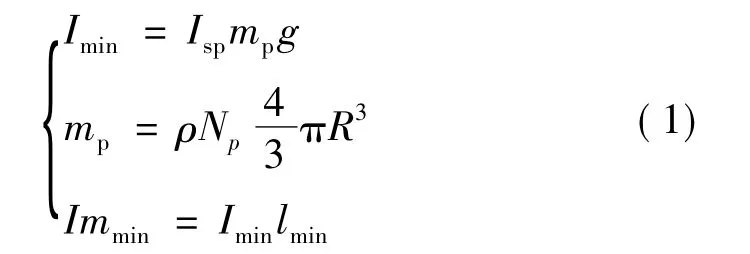
式中 Imin为最小冲量;Immin为最小冲量矩;Isp为推进剂的比冲;mp为推进剂的质量;Np为颗粒数目;R为颗粒半径;ρ为推进剂密度;lmin为推力器之间最小间距。

由式(1)可知，每个推力器可通过调整冲量关系式中的参数来改变冲量大小，现阶段研究的推力器总冲最小可达几十毫牛秒，为实现高精度控制提供一定基础;由于单个推力器体积小，集成度大，多达几百个推力器集成于一个阵列，因此可具有较高机动能力。

基于微型推力器阵列的控制误差由推力器的最小冲量和阵列能提供的最小冲量矩决定［7－8］。

1.2 推力器布局及阵列构型

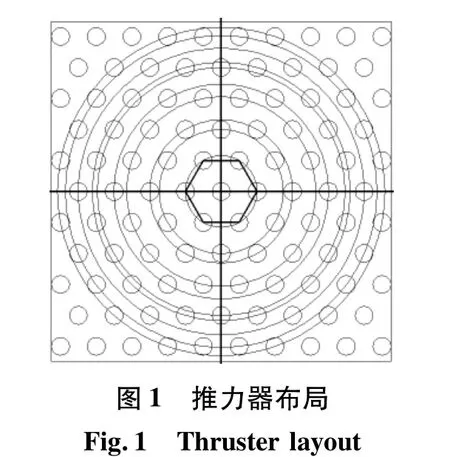
现有的推力器布局结构多数设计以正方形为基元［9－11］，本文设计了一种推力器布局方法，如图 1所示。该推力器阵列的基本生成元为正六边形，以正六边形的边长为推力器相隔间距，按式(2)向外扩展衍生出其他推力器位置，衍生的推力器个数由所需阵列规模大小决定。每一个推力器都将分布在以基本生成元正六边形的中心为圆心的某个圆周上，各个圆周上均分布着6个或12个推力器。

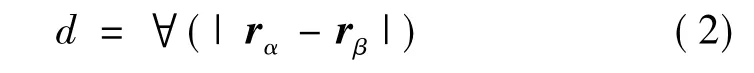
式中 rα、rβ为相邻2个推力器的矢量。

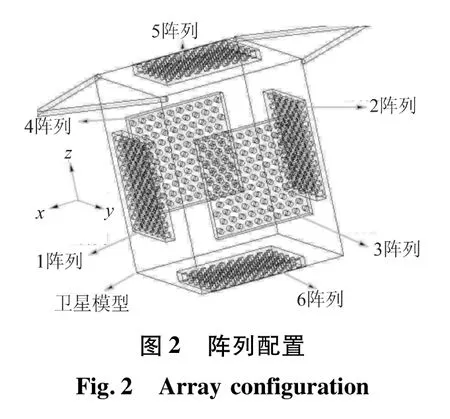
阵列的配置与任务的维数有关，如果进行六维控制，考虑三轴轨道控制和三轴姿态控制，本文选择正六面体的配置方式，如图2所示。在6个表面上布置6个推力器阵列，每个推力器阵列的中心方向通过卫星质心。

2 基于微型推力器阵列的算法

轨控和姿控往往是耦合进行的，因此需研究基于微型推力器阵列的一体化控制，即使用一套控制阵列，能同时对轨道和姿态进行控制。

2.1 问题描述

根据期望冲量和冲量矩，利用微推力器阵列来提供。

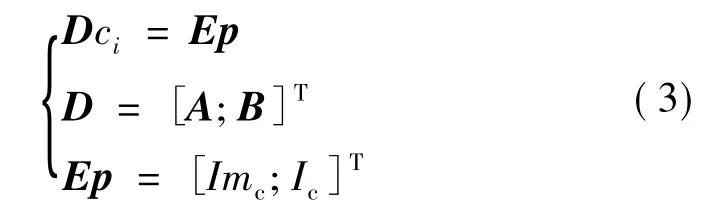
式中 A、B为根据推力器阵列求出的相应的冲量、冲量矩矩阵;Ep为所需的冲量和冲量矩;Imc为姿态控制所需冲量矩;Ic为轨道控制所需冲量;ci为决策变量，值为0或1。

推力器分配算法需要解决的问题就是在进行姿轨控时，根据所需的冲量或冲量矩，由算法求解出所需推力器组合，由微推力器阵列进行组合来产生。

2.2 星上推力器分配算法要求

(1)推力器控制分配的基本要求是求解出的推力器组合满足任务所需的冲量和冲量矩。

(2)能实现星上实时控制，要求卫星推力器的分配算法求解时间要求控制在毫秒级，否则卫星将很难进行控制。

(3)当轨控发动机失效，姿控发动机可用来进行轨控，虽然降低了使用寿命，但卫星仍可控。

2.3 算法选择

现阶段求解推力器分配问题，常用算法包括解耦法、伪逆法、线性规划法、最优查表法等，而本问题应用伪逆法及线性规划算法求解，变量数目多达百万级，迭代计算量巨大，无法求解［12－13］。最优查表法虽然可利用离线计算提前储存组合表，但需利用线性规划进行离线计算，因此仍无法计算［14］。

固体推力器只有点与不点两种状态，属于0～1规划问题。解决0～1规划问题常用的方法包括分支定界法、隐枚举法以及启发式算法、人工智能算法，这些算法能很好地充分利用推力器，但分支定界法、隐枚举法存在枚举，因此无法求解，而智能算法虽然能求解，但收敛速度慢，计算时间仍不能为实时控制所接受，且求解存在误差，这是对于精密控制所不能允许的。因此，这些算法同样无法进行实时控制［15］。

根据星上推力器分配算法要求，为了使推力器阵列具有实用性，放弃耦合算法，采用解耦方法，按指令分量方向将推力器进行分组，通过对消的方法使得每个组合仅在一个控制量方向上产生作用，虽然浪费一些推力器，但能满足控制要求，实现实时姿轨控，具有应用价值，将所提出的算法命名为“阵列规划算法”。

3 阵列规划算法

本文提出的阵列规划算法，能解决基于微型推力器阵列的推力器分配问题，以满足实时控制的要求。为便于研究，以10×11的推力器阵列进行说明，首先进行推力器及阵列的解耦分配。

3.1 推力器解耦控制分配

如图2所示，以3阵列和4阵列对Y方向推力的控制及对偏航轴的控制为研究对象。

3.1.1 姿轨控推力器分配

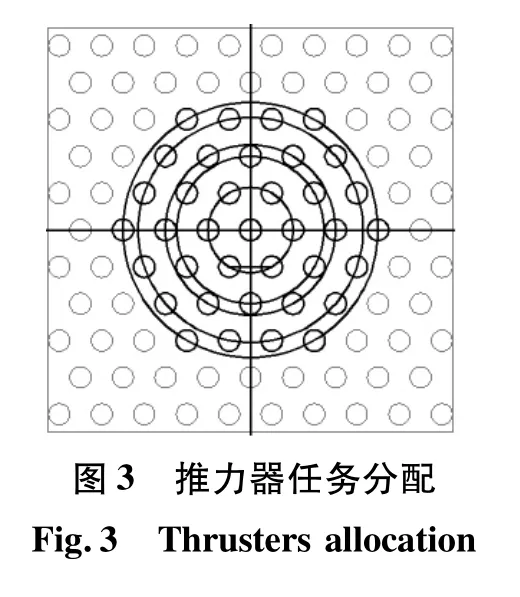
姿态控制所需力矩较小，而对轨道控制所需推力较大，阵列需要为姿态控制和轨道控制分配各自的推力器。如图3所示，设黑色圆周上的推力器用于轨道控制，而其他推力器用于姿态控制，根据不同任务可设计轨道控制、姿态控制的所需推力器的性能及分配各自所需推力器数量。

3.1.2 各个控制向量的阵列分配

阵列的配置方式，采用正六面体形式，如图2所示，假设进行六维控制任务，各个控制向量的阵列分配如表1所示。

3.2 姿轨控推力器分配建模

姿态、轨道单独控制，姿态控制通过前后2个阵列，以力偶的形式来提供冲量矩;轨道控制需要推力器组合合力通过卫星质心方向。用过的推力器设置其成本为一个很高的权值。

表1 控制向量阵列分配Table 1 Array allocation according to control vector

本算法优化目标是提高阵列使用寿命，即每次控制使用推力个数最少，且保留尽可能多的组合方式，以使推力器阵列具有较长的使用寿命。根据阵列特点，提出推力器成本的概念:每个推力器与其他推力器有多种组合，使用组合种类越少的推力器成本越高，组合种类多的成本低。优先使用成本低的推力器组合，保证推力器的组合种类的多样性。

3.2.1 轨道控制推力器分配建模

对于同一轨道控制任务所需的冲量，使用的推力器个数固定。因此，在保证合力通过卫星质心方向基础上，目标函数用于优化推力器组合，保留更多组合方式，提高阵列的使用寿命。

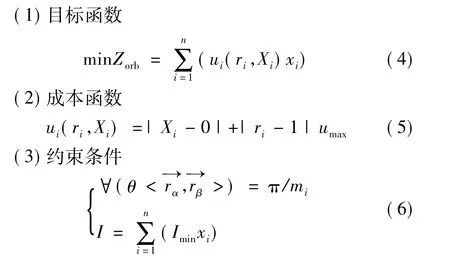
式中 ri表示每组的序列号，ri=1，2，3，…，n;mi表示推力器数量;ci表示决策变量0或1;Xi表示距离中心轴Y轴的距离;umax为一常数，umax=100;I为所需冲量;Imin为单个推力器冲量。

目标函数的目的为保证总成本最小;成本函数表示即使用距离阵列中心距离较小，且占用组数越少的推力器组合，则成本较小。约束条件用于保证满足控制任务所需的冲量。

3.2.2 姿态控制推力器分配建模

对于姿态控制所需的推力器数量是不确定的。因此，优化目标用于保证使用最少的推力器数量以及保留更多的推力器组合方式。

(1)目标函数

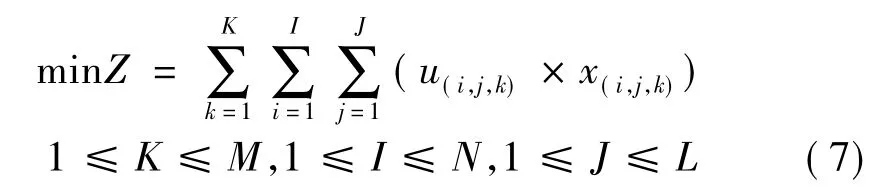
式中 k为所选推力器的行号;i为所选推力器阵列的列号;j为相对阵列的列号;M为相对阵列的行数，N为相对阵列的列数，L为阵列的行数，如100×110阵列，则N=M=100，L=110，若10×11阵列，则 N=M=10，L=11。

(2)成本函数

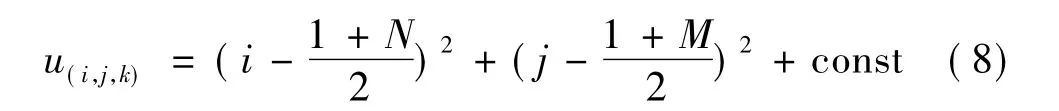
式中 const为一较大常数，该值根据阵列规模设置，需大于阵列中最大成本值。

(3)约束条件

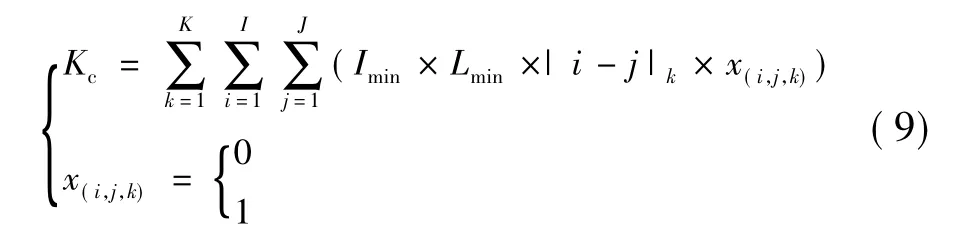
当选择了位于阵列第i列，其对应阵列第j列，第k行的推力器时，x(i，j，k)=1;否则 x(i，j，k)=0。

该模型可约束推力器单元如何进行组合提供所需的冲量矩，以达到利用率的最大化以及使用成本最低的目的。在满足约束条件的前提下，选择推力器数量越少，且选择组合方式多的推力器组合，则成本越小，从而可保证留下的推力器能提供更多的产生力矩的推力器组合形式。

3.3 阵列规划算法提出

虽然进行了解耦，但该模型求解，仍然无法使用求解0～1规划的常规方法，考虑到规模较大，采用分步、分阶段的方法，可采用动态规划、贪心算法等求解。但阵列中的推力器是一次性的，而每个推力器又有多种组合选择，因此具有后效性，每一阶段求出所需推力器后，会对下一阶段的选择产生影响，因此不直接使用动态规划和贪心算法求解，为求解该问题本文提出了一种“阵列规划算法”。

阵列规划算法主要思想:采用动态规划和贪心策略的思想［15－17］，分阶段计算，根据阵列的使用情况求出每行、每组的最大冲量矩和冲量，将所需值减去求解出的最大值，依次循环，直到全部实现，每一阶段的结果进行总结，即为所求解，每一个阶段受成本函数约束，选择成本最小的推力器组合。这样能够保证阶段数最少，状态变量数目最少，并且满足目标函数要求。该算法可大大降低计算复杂程度，能够满足实时控制需要。

3.4 建立求解模型

(1)状态转移方程

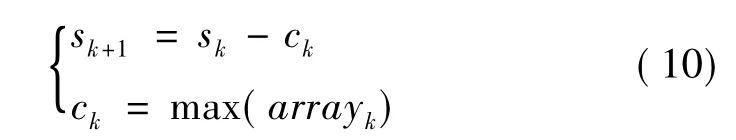
式中 ck为第k阶段的决策变量，为某一组或一行的最大值冲量或冲量矩;sk为第k阶段状态变量。

(2)阶段指标

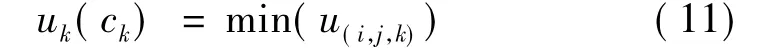
式中 uk(ck)表示选择成本最小的组合。

(3)最优指标函数模型

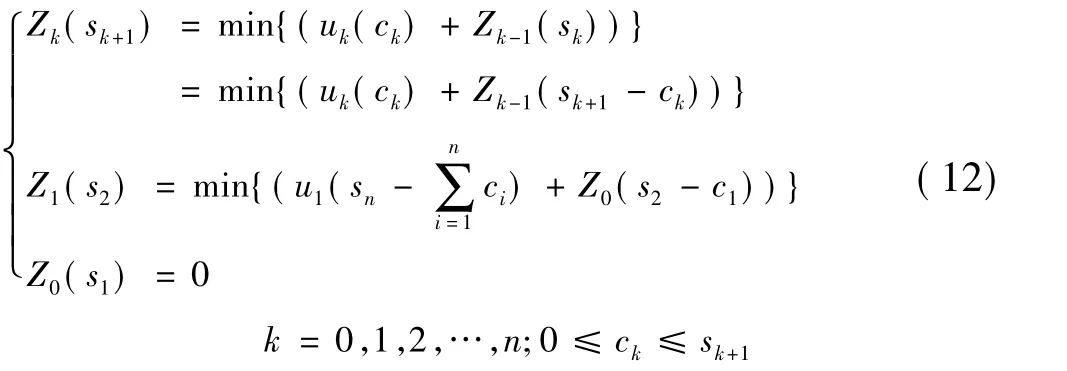
在求得各阶段最小成本后，求出对应的坐标(ik，jk，kk)。因此经过求解，可得出最优策略，已使用过的推力器组合成本设为最高值，最优策略为

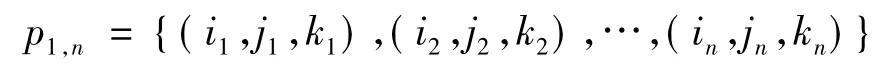
(4)使用矩阵建立

姿态控制使用矩阵为m×n的0～1矩阵，初始值为0，当推力器使用后改写为1。同理，轨道控制推力器6个分为一组，n′为组数，因此形成n′×6的0～1矩阵。

(5)成本矩阵建立

轨道控制所需冲量由2、3、4、6单位的冲量组合产生，因此需产生4种成本表。姿态控制的成本表由阵列的列数决定，对于m×n阵列，每行可产生1～(n－1)个单位的冲量矩，因此需设置n－1种成本表。

成本矩阵根据成本函数设置，对已使用的设为一个很高的权值，该值需大于阵列中成本的最大值。

3.5 姿轨控算法信息共享

姿控推力器和轨控推力器布局的方法一致，因此必然存在一定联系。为了更好地交互信息，保证点火可靠性，需进行姿轨控推力器之间的关系转换。

3.5.1 姿轨控推力器互为备份

由图3可知，根据不同的任务需要，对姿控和轨控的推力器进行分配。该分配的实现是通过对使用矩阵的设置来实现，在姿控算法中的使用矩阵，用于姿控的推力器设置为0，而用于轨控的推力器设置为1。同样，在轨控算法中，用于轨控推力器设置为0，而用于姿控的推力器设置为1。

通常为了增加控制可靠性，姿态控制推力器、轨道控制推力器需进行相互备份。备份的实现可通过对姿控和轨控的推力器使用矩阵进行0、1设定，来改变推力器的用途。例如，将姿态控制推力器作为轨控使用，可将姿态算法中的需要作为轨控的推力器设置为1，而将轨控算法中相应的推力器设置为0，以此来变换推力器的用途，从而可现实互为备份。

3.5.2 建立姿轨控推力器坐标转换

姿态控制和轨道控制公用一个阵列，各自算法之间需要进行信息交换，防止重复使用已用过的推力器，有利于进行点火控制输出。

将推力器在阵列中实际位置命名为物理坐标，在阵列中的以行列形式表示推力器的位置命名为阵列坐标。

推力器坐标最终传输给点火系统，因此需转化成第m行第n个推力器，即(m，n)，姿态控制寻址方式按照行寻址，寻址中用到的坐标与使用矩阵坐标一致，因此可直接将所需推力器坐标传输到点火系统。而轨道控制，因为以6个推力器为一组进行分组，因此需将其转换成(m，n)的形式，先将轨控推力器在使用矩阵中的坐标位置转换成物理坐标x，y。

设推力器坐标为x，y，则可获得坐标转换关系:

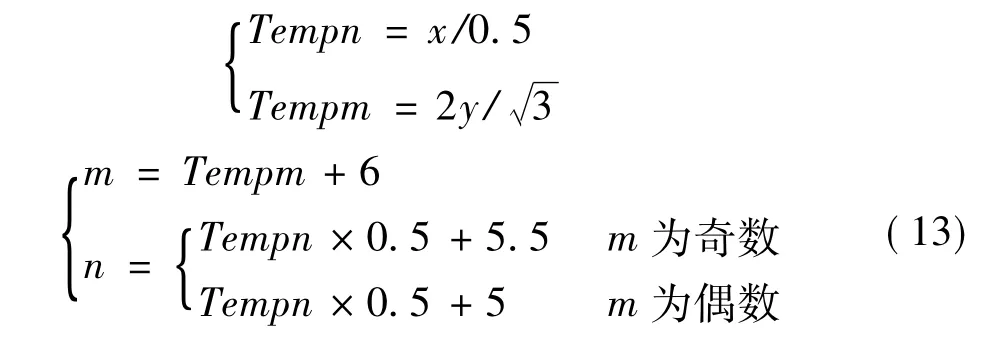
式中 Tempn、Tempm都为临时储存器。

尤其在进行姿轨控推力器更换用途时，可根据该关系进行推力器的标记。

3.6 算法分析

该求解算法能有效地求解基于微型推力器阵列的分配问题，求解效率高，每个阶段使用成本最小的组合，保证了使用推力器个数最少，并保证了推力器组合的多样性，在一定意义上提高了阵列的使用寿命。

3.6.1 算法运算规模分析

采用阵列规划算法，避免了枚举，姿态控制降低为每阶段寻址规模最大为m(n－1)，时间复杂程度上界为O(m(n－1))，下界为O(n);轨道控制每次寻址规模最大为6n′(n′为分组数)。图4给出了10×11阵列分别全部用于轨道控制和姿态控制时计算规模曲线图。如果使用空间换取时间，将其各成本制作为表格，每次进行查找表计算，则计算时间将会更短，但需要占用更多储存空间，可进行时间和空间的权衡，选择合适的成本表数量。

3.6.2 推力器个数使用最少证明

在轨道控制所需冲量一定情况下，使用推力器个数是固定的。因此，对轨道控制推力器的使用情况不加证明。

证明阵列规划算法－姿态控制算法保证使用推力器个数使用最少，采用反证法证明。

证明:因为每个阶段都需2个推力器组合，设某次总共需要n个阶段，共需推力器个数为2n，如果该组合不为最佳，设需要的推力器个数为2(n－1)个，则某一阶段存在更大的冲量或冲量矩，与每次选择最大的冲量或冲量矩矛盾。因此，该策略下能保证推力器个数最少。

4 算例仿真验证

基于微型推力器阵列的皮纳卫星能进行高精度和快速机动的姿轨控，对于空间交会对接、空间攻防、编队飞行等，都有着重要的应用前景。

该算法采用了解耦的方式，因此仿真只验证一对阵列的寻址控制效果。

阵列的规模可根据任务需要进行设置，不就具体任务进行分析，只需进行算法仿真验证，看是否符合设计要求。

由微型推力器阵列特点可知，基于推力器阵列的控制精度由最小冲量和冲量矩决定，不需将误差考虑到数学模型中，每次控制根据要求进行圆整为最小冲量矩和冲量的整数倍，再进行算法求解。

对于某次任务，根据所需冲量和冲量矩，经过仿真所需推力器组合如表2所示。点火后的阵列使用情况如图5所示。

以第1次调整为例进行说明，滚转所需冲量矩为10Immin，Y方向所需冲量为6Imin，因为阵列没有使用，该阵列能提供的最大冲量矩为9Immin，所以示分阶段产生9Immin和1Immin。由3.2.2节内容可知，选择3阵列中坐标为(1，1)和4阵列中坐标为(1，10)产生9Immin，由3阵列中坐标为(1，5)和4阵列中坐标为(1，6)产生1Immin的成本最小，能保证推力器使用个数最少。

Y方向的冲量由3阵列中的坐标为(5，5)、(5，6)、(6，4)、(6，6)、(7，5)、(7，6)，即为距离中心最近的第一组圆周上的推力器。由3.2.1节内容可知，该组合距离阵列中心最小，占用组数最少，成本最小。同理，可说明其他调整次数中成本亦为最小，推力器个数最少，保留了较多的推力器组合方式。

现假设轨控推力器失效，或者轨控推力器已用完，仍需进行轨控，则需使用姿态控制来代替。由于姿控发动机仍按1.2节中的方法布局，因此能保证合力方向通过卫星质心。设某任务需要10Imin，通过姿控推力器来进行控制，如图6所示。使用了10个姿控推力器来进行轨控，其坐标为(2，5)、(2，6)、(3，3)、(4，2)、(4，8)、(8，2)、(8，8)、(9，8)、(10，4)、(10，5)。由图6可知，所有推力器合力通过阵列中心方向，即卫星质心方向，该组合成本为最小。

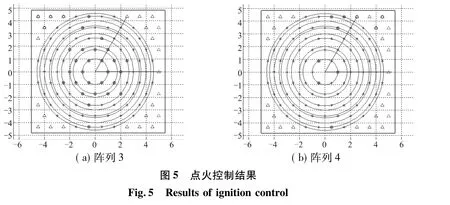
表2 控制仿真Table 2 Control simulation

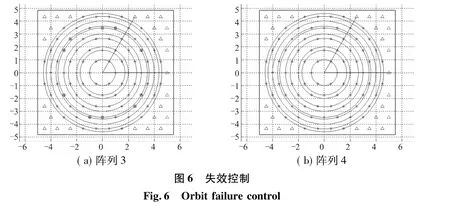
经过仿真验证了算法的可行性，说明本文设计的推力器布局方法具有较高的纠错能力。

5 结论

(1)所设计的推力器布局方式能满足姿轨控需要，对于姿轨控可分配各自所需的推力器，能实现一体化控制，且该结构利于姿轨控推力器互为备份;

(2)建立的推力器分配数学模型能保证使用最少的推力器以及保证了推力器组合的多样性，提高推力器阵列的使用寿命;

(3)基于微型推力器阵列的姿轨控具有较高的失效纠错能力，能实现信息共享，可有效地进行互为备份;

(4)所设计的求解算法能满足姿轨控实时控制需要，求解规模小，搜索效率较高，计算准确，满足成本目标函数要求。

［1］Larangot B，Conédéra V，Dubreuil P，et al.Solid propellant microthruster:an alternative propulsion device for nanosatellite［J］.Aerospace Energetic Equipment，2002:12－14.

［2］Chaalane A，Larangôt B，Rossi C.Main directions of solid propellant micro－propulsion activity at LAAS［C］//CANEUS 2004 － Conference on Micro－Nano－Technologies.Monterey，USA，November 1－5，2004.

［3］Jongkwang L ，Dae Hoon L and Sejin K.Design and performance evaluation of components of micro solid propellant thruster［C］//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Fort Lauderdale，USA，July 11－14，2004.

［4］Amanda A Green.Demonstration and quantitative characterization of a MEMS fabricated propulsion system for the next generation of microspacecraft［C］//39th AIAA Aerospace Sciences Meeting ＆ Exhibit.Los Angeles，USA，January 8－11，2001.

［5］Pablo A Servidia，Ricardo Sánchez Peña.Spacecraft thruster control allocation problems［C］//IEEE Transactions on Automatic Control，2005，50(2):245－249.

［6］Andersen F，Shu－Fan Wu.Optimization of spacecraft thruster management function［C］//AIAA Guidance，Navigation，and Control Conference，2005，28(6):1283－1290.

［7］Mueller J.Thruster options for microspacecraft:a review and evaluation of existing hardware and emerging technologies［C］//AIAA/ASME/SAE/ASEE Joint Propulsion Conf.and Exhibit，AIAA 97－3058.

［8］Kaili Zhang，Chou S K，Simon S Ang.MEMS－based solid propellant microthruster design，simulation，fabrication，and testing［J］.Journal of Microelectro－Mechanical Systems，2004，13(2):165－175.

［9］David H Lewis Jr，et al.Digital micropropulsion［J］.Sensors and Actuators:Physical，2000，80(2):143－156.

［10］Rossi C，Conto T Do，Est`eve D，et al.Design，fabrication and modelling of MEMS－based microthrusters for space application［J］.Institute of Physics Publishing，2001:1156－1162.

［11］唐生勇，张世杰，等.交会对接航天器推力分配算法研究［J］.宇航学报，2008，29(4):1120－1125.

［12］Doman D B，et al.Control allocation of reaction control jets and aerodynamic surfaces for entry vehicles［C］//AIAA Guidance，Navi－gation，and Control Conference and Exhibit，AIAA 2007－6778.

［13］Bard S Crawford.Configuration design and efficient operation of redundant multi－jet systems［C］//Proc.of AIAA Guidance Control and Flight Mechanics Conference，1969:69－845.

［14］王敏，解永春.考虑推力器上届及故障情况的航天器实时指令分配最优查询表［J］.宇航学报，2010，31(6):1540－1546.

［15］Frederick S Hillier，Gerald J Lieberman.运筹学导论［M］.北京:清华大学出版社，2009:424－491.

［16］王晓东.计算机算法设计与分析［M］.北京:电子工业出版社，2009:9－121.

［17］陈玮，解永春.基于多目标规划的交会对接推力器指令分配方法［J］.航天控制，2007，25(3).