关于约束最优化问题K-T条件的一点注记

展丙军

(大庆师范学院 数学科学学院，黑龙江 大庆 163712)

1 问题的提出

约束最优化问题的局部最优解是满足K-T条件。要想很好地回答这个问题并非易事，在绝大多数的教材、资料的论述中，都要做很多前期工作，给出若干个引理或定理，然后才能推证结论，整个过程篇幅过大，不仅繁琐，而且对“高难度”知识过分地依赖。因此，有些教材、资料只给出结论，而略去了证明，这些都给读者带来很大的不便。目标函数、约束函数的条件的不同，可以得到不同形式的K-T条件，证明方法也就不尽相同，找到论证约束最优化问题的最优性条件(即K-T条件)的新方法有着重要的意义。在运筹学的教学中，发现K-T条件与用拉格朗日乘数法所确定的极值条件很相似，受此启发得到解决上述问题的便于理解、掌握的新方法。

2 约束最优化条件(K-T条件)的证明

其中，x=(x1，…，xn)T∈Rn，f：Rn→R1

gi：Rn，→R1，i=1，…，P，hj：Rn→R1，j=1，…，q

下面给出上述问题的最优解的必要条件，即约束最优化条件：K-T条件。

定理1 设f：Rn→R1和gi：Rn→R1，i∈I(x*)，在点x*的某邻域内连续可微，gi∈II(x*)，在点x*处连续，hj：Rn→R1，j∈J，在点x*的某邻域内连续可微，并且各gi(x*)，i∈I(x*)，hj(x*)，j∈J(x*)，线性无关。若x*是(MP)的局部最优解，则存在两组实数和使得

(1)

将(1)式称为(MP)的Kuhn-Tucker条件，简称为K-T条件。

证明：

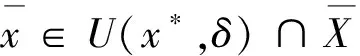
Φ的稳定点(也称驻点)xk，k=1，2，…，它们都是可能的极值点，特别地，x*也满足个列条件：

(2)

hj(x*)=0

上式恰为K-T条件(1)的第一个式子。

综上所述，命题成立。

下面补充说明定理的条件的确定。一方面，对f，gi，hj的可微性、连续性的要求是为了保证能用微积分的方法进行研究。另一方面，如果，gi(x*)，i∈I(x*)，hj(x*)，j∈J，线性相关，必然存在一组非零的常数和使hj(x*)=0，又因为hj(x*)=0，所以f(x*)=0，这样x*相当于无约束问题z=f(x)的极值点，原有的约束失去了作用，这不是我们要讨论的(MP)问题。所以，要求gi(x*)，i∈I(x*)，hj(x*)，j∈J线性无关。

将定理1中的条件稍加改变，有如下的定理：

定理2 设f∶Rn→R1，gi∶Rn→R1(i∈I)和hj∶Rn→R1(j∈J) 都在点x*的某邻域内连续可微，并且各gi(x*)，i∈I，hj(x*)，j∈J，线性无关。若x*是(MP)的局部最优解，则存在两组实数和使得

(2)

值得说明的是，定理1的条件中，设f∶Rn→R1和gi∶Rn→R1，i∈I(x*)，在点x*的某邻域内连续可微，hj∶Rn→R1，(j∈J) ，在点x*的某邻域内连续可微，改为设f∶Rn→R1和gi∶Rn→R1，i∈I(x*)，在点x*处可微，hj∶Rn→R1，(j∈J) ，在点x*处连续可微，结论仍然成立，但改后定理的证明方法不能用上述的方法，因为上述证明方法中，用到了拉格朗日乘数法，拉格朗日乘数法要求给定的函数在点x*的某邻域内连续可微；另一方面，在实际计算中，即在用K-T条件求K-T点时，要做求f(x)，gi(x)，hj(x)的运算，也是要求在点x*的某邻域内连续可微的，几乎不会只在一点x*处连续可微的条件下讨论问题，况且，定理中点x*是假设的点，不知道在哪。所以，在实际应用中，按本文定理1、定理2给出f，gi，hj的条件是更有实际意义。

3 结语

本文给出了f，gi，hj满足两种不同情况下约束最优化问题的最优性条件(即K-T条件)，并用新的方法论证了这两种情况下的K-T条件，这种方法便于理解和掌握。定理中，f，gi，hj的条件要求强了些，正如前述，它的应用价值不但不受影响，反而提高了。将此成果应用于教学，起到了很好的效果，有利于激发学生的学习积极性和探索精神。

[参考文献]

[1] 刁在筠，刘桂真，宿洁，等.运筹学[M].3版.北京:高等教育出版社， 2007:131-136.

[2] 解可新，韩立兴，林友联. 最优化方法[M].天津：天津大学出版社，2002：139-152.

[3] 刘玉琏，傅沛仁，林玎，等.数学分析讲义：下册[M].4版.北京:高等教育出版社，2003:231-232.

[4] 吴祈宗. 运筹学[M].北京：机械工业出版社， 2002.

[5] 宁宣熙. 运筹学实用教程[M].北京：科学出版社，2002.