基于多尺度小波谱的桥梁结构非一致地震响应分析研究

杜 鹏，贾俊梅

（1.天津市市政工程设计研究院，天津市 300051；2.中交第一航务工程勘察设计院有限公司，天津市 300222）

0 前言

目前，随着我国经济的发展，许多大跨度桥梁相继建成。为了保证大跨度桥梁的抗震安全，需要对其进行专门的抗震分析。在以往的桥梁抗震设计中，人们趋向于只考虑单点平动输入下的结构反应，然而随着近年来地震观测资料的不断丰富，人们发现地震波在沿大跨度结构传播过程中会有显著的变化[1]，从而导致结构不同支点的运动明显不同，因此采用多点非一致激励对大跨度桥梁进行地震反应分析显得十分的重要。

引起地震动时空变化的因素归结起来有以下几个方面[2]：一是“行波效应”；二是“部分相干性的影响”；三是“局部场地效应的影响”。可以看出，一致激励实际上相当于多点非一致激励作了波速无穷大、各个支点运动完全相干、场地均匀等假定后的简化模型。

在求解大跨度结构地震响应方面，DerKiureghian和Neuenhofer[2]、Loh和Ku[3]提出了基于反应谱的方法去考虑地震动的空间效应。这些研究都是基于地震动为平稳随机过程的前提下提出的，而且其计算效率及精度都存在不小的问题[4]。但是，众所周知，地震动是一个强非平稳过程，对于地震动非平稳模型的模拟，一些学者也提出了一些拟合模型，如：Kameda[5]，Li和 Kareem[6-8]，Conte Peng[9]提出 的 一 维 非 平 稳 拟 合 模 型 ，Li 和 Kareem[6，8]，Deodatis[10]提出的多维非平稳拟合模型，以上这些学者在提出地震动非平稳拟合的时候都没有提出好的估计地震波演变功率谱密度的方法，因此这些方法应用起来并不方便。

本文在前人工作的基础上，基于小波理论对非平稳地震动过程进行了合理的拟合，该荷载模型不但可以模拟非平稳荷载幅值及频率同时为非平稳过程的特性，而且该模型还考虑了多点激励下荷载行波效应及场地土部分相干性的影响;其次，本文基于小波理论多点激励下结构的动力方程在小波域内对结构的响应进行求解，得到了结构响应的瞬时功率谱密度函数和响应瞬时均方值的表达式，最后，本文利用一个三跨连续梁桥的算例，对所提的方法进行了验证。

1 非一致地震激励的多尺度小波谱模拟

考虑到大跨度结构多点激励问题，可以将任一个支点的非平稳地震动激励用x¨gr（t）来表示，其中r=1，2，…，n，表示支点的位置，而第 r个支点的地震动x¨gr（t）可以用Priestly提出的演变随机过程[11]的公式来表达：

式（1）中Ar（t，ω）为随时间和频率同时变化的确定性调制函数，而dGr（ω）表示对应支点处的正交增量过程，其中：

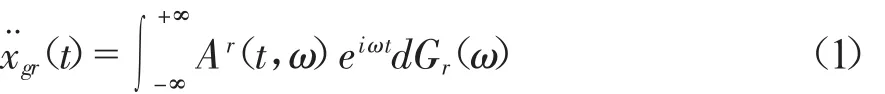
然后，对于x¨gr（t）在任意一个给定尺度aj上进行小波变换并将式（1）带入其中可以得到：

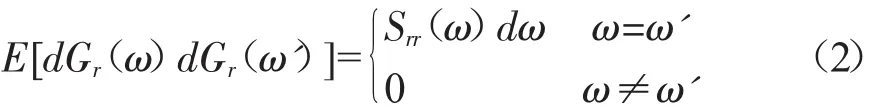
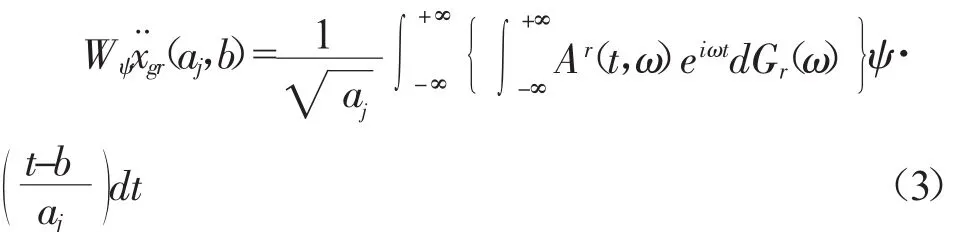
由于小波基函数的局部化特性，可以近似认为Ar（t，ω）在时刻b附近不随时间发生波动；并且，由于调幅函数是一个慢变函数，因此可以近似地认为，在尺度aj所对应的频带上调制函数Ar（b，ω）不随频率变化，从而式（3）可以表示为：

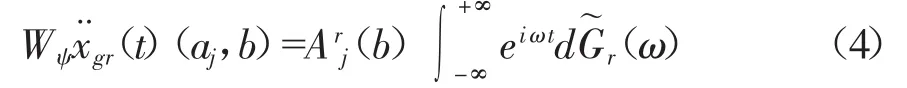
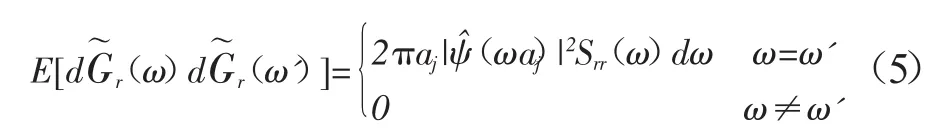
其中：

其中：Arj（b）为在aj尺度上的确定性均匀调制函数，在每一个尺度上Arj（b）为不同的均匀调制函数，由此可以看出，模拟的随机过程本质上是一个分段平稳过程，但此分段平稳过程可以根据所要模拟的非平稳过程的局部特性来划分频带的宽度，从而根据不同的频带宽度来选择均匀调制函数的形式。由式可以得到不同支点处地震波小波系数的互相关函数在尺度aj上的表达式：

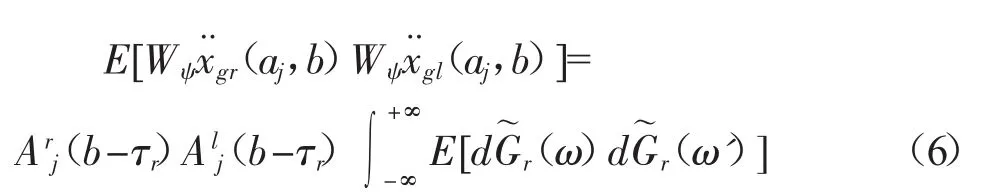
其中：

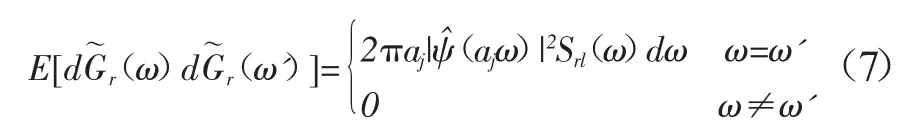
在式（6）中，τr分别代表频带j上的地震波从到达结构第一个支点到第r个支点传播的时间，τr=Lr/Vj其中Lr代表第一个支点和第r个支点之间的距离，Vj代表在尺度j上地震波传播的速度；同样τl与Ll也具有同样的意义。式（7）中的E[dG~r（ω）dG~l（ω'）]表示在支点r和l处正交过程的互功率谱密度，其可以表示由于行波效应引起的地震动空间相关性。其中，支点r和l之间地震动的互功率谱密度可以表示为：

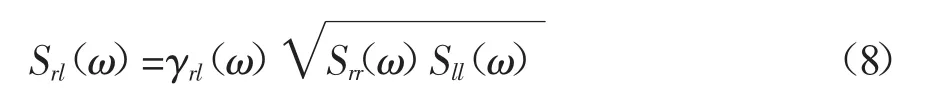
其中：γrl（ω）为不同支点处地震动的相干函数。

由此，式（6）为不同支点处地震动荷载小波系数的互相关函数的表达式，也可以说式（6）为地震动荷载的小波谱表达式，该式表征非一致随机激励荷载的统计特性。

2 大跨度结构体系非平稳随机响应分析的小波方法

对于有N个地面支座、n个自由度的离散线性结构，在多点激励下求解结构地震响应的基本运动方程可以写成如下形式[13]：

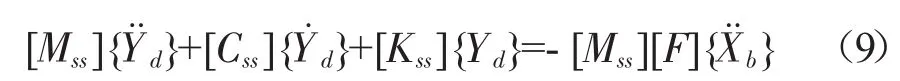
式（9）为多点激励下n个自由度结构体系地震响应的运动方程，而结构的地震响应可以表达为振型向量{φ（j）}（j=1,2，…，n）与广义坐标ηj（t）（j=1，2，…，n）乘积之和的形式，即：

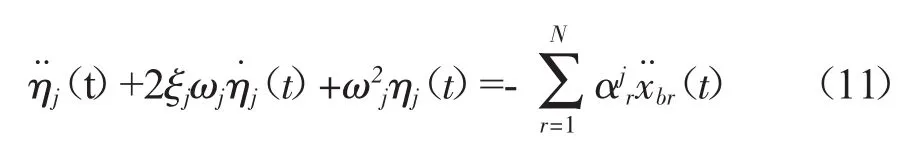
当结构的阻尼为比例阻尼时，式（9）可以解耦为n个单自由度结构的动力方程，其结构响应即为式（10）中的广义坐标，其中第j个振型所对应广义坐标的动力方程为：其中：ωj，ξj，αjr(={φ（j）}T[Mss]{F（r）}/{φ（j）}T[Mss]{φ（j）})分别表示第j阶模态的固有频率、阻尼比及振型参与系数。

对式（10）两边进行连续小波变换可以得到结构响应的小波系数，其中第i个自由度对应的小波系数为：其中：φi（j）为振型向量（φ（j））中第i个元素，对式（12）两边取平方期望可以得到：

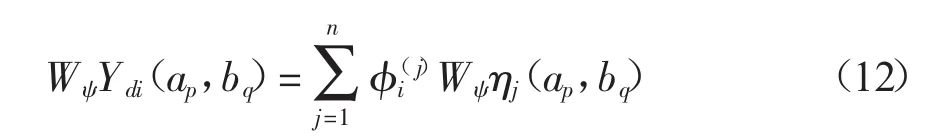
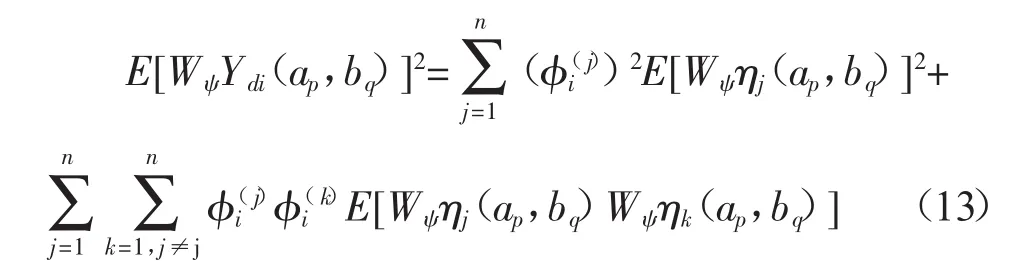
为了确定式中（13）每一阶振型所对应的广义坐标的自相关小波系数与互相关小波系数，将ηj（t），x¨br（t）按照Alkemede提出的离散化方案[14]进行离散化，该离散化的形式是令：aj=σj，bj=（j-1）Δb，由此可以得到：

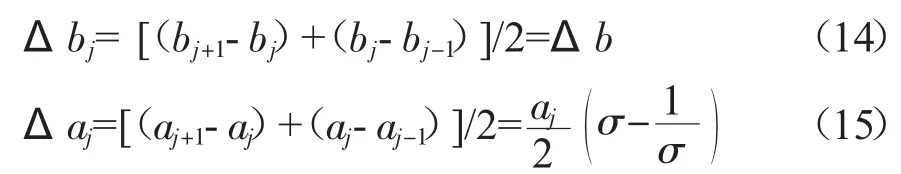
利用此离散化形式，ηj（t），x¨br（t）可以写为：

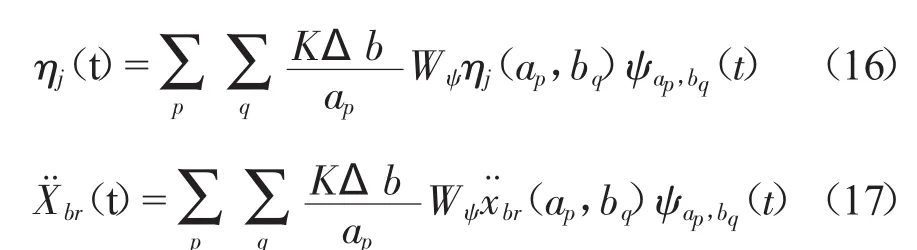
其中）。

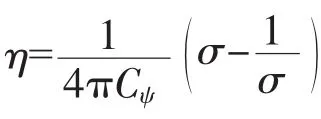
将其代入到式（11）中并对方程的左右两边进行Fourier变换可以得到：

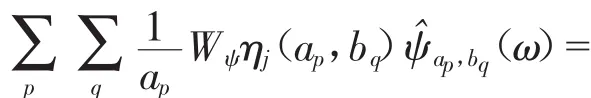
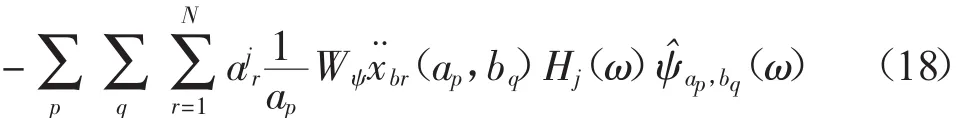
其中：

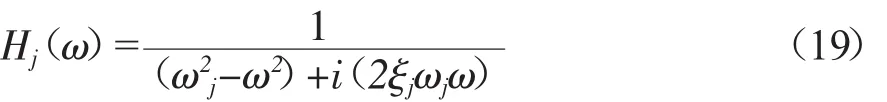
为了对式进行化简，小波基函数选取Basu与Gupta提出的正交小波基函数[12]，式（18）可以化简为：

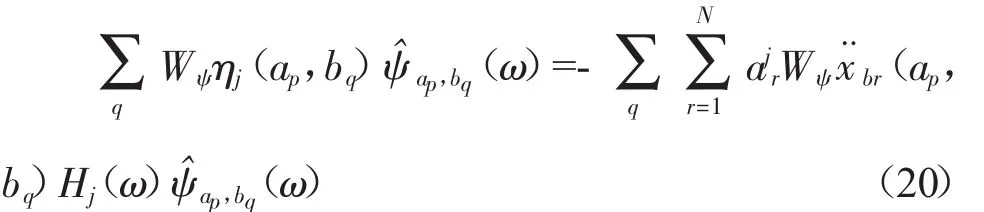
对于第k阶振型所对应的广义坐标ηk（t）同样也可以得到类似的形式：

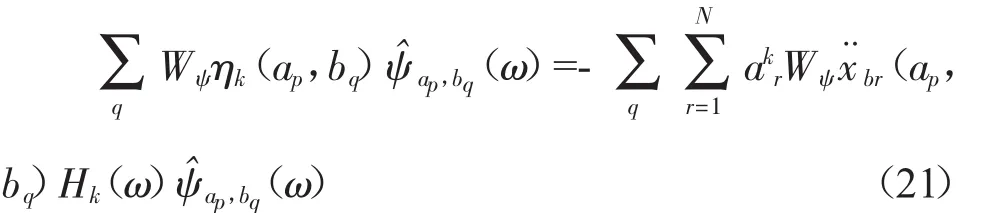
对式（21）两边取共轭并与式（20）两边相乘并取期望，然后在方程左右两边对自变量ω进行积分，根据小波基函数的正交性可以得到：

当j=k时

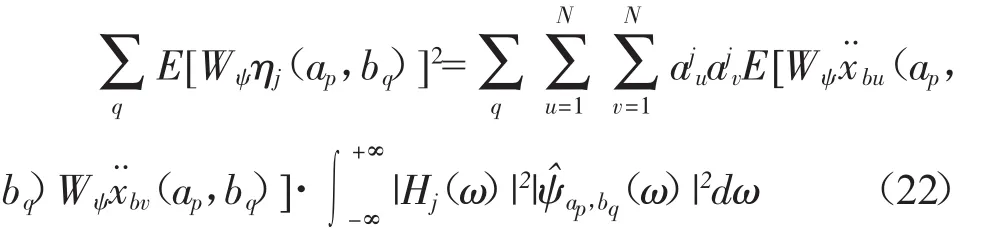
当 j≠k 时

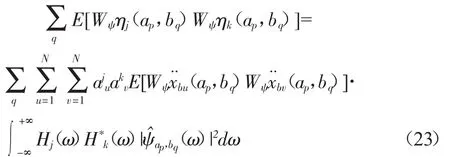
根据文献[12]所述，激励小波系数在不同时刻的互相关系数项之和趋近于零，所以被省略掉了。根据Paserval定理可以知道Ydi（t）在所有频带总能量的平均值可以表示为

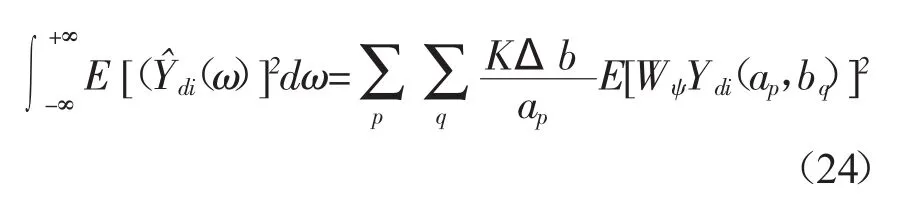
将式（13）、式（22）及式（23）代入到式（24）中来可以得到：

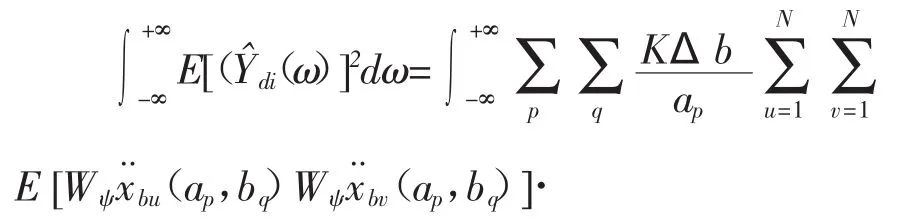
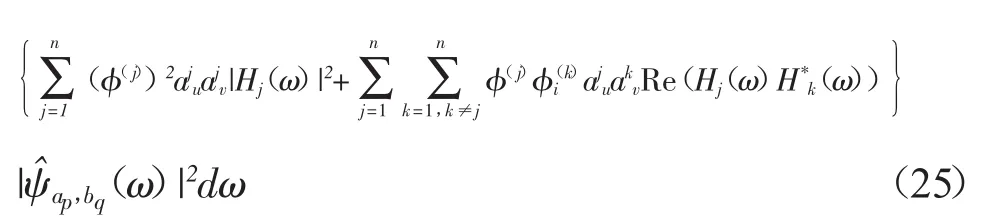
结构响应Ydt（t）在尺度ap所对应的频带内的瞬时均方能量为：

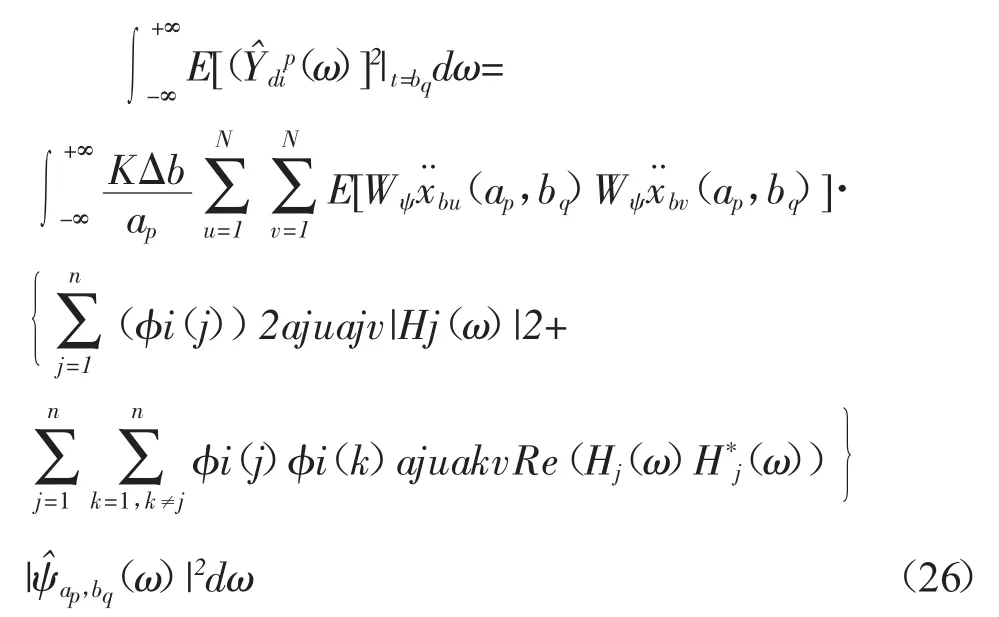
当σ≈1时，对于每一尺度ap小波基函数所对应的频带很窄，即式（26）的积分区间很小，因此可以近似地认为被积函数相等，由此可以得到结构响应的瞬时功率谱密度函数的表达式为：结构响应的瞬时均方值可以表达为：

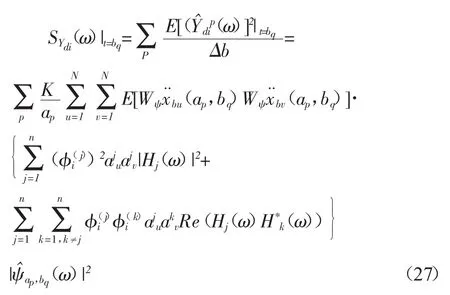
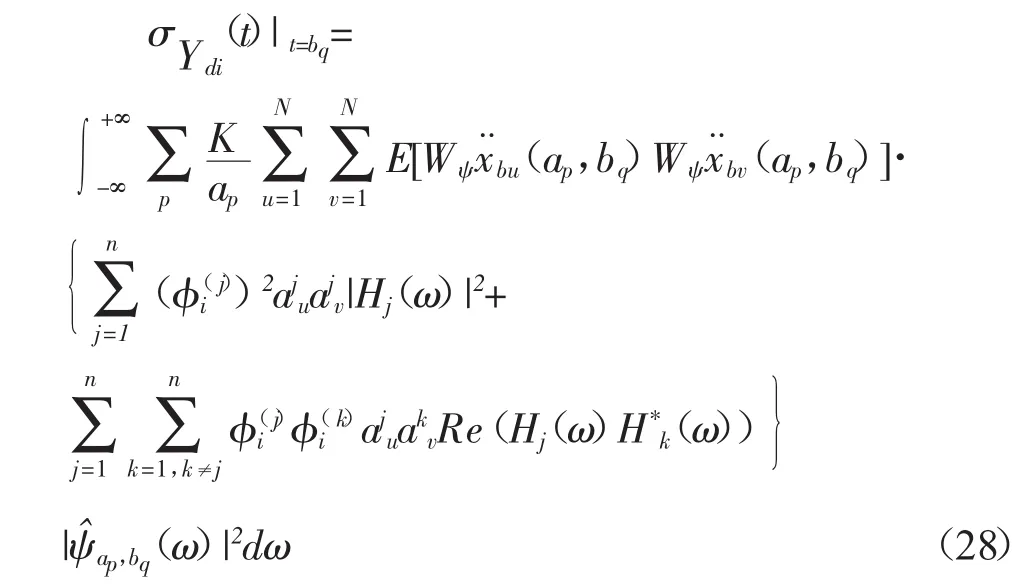
同理，也可以根据以上的推导过程得到结构拟静态位移响应的瞬时功率谱密度与瞬时均方值的表达式，其表达式如下所示：

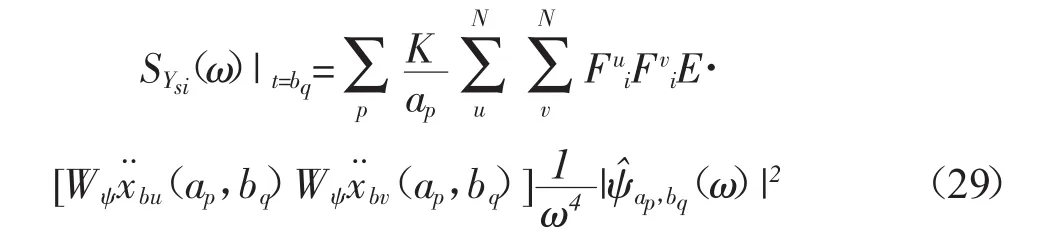
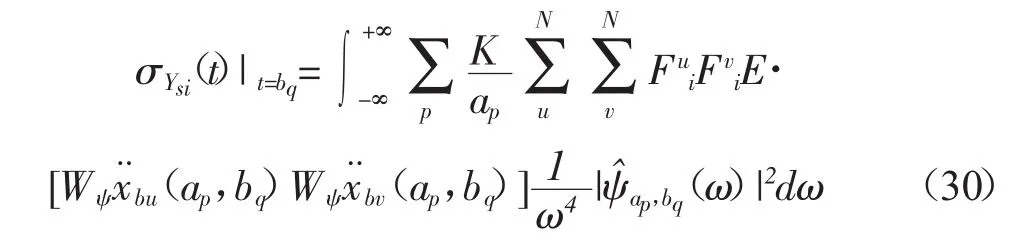
其中：Fui为支座第u个自由度方向的单位位移在结构第i个自由度上产生的力，其它符号的意义与式（27）、式（28）相同。

则结构相对地面的总位移响应的瞬时功率谱密度为：

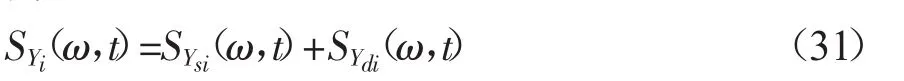
结构相对地面的总位移响应的均方值为：

3 三跨连续刚构桥数值算例

3.1 工程概况

本文采用的三跨连续刚构桥是武汉天兴洲公铁两用长江大桥公路引线工程南岸部分和平大道段的一座桥梁，其位于武昌区的和平大道处。本区段全长206 m，采用（58+90+58）m一联的三跨连续刚构桥，按汽车6车道设计，梁的全断面为单幅结构分离式直腹单箱单室箱形梁，按桥中心线对称布置，桥面采用结构找坡，全联平曲线3 500 m，其总体布置和箱梁截面尺寸如图 1～图 3所示。箱梁顶宽13.49 m，底宽7 m，中(边)跨梁高由跨中(端部)2.4 m变化到根部5.0 m，梁下缘变化按圆曲线设置。跨内两墩分别高33.044 m(1#墩)和31.77 m(2#墩)，均采用7 m×4 m矩形空心薄壁墩，壁纵向厚0.9 m，横向0.6 m。梁体采用挂篮对称悬臂现浇，边跨箱梁和桥墩连接处设GPZ3.5DX和GPZ3.5SX盆式橡胶支座，路面铺装采用100 mm厚改性沥青混凝土。其场地土类别为III类，抗震设防烈度VI度。

3.2 计算模型参数及其动力特性

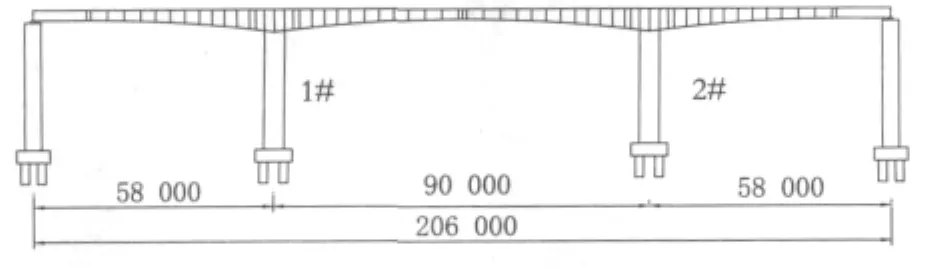
图1 连续刚构桥结构总体布置图（单位：mm）

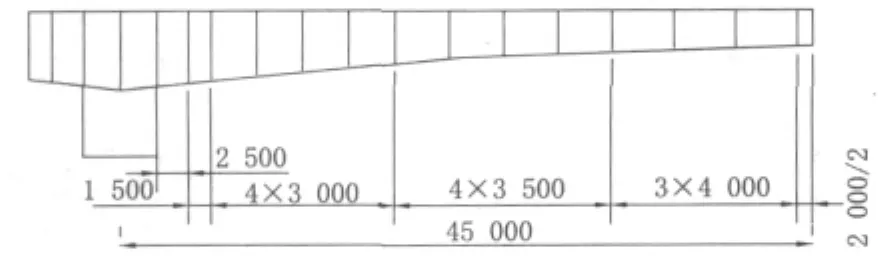
图2 连续刚构桥机构剖面布置图（单位：mm）

本文首先用通用有限元软件ANSYS对连续刚构桥进行平面杆系建模，然后将模型的质量，刚度矩阵导出，利用自编的MATLAB及FORTRAN程序进行桥梁的地震响应分析。全桥共离散成89个节点，其中主梁75个节点，桥墩14个节点，主梁及桥墩均采用平面梁单元BEAM3进行建模，为了计算简便将左右边墩简化成两个支座，支座仅约束主梁的竖向位移，主梁的混凝土强度等级为C50，桥墩为 C40，泊松比 0.1667，混凝土容重26 000 N/m3。

利用上述所建立的有限元模型，用子空间法计算了该桥的前8阶的频率，周期及其振动形式，如表1所示。

图3 箱梁及墩身截面尺寸（单位：mm）

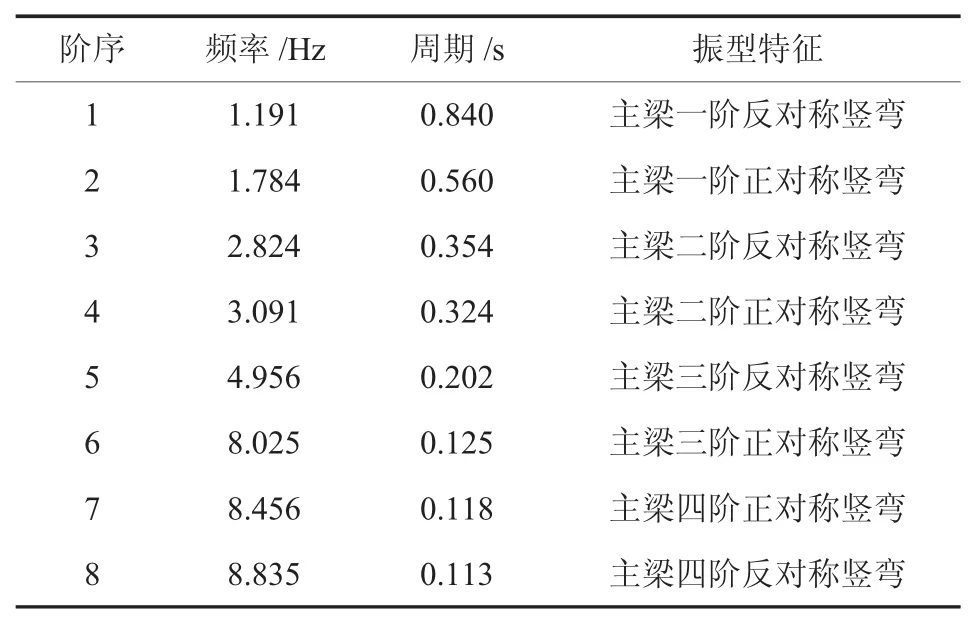
表 1计算模型前8阶自振频率及振型特性

3.3 三跨连续梁桥在实际地震动作用下响应分析

本小节选取的实际地震动记录为SMART1台网所记录的地震动E-45的45条地震波进行统计计算，调制函数Gamma模型[15]，其参数按照表2选取，地震动自功率谱密度模型选择胡聿贤模型[16]，其参数按照表 3进行选取地震波的波速为v=1 000 m/s，加载方向为顺桥向加载。

3.3.1一致激励情况

从图4及图 5可以看出，在一致地震激励作用下由实际地震动计算统计得到的结构响应的瞬时均方根值与由本文统计得到的荷载模型计算得到的结构响应的瞬时均方根值基本一致，但是计算速度比用时程分析方法的计算速度快很多。

3.3.2非一致激励情况

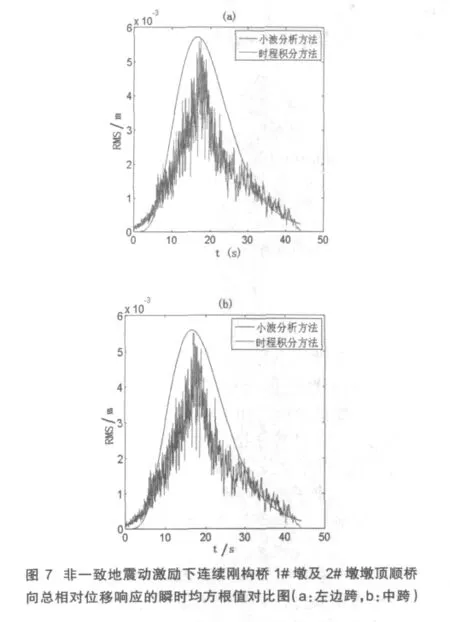
从图6及图7可以看出，在非一致地震激励作用下由实际地震动计算统计得到的结构响应的瞬时均方根值与由本文统计得到的荷载模型计算得到的结构响应的瞬时均方根值基本一致，但是计算速度比用时程分析方法的计算速度快很多。

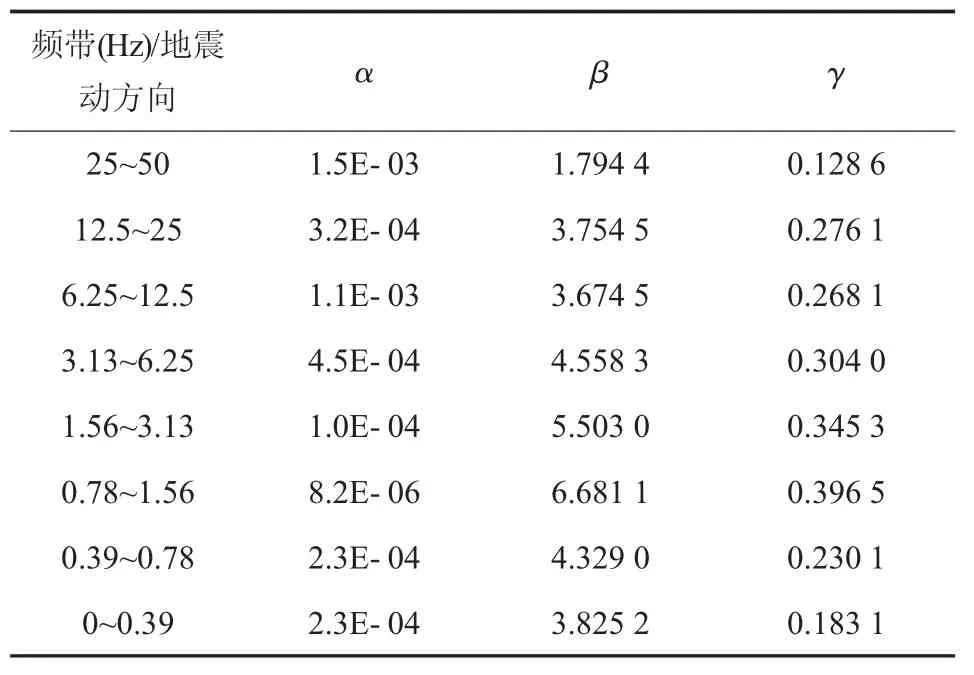
表2 由SMART1台网地震动信号E-45确定的Gamma模型参数

表3 由SMART-1台网地震动信号E-45确定的功率谱参数（胡聿贤谱n=6）

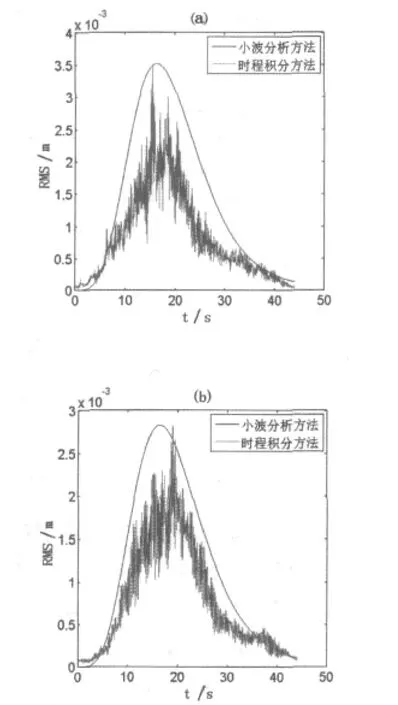
图4 一致地震动激动下连续刚桥左边跨及中跨跨中竖向总相对位移响应的瞬时均方根值对比图（a：左边跨，b：中跨）

通过以上的算例可以看出本文所提出的方法的计算结果与用时程分析方法计算统计的结果基本吻合，但是计算效率上却要大大优于时程分析方法，从而可以看出本文提出的方法在求解非一致地震响应时的优越性。

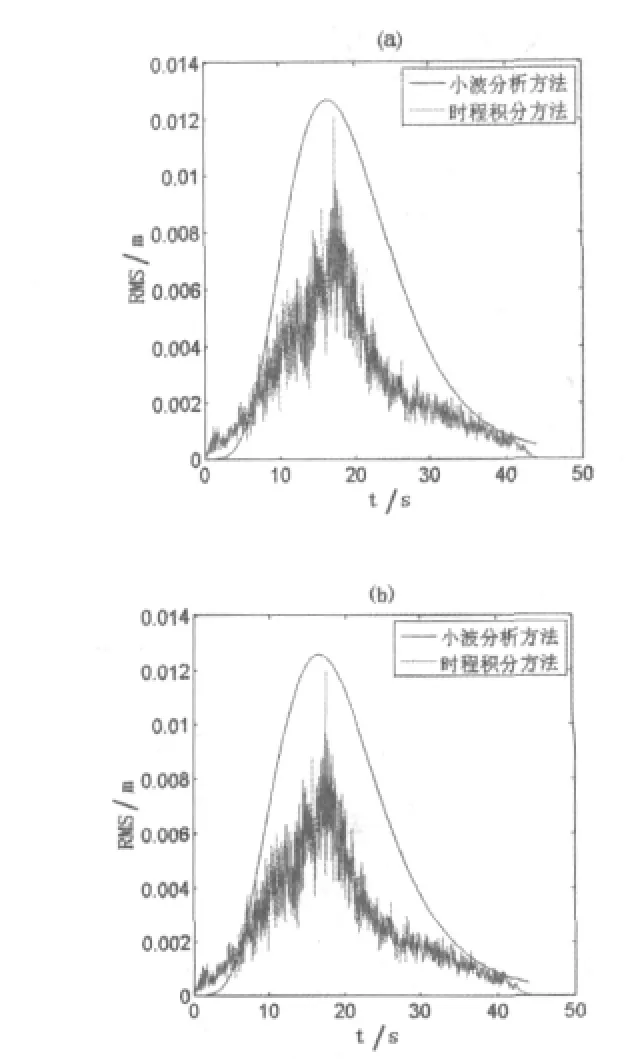
图5 一致地震动激动下连续刚桥1#墩及2#墩墩顶顺桥向总相对位移响应的瞬时均方根值对比图（a：#墩，b：2#墩）

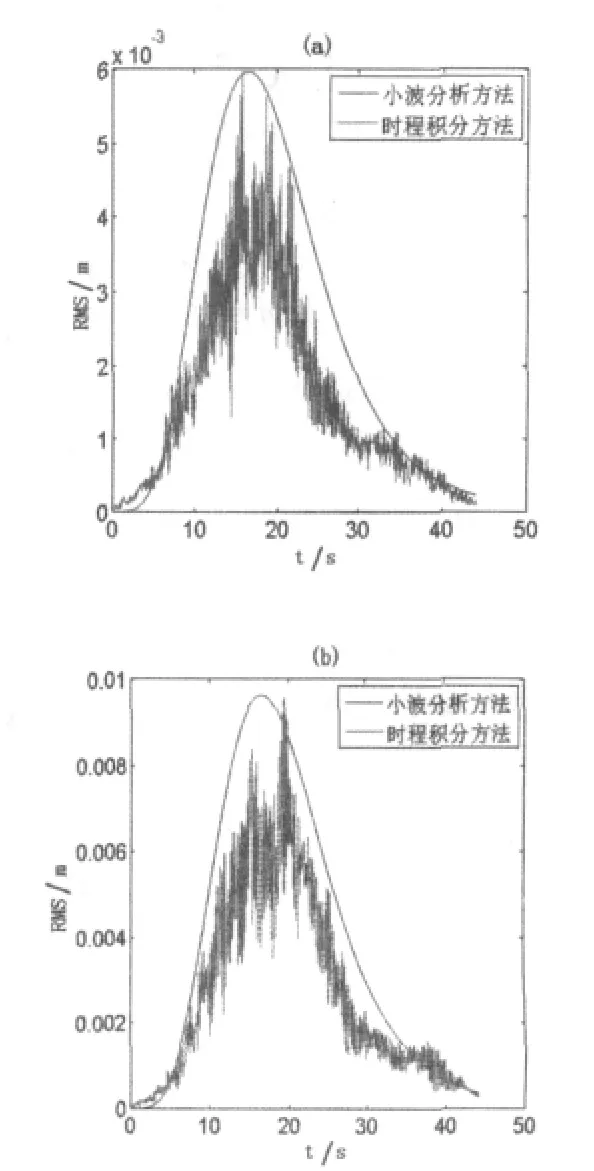
图6 非一致地震动激动下连续刚桥左边跨及中跨跨中竖向总相对位移响应的瞬时均方根值对比图（a：左边跨，b：中跨）

4 结论

本文利用小波理论首先提出了用于非一致激励的非平稳地震动荷载模型，该模型可以很方便地考虑地震动的行波效应，场地土特性及部分相干性的影响，其次推导了多自由度结构体系在非一致非平稳随机激励下响应的瞬时功率谱密度及响应的瞬时均方值的表达式，通过一座三跨连续刚构桥的算例验证了该方法的准确性。

[1]李建俊.随机地震响应分析的虚拟激励法[D].大连：大连理工大学，1994.

[2]Armen Der Kiureghian,A.Neuenhofer.Response Sepctrum Method for Multi-Support Seismic Excitations[J].Earthquake Eng.Struct.Dyn.,1992(21):713-740.

[3]Loh,C.H.,and Ku,B.D.,An efficient analysis of structural response for multiple-suppot seismic excitations[J].Eng.Struct.,1995,17(1):15-26.

[4]Lin J.H.,Shen W.P.,Williams F.M.Accurate High-Speed Computation of Non-Stationary Random Structure Response[J].Engineering Structures,1997,19(7):586-593.

[5]Kameda H.Evolutionary spectra of seismogram by multifilter[J].Engrg Mech Div，1975,101(6):787-801.

[6]Li Y,Kareem A.Simulation of multivariate nonstationary random processes by FFT.[J].Engrg Mech,1991,117(5):1037-1058.

[7]Li Y,Kareem A.Simulation of multivariate random processes:hybrid DFT and digital filtering approach[J].Engrg Mech,1993,119(5):1078-1098.

[8]Li Y,Kareem A.Simulation of multivariate nonstationary random processes:hybrid DFT and digital filtering approach [J].Engrg Mech,1997,123(12):1302-1310.

[9]Come J P,Peng B E.Fully non-stationary analytical earthquake ground motion model[J].Engrg Mech,1997(1):15-24.

[10]Deodatis G.Non-stationary stochastic vector processes:seismic ground motion applications[J].Probabilistic Engrg Mech,1996(11):149-168.

[11]M.B.Priestley.Evolutionary Spectra and Non-Stationary Processes,Journal of the Royal Statistical Society[J].Series B(Methodological),1965,27(2):204-237.

[12]Basu,B.and Gupta,V.K.Seismic response of SDOF system by wavelet modeling of nonstationary processes[J].Eng.Mech.,124(10):1142-1150.

[13]Clough R W,Penzien J.Dynamics of Structures[M].New York:McGraw-Hill Inc,1993

[14]G.Rodolfo Saragoni,Gary C.Hart.Simulation of artificial earthquakes [J] .Earthquake Engineering and Structural Dynamics,1974(2):249-267.