矩阵变换器过调制策略的研究

鲁 静，薛建设，蔡文君

（西安铁路职业技术学院机电工程系，陕西西安 710014）

1 引言

矩阵变换器是一种具有新颖拓扑结构的交—交型变换器，与传统的变频器相比，矩阵变换器以其能量可双向流动，功率因数可调，结构简单，控制自由度大等诸多优点［1］成为电力传动领域的新生军。

矩阵变换器概念的提出至今已有约30年，在调制策略、换流方式、器件开发等各项关键技术上均取得了很大的进步，但电压传输比低是其没有实现工业化生产最主要的原因［2-5］。因此，提高电压传输比的研究意义非常重大。

提高电压传输比可从硬件和软件两个方面来实现。硬件结构上，电路拓扑结构改变所增加的辅助电路会导致成本上升，修改不方便、并且增加了控制的难度。软件方面，调制策略控制方法相对简单，有利于数字化实现。因此利用调制策略来提高矩阵变换器的电压传输比成为近年来的研究热点。

Joachim Holtz［6］等在 1993 年提出在 VSI中将过调制区分为 0.907＜M＜0.952 和 0.952＜M＜1 两个区间，分别采用两种过调制策略，通过离线计算得到控制参数与给定参考的关系，并用在线查表的方式获得线性化的输入输出关系，很好地从过调制区平滑地过渡到最大基波输出。s.Bolognani［7］于1997年提出了单模过调制策略，即对过调制区域不进行划分，仅采用一种控制策略就可以获得电压的输入输出关系，简化了控制方法。但这两种调制策略均为非线性的过调制策略，占用内存空间大，不利于数字化实现。2000年B K Bose［8］在分析双模过调制原理的基础上，提出的基于人工神经网络（ANN）过调制策略，将其应用于矩阵变换器中。2003年 N V Nho［9］在分析双模过调制原理的基础上，提出了基于极限轨迹法的过调制策略。这两种方法均为线性的控制策略，计算方法简单，在硬件实现上具有明显的优势。下面一一介绍这几种过调制策略。

2 矩阵变换器的调制策略

将矩阵变换器等效为虚拟的整流器和虚拟的逆变器，可得到矩阵变换器的交—交直接变换关系，如图1、2所示。采用这样的等效结构可以充分利用成熟的PWM控制技术，同时可得到实际变换器的开关控制。

在逆变级中采用过调制策略来提高矩阵变换器的电压传输比，下面介绍矩阵变换器的过调制策略。

3 矩阵变换器的过调制策略

3.1 双模过调制策略

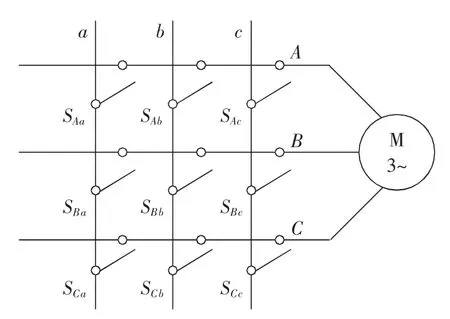
图1 三相-三相矩阵变换器拓扑结构图

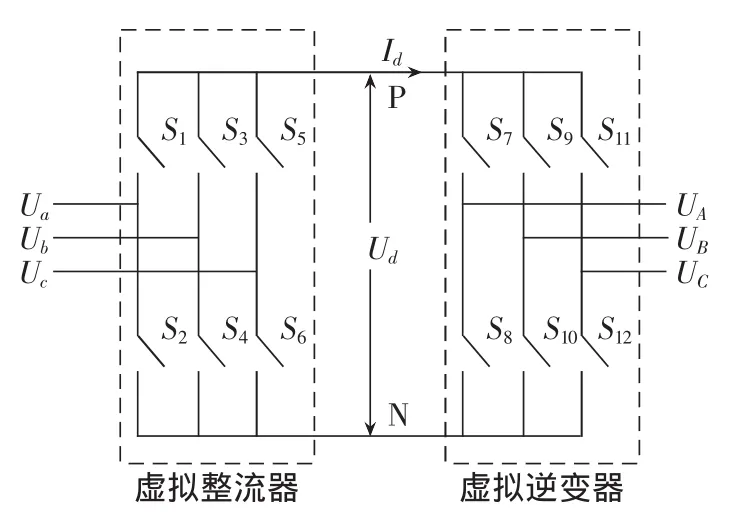
图2 矩阵变换器等效交-直-交结构图

Joachim Holtz等提出在VSI中将过调制区分为 0.907＜M＜0.952 和 0.952＜M＜1 两个区间，分别采用两种过调制策略，通过离线计算得到控制参数与给定参考的关系，并用在线查表的方式获得线性化的输入输出关系，很好地从过调制区平滑地过渡到最大基波输出。

下面以第一扇区为例来说明过调制双模控制策略的原理。

（1）过调制模式I

如图3所示为电压空间矢量过调制模式I。图3中，U＊为电压参考矢量轨迹，Up＊为实际输出轨迹，据图描述过调制模式1的工作原理如下。

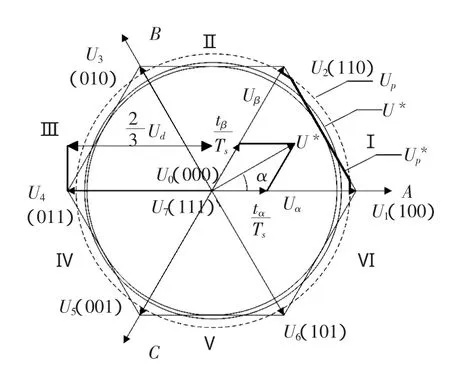
图3 电压空间矢量过调制模式I

当U＊超出正六边形范围时，通过减小U＊的幅值使U＊的终点落在正六边形上；当U＊处于正六边形之内时，提高其幅值到Up以补偿U＊在超出正六边形范围时无法输出的电压损失，最后得到实际的输出电压轨迹Up＊为：

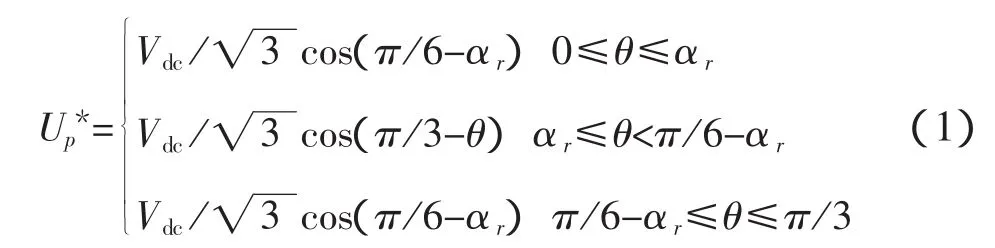
图4 SVPWM过调制模式II

（2）过调制模式II

如图4所示为SVPWM过调制模式II。

过调制模式II的工作原理描述如下：

当θ在保持角αh内时，输出电压矢量保持在六边形顶点，当θ大于保持角αh时，输出电压矢量沿着六边形的边。由此可得输出电压矢量Up＊的相角 θ′为：

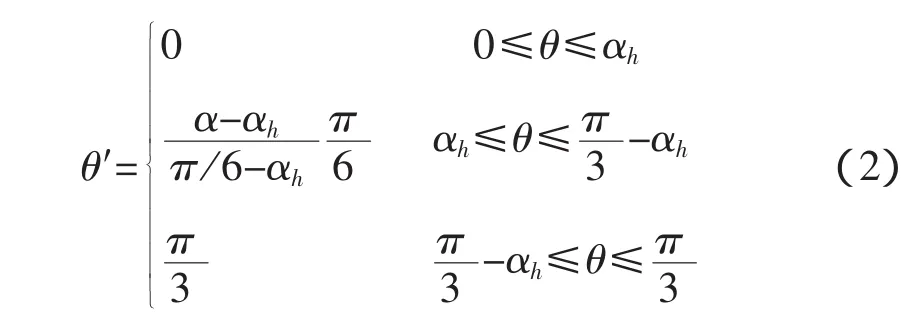
此策略的特点是控制策略非常复杂，电压传输比与控制参数、开关占空比计算非线性关系使得计算异常复杂，控制精度低。

3.2 单模过调制策略

s.Bolognani［i］在 1997 年发表的论文中提出在VSI中不将过调制区进行划分，仅采用一种控制策略就可以使得输出基波平滑地过渡到最大的六阶梯波，简化了控制方法，对系统资源紧张的应用是很有价值的。也就是常说的单模控制策略。

下面以第一扇区为例来说明过调制单模控制策略的原理。如图5所示为SVPWM单模过调制。

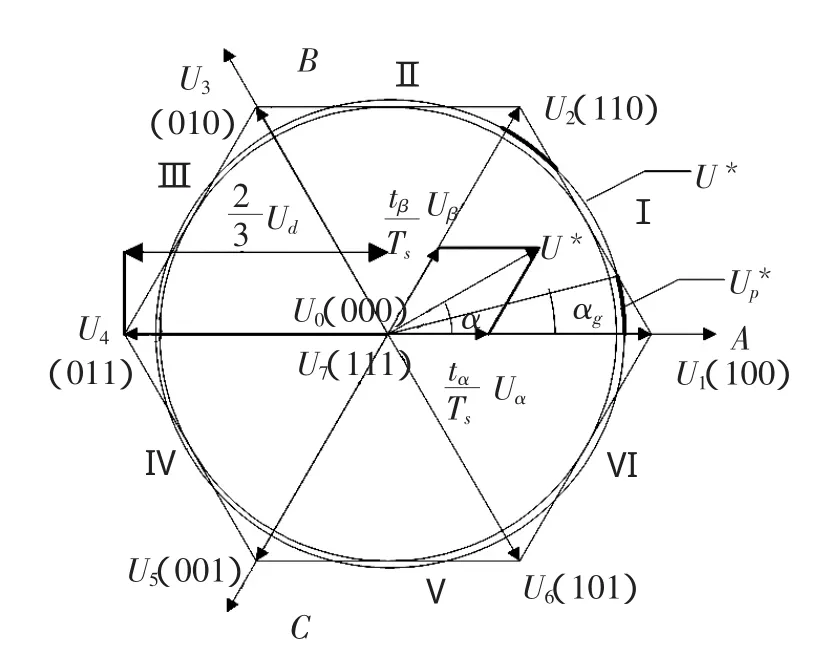
图5 SVPWM单模过调制

实际输出电压矢量为：

当θ角在0和保持角αg之间时，输出角θ′等于 θ；当 θ角在 αg和，输出角 θ′等于 αg；当角 θ在时，输出角 θ′等于当 θ角在时，输出角 θ′等于 θ。

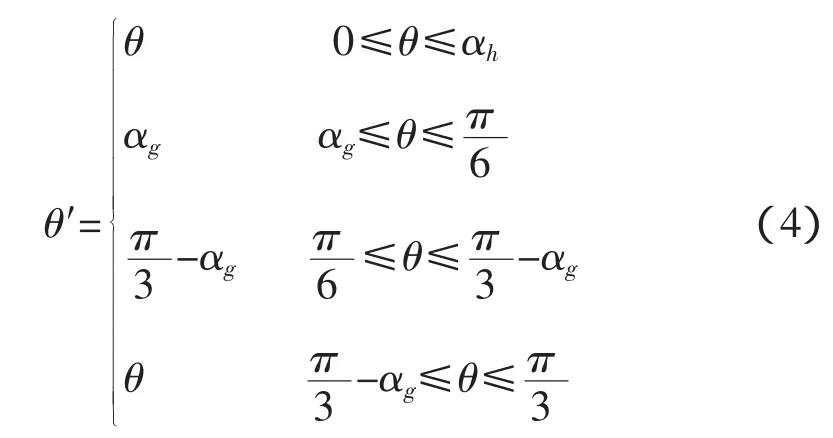
此策略的特点是控制策略简单，不用划分区间，但谐波含量大，也没有解决电压传输比与控制参数、开关占空比计算的非线性关系。

3.3 基于极限轨迹法的过调制策略

如图6所示为极限轨迹法调制原理图。假设在正六边形内有3个有效矢量Ua、Ub和U，则矢量U可以表示为Ua与Ub的线性组合。

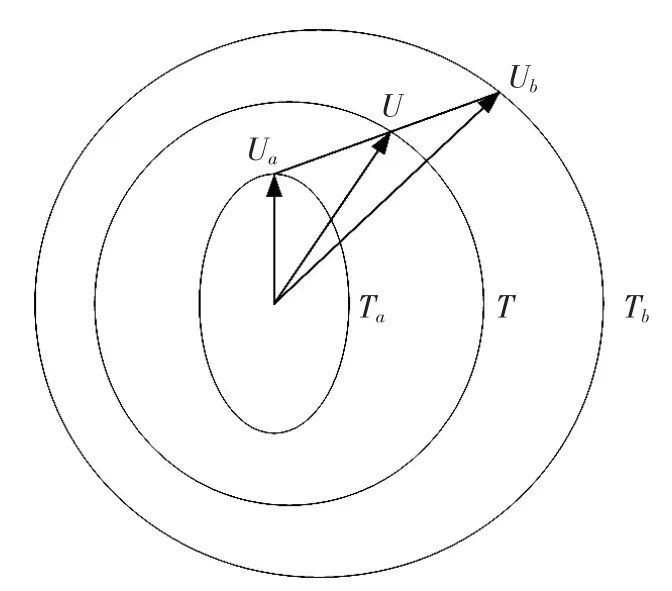
图6 极限轨迹法调制原理

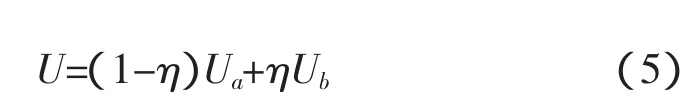
当η在0～1之间变化时，矢量U从Ua变到Ub。当矢量Ua和Ub以各自的幅值为半径旋转时，合成矢量U也以自己的幅值为半径旋转。合成矢量 U 的基波幅值 U1［8］为：

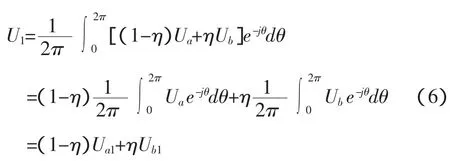
式中：Ua1、Ub1为 Ua和 Ub的基波幅值。

由此可知，任意一个给定的矢量，根据调制系数的不同，可以看作是两个有效矢量共同作用的结果，这两个有效矢量基波幅值的和等于给定矢量的基波幅值。因此，对给定矢量的调制，就转化为对其两个分量的分别调制。

基于极限轨迹法的过调制策略，实现算法简单，不需要计算控制角，直接由调制系数计算出开关的占空比，通过线性计算来控制输出电压，计算的精度更高。

3.4 基于人工神经网络的过调制策略

2000年B K Bose在分析双模过调制原理的基础上，提出了基于人工神经网络（ANN）的过调制策略。过调制策略图如图7所示。采用多个简单的前向ANN结构模型及固定权值和有监督训练两种策略，对过调制的控制算法进行了研究，得到一种基于ANN的过调制策略。由于采用了多个子网络结构，使得任务的复杂程度分散、降低，ANN的快速并行处理能力和学习能力使得计算时间大大降低。设计中涉及到的网络训练样本数量很小，训练时间短，收敛速度快。

图7 基于ANN的双模过调制策略结构图

本策略在仿真试验中验证了谐波成分较小，为矩阵变换器的过调制策略提供了一种新思路、新方法。

4 结论

本文总结了矩阵变换器的几种过调制策略，同时分析了各自的优点及缺点。在比较中发现，基于人工神经网络的过调制策略为最优的过调制算法，为硬件实验提供了理论依据。

［1］孙 凯，周大宁，梅 杨.矩阵变换器技术及其应用［M］.北京：机械工业出版社，2007.

［2］郭有贵，喻寿益，朱建林.交-交矩阵变换器电压传输比的仿真研究［J］.系统仿真学报，2006，18（12）：3482-3485.

［3］陈罗湘，朱建林.采用过调制技术的矩阵变换器应用技术研究［J］.电力自动化设备，2006，26（8）：23-26.

［4］张艳芳，林 飞，马志文等.两种SVPWM过调制方法的比较研究［J］.北京交通大学学报，2005，29（2）：39-43.

［5］郭有贵.交-交矩阵变换器控制策略及提高电压传输比研究［D］.长沙：中南大学，2005.

［6］J Holtz，W Lotzkat，A Khambadkone.On Continuous Control of PWM Inverters in the Overmodulation Range including the Six-Step Mode［J］.IEEE Trans.PE，1992，（8）：546-553.

［7］S Bolognani，M Zigliotto.Novel Digital Continuous Control of SVM Inverters in the Overmodulation Range［J］.IEEE Trans.On IA，1997，33（2）：525-530.

［8］J O P Pinto，Bose B K，Luiz Eduardo Borges da Silva，Marian P Kazmierkowski.A Neural Network Based Space-Vector PWM Controller for Voltage Fed Inverter Induction Motor Drive［J］.IEEE Trans Ind Appl，2000，36（6），1628-1636.

［9］Nho N V.Two-Mode Overmodulation in Two-Level Voltage Source Inverter Using Principle Control between Limit Trajectorie［C］.Proceedings of PEDS 2003，Singapore，2003：1274-1279.