数字锁相技术在APFC电压采样中的应用

刘 攀，高艳霞，杨郑浩

（上海大学，上海 200072）

1 引言

APFC（有源功率因数校正）技术采用全控开关器件构成开关电路对输入电流波形进行控制，使其成为与电源电压同相位的正弦波，彻底解决整流电路的谐波污染和功率因数低的问题。采用APFC技术能有效降低谐波含量，提高功率因数（功率因数能高达0.995），满足严格的谐波标准，近年来得到广泛的应用。单相有源功率因数校正电路结构简单，克服了三相有源功率因数校正电路结构和控制复杂的缺点，电路易于实现，可靠性较高，广泛应用于0.5-3kW范围内单相输入开关电源［1］。

传统的APFC控制电路容易受到外电路的影响，电流环给定并非纯正弦波，会导致功率因数降低，引入单相数字锁相环技术对输入电压进行采样以减小电流失真度，实现功率因数调节。

2 单相功率因数校正电路

基于平均电流法控制的单相APFC电路如图1所示，主电路实际上由二极管整流电路和升压斩波电路组成，控制电路采用双闭环控制结构。外环电压环以输入整流电压和输出电压误差放大信号的乘积作为电流基准，内环电流环调节输入电流平均值，使其与输入整流电压同相位且接近正弦波，校正功率因数［2］。

电流反馈网络的采样信号是Boost变换器的电感电流，正比于输入电流的电流采样信号与电流基准信号比较以后，其高频分量的变化通过电流误差放大器被平均化处理，放大后的平均电流误差经信号处理（平均电流误差与锯齿波进行比较）转换为PWM脉冲，控制开关管的开通和关断。S导通时，电感电流线性上升。当输入电流采样信号与参考电流波形相交时，控制器控制S关断，此时电感的自感电势使二极管导通，储能电感L通过二极管D对电容C进行充电，电感电流下降。通过对电感电流进行采样和控制，使电感电流与输入电压同相位的正弦参考信号成正比，从而达到功率因数校正的目的［3］。

图1 平均电流法控制的单相APFC原理框图

Boost型APFC电路的状态平均等效电路如图2（a）所示，将电路中的电压和电流用向量表示，可以得到图2（b）所示的向量图。由于输入电压是交流电压整流后得到的直流脉动波形，是以［0，π］为周期重复的，因此输入电压表达式定义在［0，π］区间上。

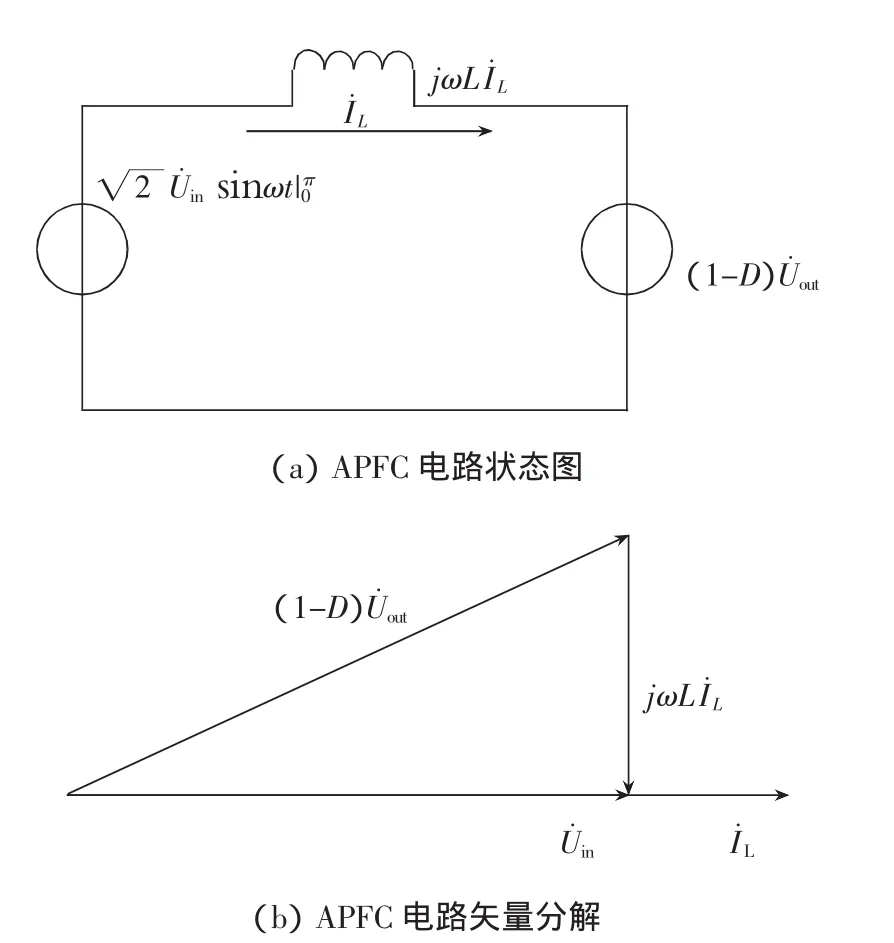
图2 APFC电路状态及矢量图

U˙in为输入电压相量，I˙L为电感电流相量，电感两端的电压jωLI˙L超前电感电流90°，只要选择合适的占空比控制规律，使（1-D）U˙out-U˙in＝jωLI˙L按正弦规律变化，且相位比U˙in超前90°，就可以实现电感电流对输入电压的跟踪。

3 APFC电流波形畸变的原因

电网中理想的输入电压与输入电流同相位，均为正弦波，分别为Iin_rmssin（ωt）。

其中uin经过整流桥整流后得到直流电压，Uin_rms为输入电压的有效值，ω为输入电压的角频率。若电压、电流不同相位，设输入电流为Iin_rmssin（ωt+θ），θ为输入电流滞后于输入电压的滞后角。对输入电流进行求导得到所需要的电流上升斜率：

变换器在输入电压过零附近时占空比值达到最大［4］，此时输入电压直接加在电感两端（即电感电压等于输入电压），则变换器提供的电感电流上升斜率为：

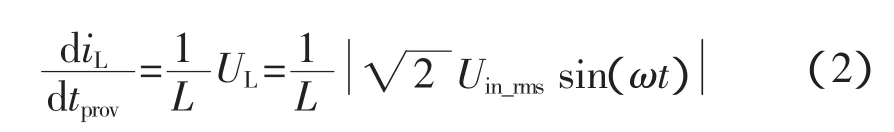
其中UL为电感电压，电感电流等于输入电流。变换器在输入电压过零时，电感电流的上升率很小，电感电流很难跟踪上给定的基准电流，因此输入电流发生畸变。

由式（1）和式（2）可以得出，电网角频率 ω、输入电流滞后角θ、电感L的大小及输入电压的波形都将对电压过零时电流的畸变产生影响。其中电感越小，变换器提供的上升斜率越大［5］，电流畸变越严重。同时由于线路中耦合寄生感抗的影响，采样输入到AD端的输入电压并非正弦基波，若直接采用这种非正弦电压作为输入电压，将导致电流环给定的电流基准为非正弦基波，影响PF值校正。

本设计引入数字锁相环技术以滤除电网电压中的各次谐波的干扰，抑制输入电流过零点畸变，进一步提高功率因数。

4 数字锁相环与滤波器设计

4.1 数字锁相环建模

利用单相数字锁相环对输入市电进行锁相，将锁相后的电压信号作为电压相位给定值提供给电流环，以减少最高处的电压畸变。单相锁相环采用类似三相电压锁相环的方法，通过构造虚拟dq轴，PARK变换和应用数字滤波器，使电流环的电流基准信号跟随输入电压变化。

图3所示为静止坐标轴与旋转坐标轴的关系。

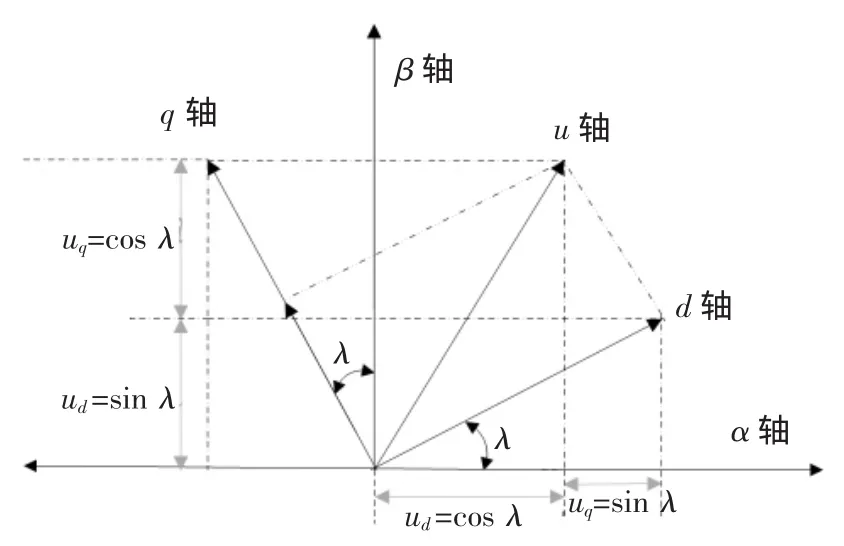
图3 静止／旋转坐标轴空间关系

由上图可以得出

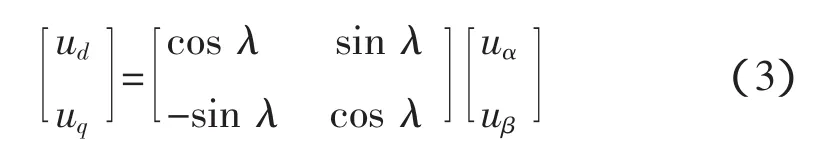
（其中α、β为静止坐标轴，d、q为旋转坐标轴，λ为两坐标轴相位角）

将包含各次谐波的单相市电分解为基波与各相谐波之和，即

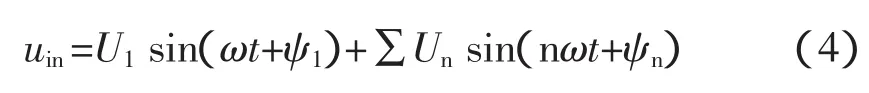
系统角频率为ω，且dq旋转坐标系同步旋转。若基波相电压在静止坐标轴上投影为uα＝U1cos（ωt+ψ1）和 uβ＝U1sin（ωt+ψ1），则其在 dq 旋转坐标系上的投影分别为 ud＝U1cos ψ1和 uq＝U1sin ψ1。

令所检测的输入电压在当前静止坐标系轴上的分量分别为：

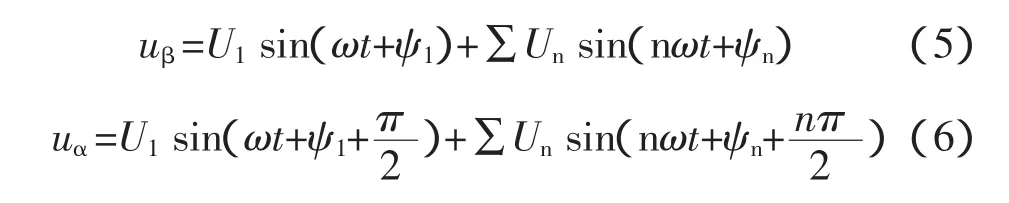
将式（5）、（6）代入式（3），经过 dq变换后得到：

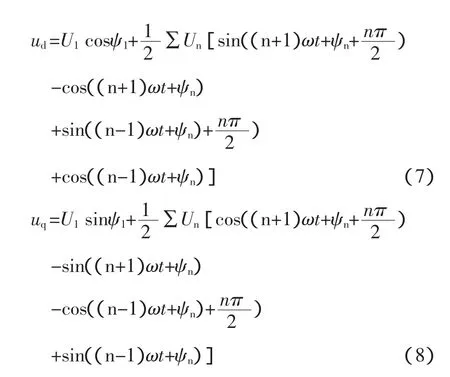
经高频滤波后，得到两个直流分量ud和uq，即ud＝U1cos ψ1和 uq＝U1sin ψ1。

设此处实际输入角频率为ω1，输出角频率为ω，则整个系统可以表示为：

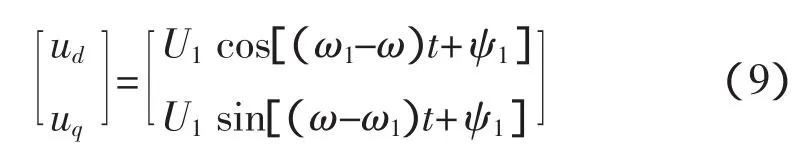
当输出角频率ω大于输入角频率ω1，通过PI调节使ω1-ω＝0，此时uq为直流量，直流量的输入可以使输出频率加大，从而使输出相位得到调整。当ω1≠ω，uq为变化的交流量，此时系统进入角频率调整阶段，如此反复直到输入信号与锁相环完全同步。

通过Matlab／Simulink对上述模型进行仿真，图4所示为仿真模型，图5所示为仿真波形。由仿真波形可以看出，利用锁相环可以对输入电压完成锁相，在仿真开始时（第一个周期时），锁相电压并不能完全跟随实际输入电压，随着仿真的进行，在第二周期时，锁相电压已经能够完全完成对实际输入电压的锁相。仿真结果表明利用该方法能够有效地锁住输入电压的相位。

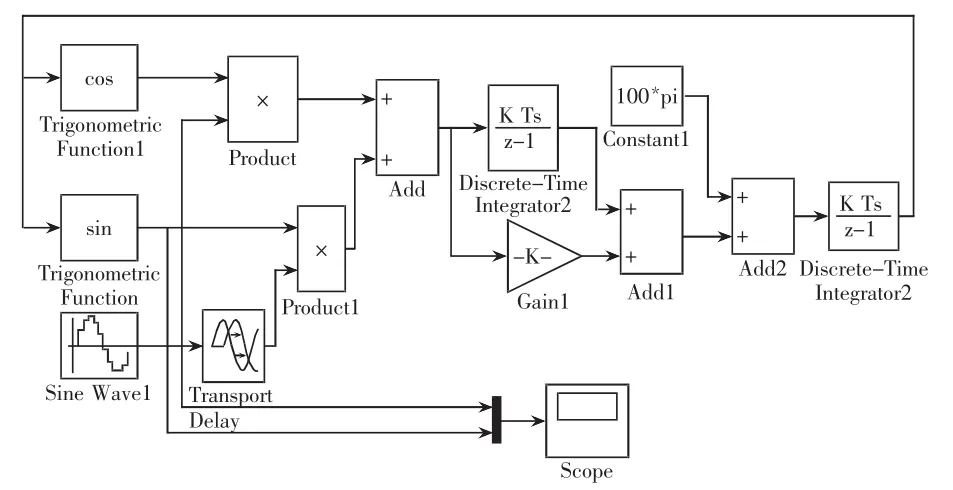
图4 基于Simulink的数字锁相环建模

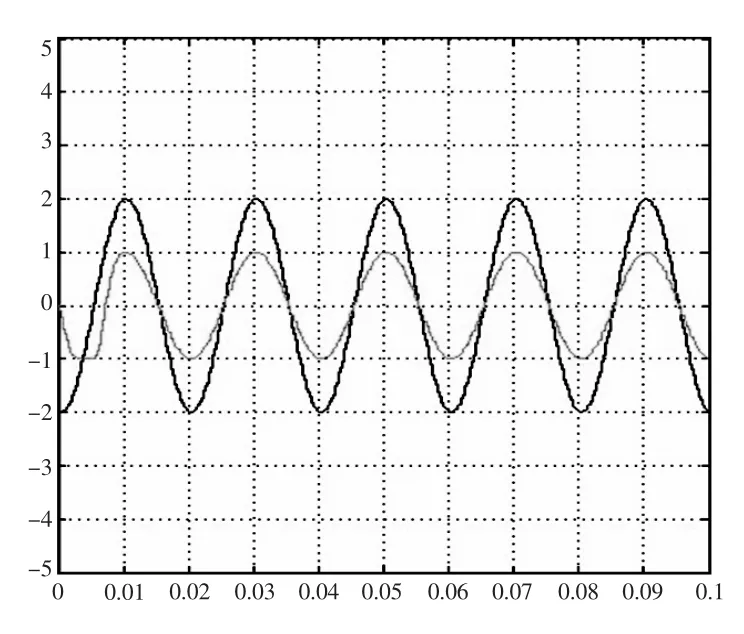
图5 基于Simulink数字锁相环仿真波形

4.2 数字滤波器设计

在锁相环运算中，需要采用数字滤波器以滤除输入电压中的谐波分量。常用的低通数字滤波器采用一阶结构，该方法容易造成相位延迟，且截止频率越低，相位延迟越严重。本设计中的数字锁相环需要滤除高于基波分量的各次谐波，市电基波频率为50Hz，若使用一阶低通滤波会造成较大的相位延迟，不能满足系统要求。

采用巴特沃斯滤波器作为uq的数字滤波器，巴特沃斯滤波的特点是通频带的频率响应曲线平滑，并且能够保证衰减速度较快，效果优于传统的一阶低通滤波器。

为了方便数字巴特沃斯滤波器的设计，采用二阶滤波设计方法，其转移函数为：

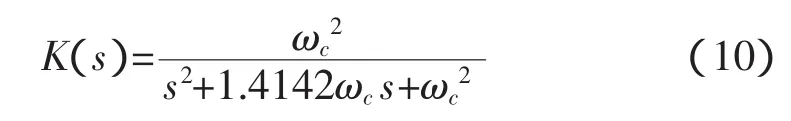
截止频率为30Hz时计算得到截止角频率为：

代入式（10）得：

取采样频率为25.6kHz，对上式进行双线性变换得到离散表达式：

即为：

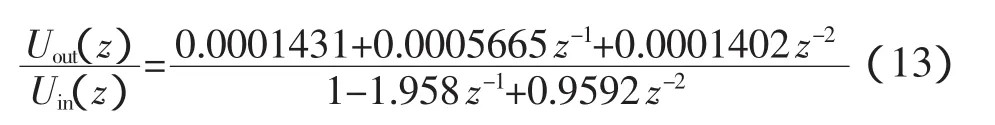
整理得到：

5 数字锁相环实验与分析

5.1 硬件设计

系统控制器采用TMS320F2812，该芯片A／D输入为0-3.3V的电压信号，故需将采样得到的电网交流电压信号转化为0-3.3V的电压信号。电压转换可以通过在采样信号上叠加1.65V直流分量来实现，硬件电路如图6所示。

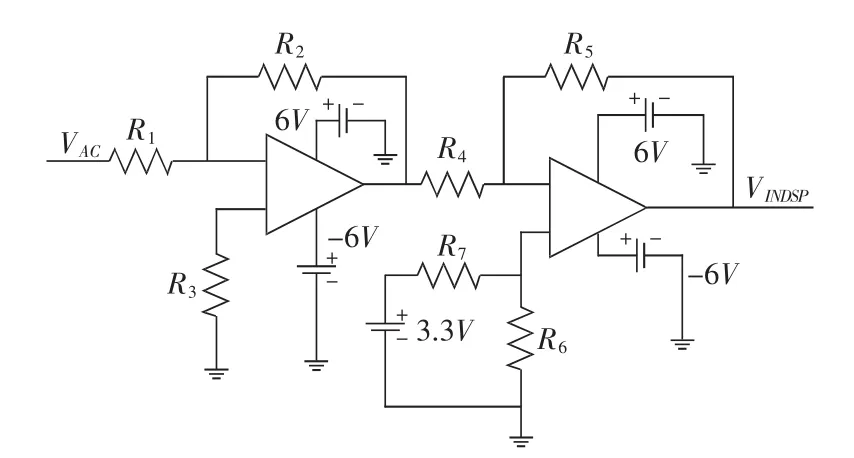
图6 交流电压采样电路图

由图6得到输入DSP2812的AD检测口电压为：

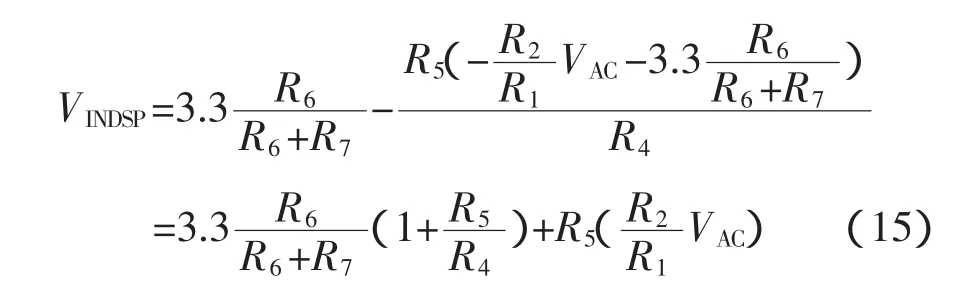
取 R1、R3、R5及 R6为 10kΩ，R2、R4、R7为20kΩ，则交流信号波形与经过处理的采样波形如图7所示，实验波形符合上式计算结果。

将采样处理后的电压信号在数字信号处理器内完成异或功能，将第一位符号位进行逻辑变换，转换为交流信号值存储在寄存器中，处理原理如图8所示。

图7 交流电压信号采样波形

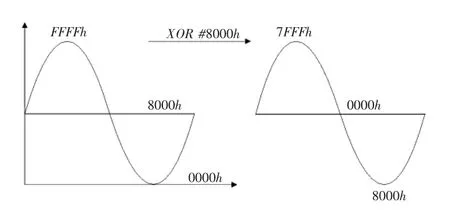
图8 交直流信号在DSP内部逻辑运算图

5.2 软件设计

采用TMS320F2812数字信号处理器实现数字锁相环，在RAM中建立一个512个字节的数组用于存放数据。设定采样电网电压为正弦基波，将其保存在RAM中，并且将指针后移128位作为余弦量。将反馈的相位信号进行Q格式变换，以加快运算速度，同时根据设计的巴特沃斯数字滤波器完成对高频分量进行滤除。图9所示为数字锁相环的软件设计流程。

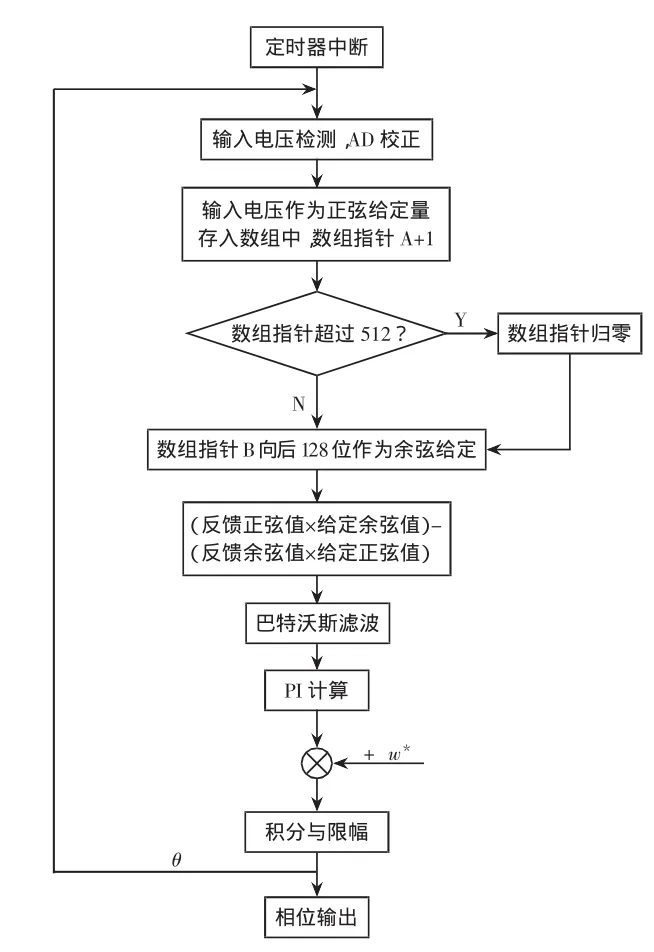
图9 数字锁相环软件流程图

5.3 实验结果

采用数字信号处理器完成数字锁相环设计，完成对输入电压的锁相，从DSP编译环境Watch Window中观察实验波形如图10、11所示。图10为未加入锁相环时输入电压的波形，由于寄生参数及采样偏差的影响，采样得到的输入电压中存在谐波影响。图11为加入锁相环后的电压采样波形，实验结果表明数字锁相环明显改善了输入电压波形的畸变。

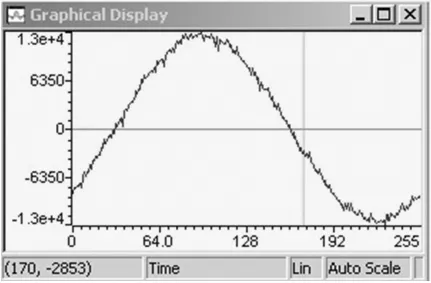
图10 未加入锁相环时输入电压的波形

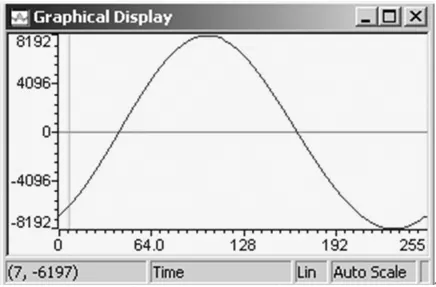
图11 加入锁相环后的电压采样波形

6 结论

在单相APFC原理基础上分析了APFC电流畸变的原因，提出利用数字信号处理器TMS320F2812构建单相数字锁相环，通过对输入市电电压完成锁相以克服耦合寄生电感对功率因数校正的影响，解决输入电压过零时输入电流过零畸变及峰值畸变问题。通过旋转坐标系完成对数字锁相环的建模，设计数字巴特沃斯滤波器滤除轴分量的高频谐波，克服一阶滤波器的相位延迟的不足。最后仿真和实验结果表明利用数字锁相环可以有效的完成对输入电压的锁相，实现给定基准电流信号跟随输入电压，实现功率因数校正。

［1］杨 旭，裴云庆，王兆安.开关电源技术［M］.北京：机械工业出版社，2004.

［2］魏 滢，刘 辉.单相APFC数字控制的实现［J］.电源世界，2010，（1）：37-39.

［3］陈庆生.APFC技术在通信电源中的应用［J］.电源世界，2004，10：33-35.

［4］范 凯，谢少军.单相PFC变换器的电流过零畸变问题研究［J］.电力电子技术，2009，43（4）：18-20.

［5］王菁，王毅，刘志宇.数字APFC的电流采样算法改进［J］.电力电子技术，2009，43（5）：10-14.