有关中国剩余定理在多个素数的RSA解密运算中的加速公式的论证以及加速效率的估算
刘 承 彬, 耿 也, 舒 奎, 高 真 香 子
( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )
0 引 言
RSA加密算法是第一个既能用于数据加密也能用于数字签名的算法。RSA算法基于单向陷门函数原理,依赖于大数因数分解的困难性。因此,基于大整数分解问题的RSA算法是目前实际应用最广泛的公钥密码算法。
随着科学技术的发展,为保证RSA算法有足够的安全性,RSA算法需要的密钥长度不断增加,明显降低了加密/解密的效率。出于安全性考虑,一般要求密钥长度在1 024~2 048 bp[1]。因为运用RSA算法对数据进行加解密运算需要进行大量模幂运算,密钥越复杂,RSA处理数据的速度越低,由于中国剩余定理对于提高模幂运算效率有显著提升,因而与RSA一起使用。
1 使用中国剩余定理对RSA解密算法的加速公式推论
1.1 RSA算法的基本阐述[2]
步骤1采用Montgomery算法优化后的Miller Rabin算法[3]取2个互质的素数p和q,令N=pq;Φ(N)=(p-1)(q-1)。
步骤2取与Φ(N)互质的整数e,且1 步骤3加密过程:C=MemodN;解密过程:M=CdmodN。 (1)每个素数都要足够大;(2)每个素数均为强素数;(3)各个素数之差要大,差多个位以上;(4)各个素数与1求差之后新形成的各个数的最大公因子要小。 采用Montgomery算法优化后的Miller Rabin算法,取n个互质的素数p1,p2,p3,…,pn,令N=p1p2p3…pn;Φ(N)=(p1-1)(p2-1)(p3-1)…(pn-1)。 加密过程采用原始的加密方式:取与Φ(N)互质的整数e,且1 对任意给定的数M,加密后的数C=MemodN。解密过程采用中国剩余定理优化的解密方式。对于同余方程组: M≡Mp1modp1,M≡Mp2modp2,M≡Mp3modp3,…,M≡Mpnmodpn,模N有唯一解,解为M≡(Mp1M1y1+Mp2M2y2+Mp3M3y3+…+MpnMnyn)modN。式中, M1=p2p3p4…pn, M2=p1p3p4…pn, M3=p1p2p4…pn, ⋮ Mk=p1p2p3…pk-1pk+1…pn,…, Mn=p1p2p3…pn-1, M1y1≡1modp1,M2y2≡1modp2, M3y3≡1modp3,…,Mnyn≡1modpn。 由费马小定理:令p为素数,对任何不能为p整除的数A,恒满足Ap-1≡1modp,可得:Ap-2≡A-1modp,所以 modN。 由于M≡Mp1modp1,M≡Mp2modp2,…,M≡Mpnmodpn[4],所以Mp1≡Mmodp1≡(CdmodN)modp1≡Cdmodp1。 由费马小定理推论:令p为素数,对任何不能为p整除的数A,且有n=mmod(p-1),则An≡Ammodp,可得: Cdmodp1=Cdmod(p1-1)modp1 令dp1=dmod(p1-1),则Mp1=Cdp1modp1;其中dp1可看作采用中国剩余定理简化后新的n个私钥中的1个。 同理,Mp2=Cdp2modp2,…,Mpn=Cdpnmodpn;且产生新的私钥dp2,dp3,…,dpn。 又由Cdp1modp1=(Cmodp1)dp1modp1,令Cp1=Cmodp1,即Mp1=Cp1dp1modp1; 同理可得Mp2=Cp2dp2modp2,…,Mpn=Cpndpnmodpn。 对于采用中国剩余定理简化的RSA解密算法可分解为4个步骤执行: 步骤1计算dp1=dmod(p1-1),dp2=dmod(p2-1),…,dpn=dmod(pn-1); 步骤2计算Cp1=Cmodp1,Cp2=Cmodp2,…,Cpn=Cmodpn; 步骤3计算Mp1=Cp1dp1modp1,Mp2=Cp2dp2modp2,…,Mpn=Cpndpnmodpn; 步骤4计算 modp1p2…pn 注:此公式仅适用于解密算法。 通过比较可以发现,虽然计算的步骤增多,但是每一步需要的模幂运算大量减少,从而大大降低运算的复杂程度。 下面分别对4~6个素数的情况通过计算机程序来验证该公式的正确性,如图1~3所示。 图1 4个素数时基于中国剩余定理加速后采用C++实现的结果 图2 5个素数时基于中国剩余定理加速后采用C++实现的结果 图3 6个素数时基于中国剩余定理加速后采用C++实现的结果 采用Montgomery算法优化后的Miller Rabin算法取n个互质的素数,假设每个素数的二进制长度均为k/nbp,则对于N和d的二进制长度我们可认为是kbp。 没有采用中国剩余定理加速的RSA解密算法M=CdmodN,实际操作可估算为k3次位操作(其中忽略2进制字节长度相差过大的数的计算)。 modp1p2…pn 其中主要的计算均集中在Mp1,Mp2,Mp3,…,Mpn,以及(p2p3p4…pn)p1-1,(p1p3p4…pn)p2-1,(p1p2p4…pn)p3-1,…,(p1p2p3…pn-1)pn-1中,由Mp1=Cp1dp1modp1,Cp1=Cmodp1,dp1=dmod(p1-1)可估算Mp1(p2p3p4…pn)p1-1共采用(n-1)2k3/n3+k3/n3次位操作[5],即(n2-2n+2)k3/n3次位操作(其中忽略2进制字节长度相差过大的数的计算)。若采用并行算法同时计算,则可得计算效率为原先n3/(n2-2n+2)倍。 4个素数时的效率提升:Mp(qrs)p-1的主要操作为10k3/64次位操作。采用并行算法后效率提升64/10倍,符合公式的计算。 5个素数时的效率提升:Mp(qrst)p-1的主要操作为17k3/125次位操作。采用并行算法后效率提升125/17倍,符合公式的计算。 6个素数时的效率提升:Mp(qrstu)p-1的主要操作为26k3/216次位操作。采用并行算法后效率提升216/26倍,符合公式的计算。 由式n3/n2-2n+2可知,随着n的增加,采用中国剩余定理的加速效果越明显。 通过选择多个素数的RSA算法,首先可以在选择大素数时适当减小素数位数,从而在根本上减少计算量。在解密过程中,采用中国剩余定理将私钥d转换成多个dx的运算,进一步减少d的位数,再一次减少计算量。 通过分析中国剩余定理, 提出了适合于计算多素数RSA算法中数据解密部分的计算公式,并采用并行方式来处理, 简化了模幂运算复杂的解密过程,显著提高了数据处理速度。由于“组成各种长度的模究竟多少个素数才合适”[6]这个论题仍在研究中,所以同时给出了采用中国剩余定理加速后的效率提升的估算公式。结合素数个数增加时的计算复杂度和采用中国剩余定理加速后的效率提升可确定出素数个数的范围。本文的不足之处在于只针对了解密算法的研究,没有从理论上证实破译RSA的难度和大数分解难度相等价,在以后的研究中将作为主要研究方向。 [1] 饶进平,冯国登. 一种高效率的RSA模幂算法的研究[J].计算机工程与应用, 2003(9):76-77, 121. [2] ABOUD S J, AL-FAYOUMI M A, Al-FAYOUMI M. An efficient RSA public key encryption scheme[C]. Washington DC:Fifth International Conference on Information Technology: New Generations, 2008:127-130. [3] 叶建龙. RSA加密中大素数的生成方法及其改进[J]. 廊坊师范学院学报:自然科学版, 2010, 10(2):55-57. [4] 徐进. 三素数RSA算法的快速实现[J]. 计算机工程与应用, 2006, 42(11):57-58. [5] 施月玲,夏涛,丁宏. 利用中国剩余定理改进大数模平方计算研究[J]. 杭州电子科技大学学报, 2007, 27(1):42-45. [6] BURNETT S, PAINE S. RSA security′s official guide to cryptography[M]. New York: McGraw-Hill Education, 2001:89-96.1.2 使用中国剩余定理简化n素数RSA解密算法时素数的选取原则
1.3 使用中国剩余定理对n素数RSA解密算法的简化
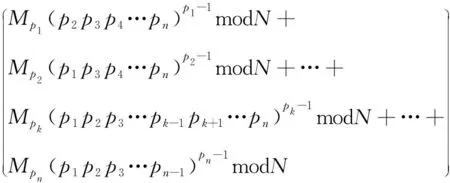
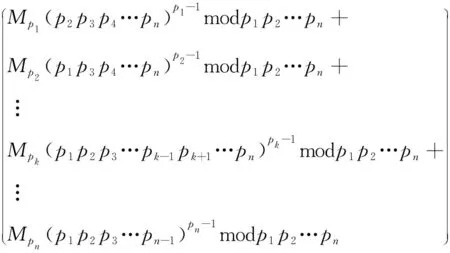
1.4 使用中国剩余定理对4素数和更多素数情况下的RSA解密算法的简化程序验证



2 采用中国剩余定理对RSA解密算法加速时的效率估算
2.1 使用中国剩余定理对n素数RSA解密算法的简化时的效率提升的公式推导
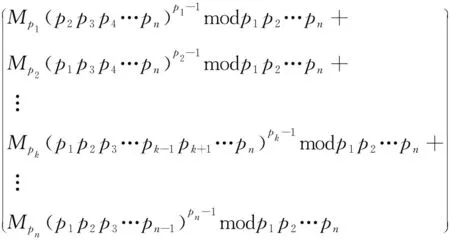
2.2 使用中国剩余定理对多素数时RSA解密算法的简化时的效率的提升的验证
3 结 论

