基于自适应小波系数的纸币数字水印的实现

袁 庆 玲, 里 红 杰, 陶 学 恒

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

纸币作为主要的货币流通手段在人们的生活中承担着重要的角色,但各种各样的假钞也同时出现在人们的生活中,给人们的生活增加了不和谐音符[1-2]。随着纸币制造技术的提高以及验钞机的不断更新换代,假钞不但没有减少反而增多,有的甚至可以躲过验钞装置的检验,流通于市场。据警方透露,2008年末我国检获假人民币上亿元,而且这批假币在验钞机里验不出“真身”。

目前各国的钞票防伪技术主要集中于特殊纸张和防伪制版及印刷[3]。随着印刷技术的不断普及和世界知识的共享,人们对制造纸币的流程和技术不断熟悉,制造假钞的工艺越来越被人熟知,因此必须在纸币的制作和检测方面加入新的技术。

数字水印技术具有如下3个特点:

(1)安全性:信息安全,难以篡改或伪造。当原内容发生变化时,数字水印也相应变化,从而可以检测原始数据的变更；数字水印同样对重复添加有强抵抗性。

(2)隐蔽性:不可知觉,而且不影响被保护数据的正常使用；不会降质。

(3)鲁棒性:在经历多种无意或有意的信号处理过程后,数字水印仍能保持部分完整性并能被准确鉴别。

本实验将数字水印技术应用到纸币防伪来提高纸币的伪造难度,从而提高纸币的安全性。

纵观近几年有关验钞机的专利,中国的发明专利中只有鲍东山[3]的专利将纸币数字化处理分析,其他都是在努力提高组成验钞机的各个组件的精度。鲍东山使用Intel 586-133作为微处理器,消耗功耗大,由于其功能需要外围扩展,一定程度上影响了其稳定性。

本研究使用的ARM9具有低功耗、高性能、高速精准的计算能力和较好的稳定性、相对便宜的价格等特点;同时ARM9相比于DSP处理器,可以运行Linux免费的操作系统,多任务执行,有利于嵌入式系统的升级和更新。利用ARM9的嵌入式系统作为纸币数字水印的检测装置,可以快速识别纸币,且有利于检测装置的升级。

1 数字水印的嵌入

1.1 数字水印技术

数字水印技术将一些标识信息直接嵌入数字载体,而不影响原载体的使用价值,也不容易被人的知觉系统觉察或注意到,只有通过专业的检测器和阅读器才能提取。

经过数十年的研究数字水印技术取得了很大的进步,见诸各种文献的水印算法有很多种,然而从水印嵌入方式的角度来看,图像水印算法主要分为两大类:空间域水印算法和变换域水印算法。空间域算法的特点是直接对原始图像的像素值作修改,比较典型的空域算法包括文本水印算法、Schyndel算法和Patchwork算法等[4]；空间域算法虽然简单但是水印容量小,鲁棒性差,现在已经很少单独用这些方法了。变换域水印算法内嵌水印容量较大,且水印具有不可见性,鲁棒性也较好。目前数字水印嵌入模型大多采用如下两种公式[5]:

F=x+awi

(1)

F=x+aiwi

(2)

式(1)为加法法则,式(2)为乘法法则。式(1)、(2)中,F为添加水印后的变换域系数,x为变换域的系数,awi为加入的水印强度,ai为添加水印的拉伸因子,wi为水印系数。

在嵌入模型的基础上,为了保持水印的不可见性,同时提高水印的鲁棒性,本研究提出小波变换系数的自适应数字水印技术,根据小波系数的不同添加不同强度的数字水印。

1.2 数字水印的置乱

纸币上的号码是银行发行纸币过程中对纸币进行的编号,每张纸币的号码都是唯一的,因此选取纸币号码作为数字水印。通过对比提取数字水印号码与纸币真实号码是否重复,判别纸币真伪。

为了增加水印的破解难度,在数字水印嵌入宿主图像之前进行置乱处理,使水印像素空间的相关性最小。选取的数字水印图像为19×133的纸币号码灰度图像,如图1所示。

图1 数字水印图像

Fig.1 Digital watermark image

采用Arnold变换对数字水印图像置乱,传统的二维图像置乱变换一般用于正方形图像处理,对宽高不等的矩形图像需进行正方形扩展,或使用高维置乱变换阵置乱。只要M/N为整数值,则二维非等长的Arnold变换周期即存在[6],其中M为行,N为列。Arnold变换公式如下:

(3)

设图1为A,在进行Arnold变换时将A转置,然后二值化,其灰度直方图如图2所示。

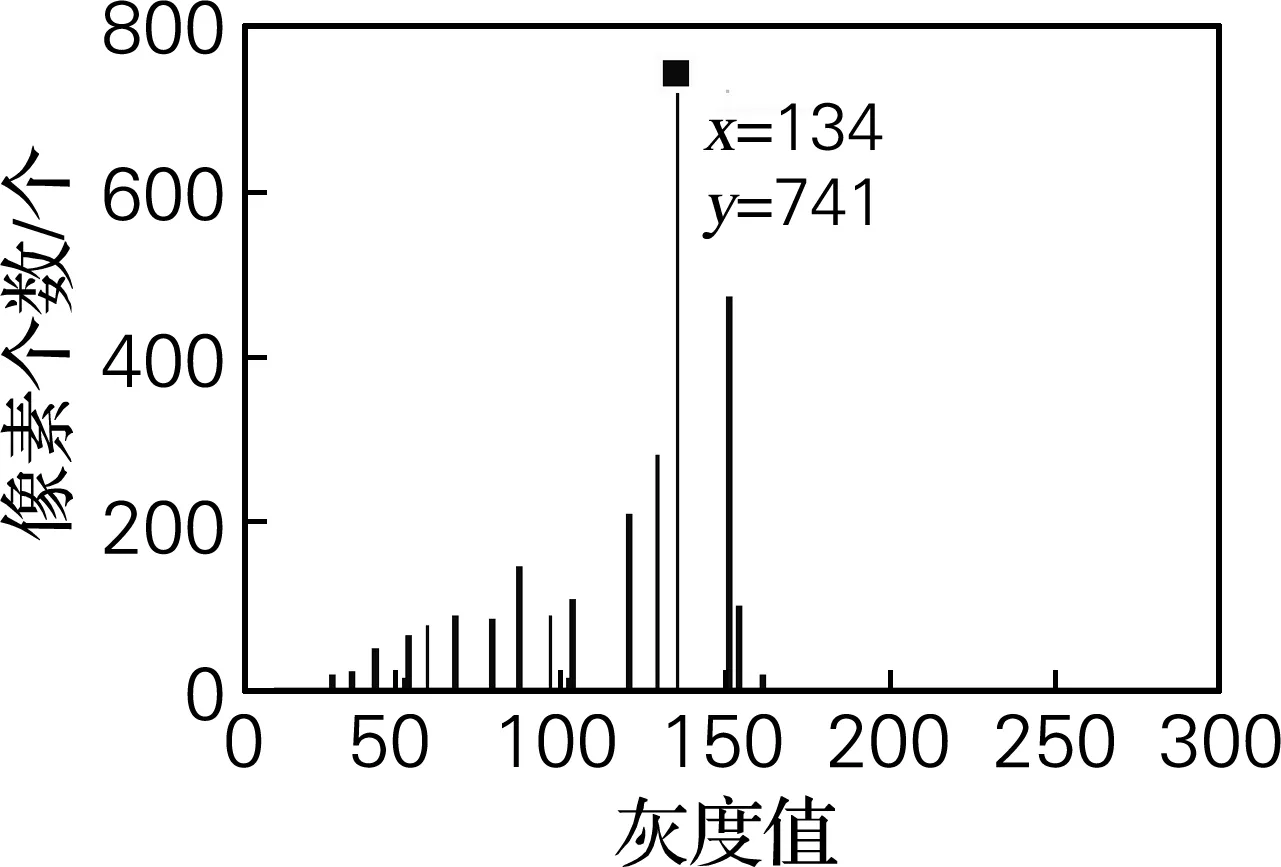
图2 纸币号码灰度直方图

由于直方图是多峰分布,所以可以采用OTSU算法[7]。OTSU算法是以最佳门限将图像灰度直方图分割成两部分,使两部分的类间方差取得最大值。当类间方差为最大时,计算出的像素值即为最佳门限。类间方差与门限值的关系如图3所示,取得最佳门限为108。

图3 门限k与类间方差的关系

A二值化后进行Arnold变换,设参数a=1,b=1,c=1,d=2。经一次变换原来位置(x,y)处的像素值到(x′,y′)处,即

x′=mod (x+y,133)

(4)

y′=mod (x+2y,19)

(5)

这样可能会使坐标x′,y′为0,对于超出位置范围可改为:

x′=mod (x+y,133)+1

(6)

y′=mod (x+2y,19)+1

(7)

通过循环进行Arnold变换,直到x′=1,y′=1,计算得周期T=63。通过计算置乱度选取水印置乱的次数,置乱度用符号ZLD表示,(i,j) 点像素与它相邻的8个像素的平均距离设为D(i,j),边界点除外,则ZLD为:

(8)

计算变换1～62次的ZLD结果如图4所示。

图4 ZLD曲线

图4中,横坐标为变换次数,纵坐标为ZLD,变换次数为23时ZLD最大,所以选取Arnold变换次数为23。变换后的水印如图5所示。

图5 变换后的数字水印

Fig.5 Digital watermarking after transformation

1.3 水印嵌入位置选取

载体图像经过二层小波变换后大部分能量集中在低频域,将水印嵌入低频域提高了鲁棒性,却降低了不可见性,而将水印嵌入高频域中水印又降低了鲁棒性。为此,根据人的视觉特性[8],本研究选取低频域小波系数变化大的地方嵌入适当强度的水印。在低频域嵌入水印提高了鲁棒性,在小波系数变化大的地方嵌入适当的水印增加了水印的不可见性。

设LL1为二层小波低频域,LH1为二层小波域垂直高频分量,HL1为二层小波域水平高频分量,HH1为二层小波域对角线方向的高频分量。测得LH1、HL1、HH1 3个高频分量中LH1的能量最大,在LH1中选取小波系数大的19×133个像素点记录位置,作为水印的嵌入位置。高频域表示的是图像的细节,高频域的小波系数越大表明低频域的小波系数变化越大,所以通过高频域的系数确定在低频域的嵌入位置,在LL1中按在LH1中选的19×133个位置嵌入水印。

1.4 水印嵌入

二值化后的水印经过置乱形成水印W为19×133的矩阵W(i,j)={0,1},(i,j)是水印的像素位置,在选定的19×133个位置上嵌入水印；PS(x,y)为选取的嵌入位置,当PS(x,y)=1时嵌入；adLL1(x,y)表示加入水印后的纸币图像,经过二层小波变换后低频域的小波系数。

当PS(x,y)=1,W(x,y)=1时,令

adLL1(x,y)=LL1(x,y)+a[LL1(x,y),M]

(9)

当PS(x,y)=1,W(x,y)=0时,令

adLL1(x,y)=LL1(x,y)-a[LL1(x,y),M]

(10)

在保持好的鲁棒性的同时增加不可见性,这里根据mod[LL1(x,y),M]的不同选取不同的a值。其中a为嵌入水印的强度,M为参数,取M=120.56,此值是嵌入位置的小波系数最大值和最小值的平均值,a分别为1,0.5,0.3,0.2,0.16,0.1,0.08,0.06,0.05,0.04,结果如表1所示。

嵌入水印后的峰值信噪比PSNR为42.696,归一化相关系数NC为0.996 72,表明图像有很好的不可见性。

表1 a的取值

2 水印的提取

对含水印的图像进行二层小波变换,LLC1表示二层变换的低频域,在LLC1中提取水印；PS为嵌入的位置矩阵；LL为原始图像的低频域。当PS(x,y)=1时,若mod[LLC1(x,y),120.56]>mod[LL(x,y),120.56],则W(i,j)=1；若mod[LLC1(x,y),120.56]≤mod[LL(x,y),120.56],则W(i,j)=0。

将提取的19×133个系数排列成19×133矩阵,然后执行Arnold变换63-23=40次,提取的水印如图6所示。

图6 提取水印图像

Fig.6 Extracted watermark image

测得PSNR为37.55,NC为1。测试结果表明水印图像在无任何攻击的情况下可以无任何失真地提取出水印信号。

3 性能测试

对含水印图像进行攻击来检测鲁棒性,结果如表2所示。加入水印后的图像经过攻击后提取的水印图像如图7所示。

表2 攻击方式及参量值

图7 提取的水印图像

由表2和图7可见,此算法有较好的抗噪声能力,对纸币的污损、剪切、噪声等操作具有较好的鲁棒性。

4 嵌入式系统的数字水印检测

4.1 数字水印检测装置简介

数字水印检测装置嵌入式系统框架如图8所示。以ARM9 S3C2440为微核心处理器,OmniVision OV9650摄像头为图像采集装置,应用程序完成数字水印的提取以及数字水印和纸币号码相关性的对比。

图8 嵌入式系统的框图

具体实现是将摄像头驱动加入到Linux内核,图像处理应用程序加入到文件系统中,当扫描1张纸币时调用1次图像处理应用程序。图像处理软件实现的是将摄像头采集的含水印的纸币图像二次小波变换,在低频域里根据水印提取算法提取水印,然后和标准水印对比确定其相关性。由于数字水印在嵌入纸币时通过Arnold变换进行置乱,置乱次数为数字水印的一个密钥,将数字水印嵌入到纸币中,其中嵌入位置也已固定,则固定的位置为另一个密钥。只有知道这两个密钥才可以正确识别和添加,并且在数字水印中还可以加入其他的密钥来提高纸币的安全性。

4.2 检测装置的性能测试

采集15张含水印的纸币图像,其中5张为嵌入水印的置乱次数不一样的假币,5张为嵌入位置不一样的假币,5张为按规定嵌入,即为真币。用同一个提取算法提取数字水印,提取的数字水印与标准数字水印的归一化相关系数如表3所示,标准的置乱次数是23。

表3 提取水印的归一化相关系数比较

Tab.3 Normalized correlation comparison of digital watermarking of abstracting

置乱次数归一化相关系数位置不同程度/%归一化相关系数标准嵌入归一化相关系数200.456 350.572 10.995 70250.486 5100.430 90.987 00240.500 8150.249 81.000 00280.334 6200.178 40.978 90350.347 0250.143 20.998 43

由表3知当置乱次数不是23时,提取的水印的归一化相关系数小于0.5,当嵌入的位置与标准的嵌入位置不同时,提取的水印的归一化相关系数小于0.6。由表2和3可知,当归一化相关系数设为0.9时,可准确辨别出纸币的真伪。

其中点钞的速度是20张/s左右,即每隔50 ms 点一张钞票。图像的采样速率是30 f/s,摄像头用33 ms采集图像信息,并保存到SDROM。由于ARM9主频为400 MHz,一个时钟周期为0.002 5 μs。ARM9每个CPU时钟周期都可以完成一个Load或Store指令。本研究水印的提取和相关性的对比所用时钟周期为1万个左右,纸币判别在毫秒级完成,所以在点钞的瞬间可以完成纸币的判别。

5 结 论

该数字水印算法不论对剪切还是有污损的纸币都有较强的鲁棒性,都可以提取相关性较高的水印,且图像滤波对水印也不会有较大程度地损害。纸币检测装置可以准确检出纸币,有效地保证了纸币的安全性,同时,ARM9的高速也满足了检测装置对速率的要求。为了提高图像采集的速度可以换用CIS接触式传感器代替摄像头,在嵌入式系统中利用其可以多任务执行的功能添加如号码定位、磁性号检测等功能。

[1] 陶学恒,里红杰,赵昕,等. 基于数字化的纸币防伪技术:中国, 200810246941.8[P]. 2009-06-10.

[2] 陶学恒,芦金石. 新型验钞机的技术原理及可视化设计[J]. 机电产品开发与创新, 2006, 19(5):77-78,83.

[3] 鲍东山. 复合高技术验钞机:中国, 02104493[P]. 2003-10-08.

[4] van SCHYNDEL R G, TIRKE1 A Z, OSBORNE C F. A digital watermark[C]. Austin:IEEE Proceeding on International Conference on Image Processing, IEEE Press, 1994(2):86-90.

[5] 于帅珍,冯丽平. 数字水印的关键技术[J]. 计算机技术与发展, 2010, 20(2):148-151.

[6] 邵利平,覃征. 二维非等长图像置乱变换[J]. 电子学报, 2007, 35(7):1290-1294.

[7] 张华熊,仇佩亮. 置乱技术在数字水印中的应用[J].电路与系统学报, 2001, 6(3):32-36.

[8] MACQ B M, QUISQUATER J J. Cryptology for digital TV broadcasting[J]. Proceedings of the IEEE, 1995, 83(6):944-957.