基于频域分析的图像匹配定位算法的研究

杨喜东

（西南科技大学信息工程学院，四川 绵阳621010）

0 引 言

图像定位匹配比较一直是图像检测中的关键问题，经常用于印刷、影印等行业的产品自动化质量检测系统中。目前的质量检测系统一般将标准模板图像与实际产品的采集图像进行匹配，通过检测比较的结果来确定生产线上的产品是否符合质量要求，但缺点在于定位精度有限，在提高精度的情况下速度又非常低。针对这些缺陷，本文提出了一种基于傅里叶变换和积分图的图像匹配定位算法，旨在解决以往图像定位匹配精度和速度的问题，从而提高工业生产线上自动化检测的效率。

1 算法的提出

1.1 基于频域的抗旋转图像匹配算法

该算法是采用频域匹配的中间结果即图像的功率谱求旋转角。具体图像旋转校正方法如下：

设图像旋转变化角θ范围为［θmin，θmax］，根据旋转校正精度的具体要求，确定θ角改变的步长为△θ，则有θi＝θmin＋i△θ（i＝0，1，2，...，n）。其中：n＝（θmax－θmin）／△θ，则有：

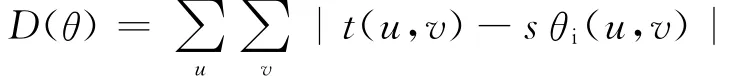
式中，t（u，v）为模板图T（x，y）的功率谱；sθi（u，v）为搜索图S（x，y）的功率谱s（u，v）相对于其中心旋转θ角后得到的新的功率谱，则满足D（φ）＝ min｛D（θ）｝的角即为所求的旋转角。但是此方法无法正确估计旋转角并且信噪比无法达到最大，所以增加带通滤波器，同时对图像作加权、选择候选校正角及图像滤波处理。实际在运用时一般将匹配分成两个步骤：粗匹配和精匹配。其具体流程图分别如图1、图2所示。

1.2 相关函数傅里叶变换的匹配算法

利用二维傅里叶变换进行图像匹配，图像匹配的互相关函数定义如下：

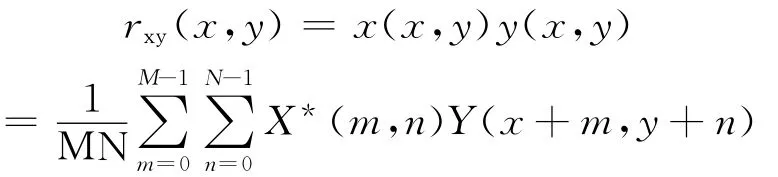
式中，X＊（m，n）表示X（m，n）的复共轭，在图像处理中，函数是实函数。所以X＊（m，n）＝X（m，n），卷积理论同样适用。则傅里叶变换对

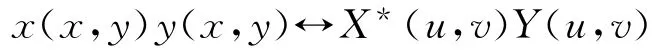
成立。该变换对说明了两个函数的空域相关可以由X＊（u，v）Y（u，v）的傅里叶反变换得到，则频域的相关简化也可以简化为空域的相乘。则

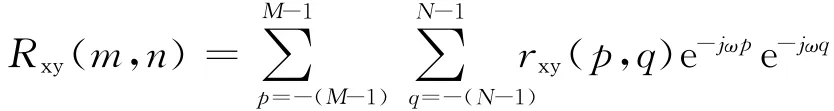
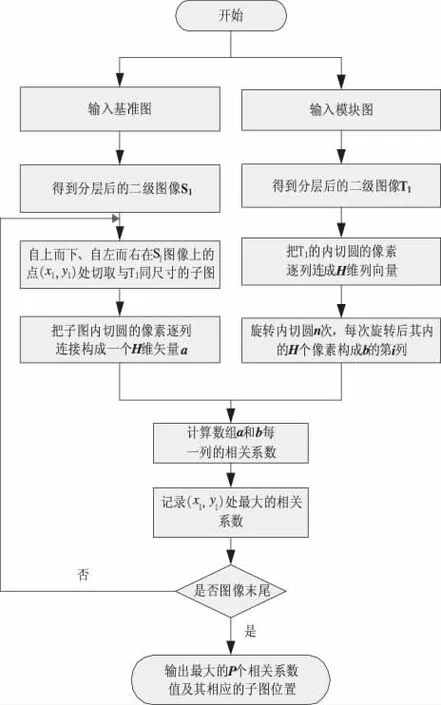
图1 抗旋转粗匹配流程图

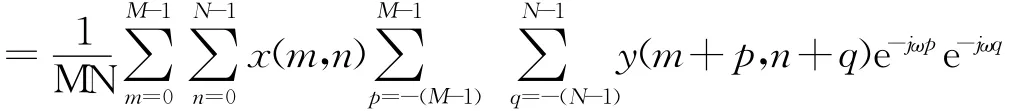
对x补零使其为2 M×2 N矩阵，则上式可以变换为：

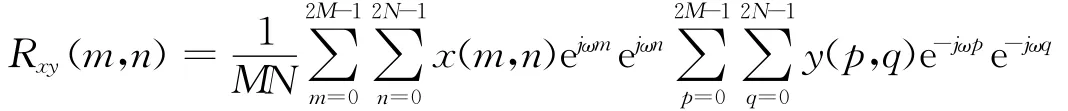
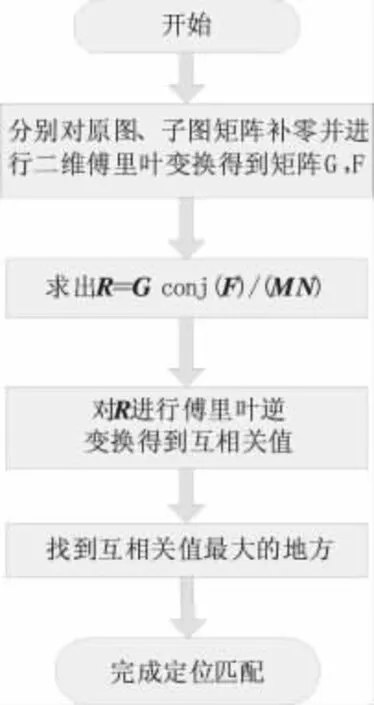
图3 互相关匹配流程图

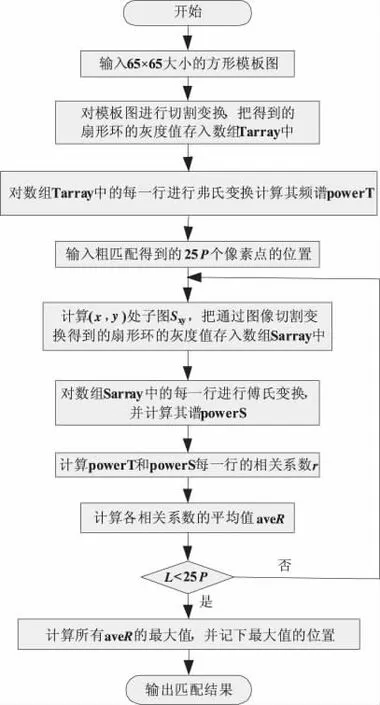
图2 抗旋转精匹配流程图

1.3 MATLAB实验仿真与分析

实验选取的是大小为550×578，格式为b mp格式的一幅图像，然后在该图上截取一幅较小的图片为模板图片。匹配后用红色的方框在待匹配的图像中将模块图标识出来。下面用三种方式进行模板的匹配定位。通过MATLAB编程实现三种常见的图像匹配算法，通过比较，分析各种算法的优缺点如表1所示。

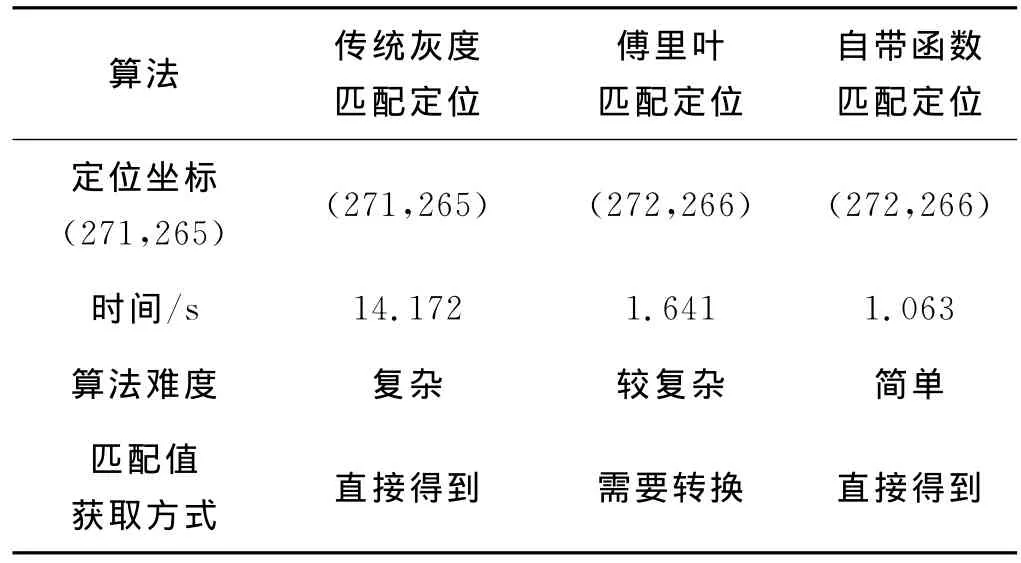
表1 匹配定位比较表

2 算法的优化

针对传统相关匹配计算复杂度大的缺点，基于快速傅里叶变换（FFT）和积分图提出了一种快速相关匹配算法，大大降低了传统相关匹配的计算复杂度。同时，该算法在任意搜索位置提供了与传统相关匹配完全一致的计算结果，天然地继承了传统相关匹配抗干扰能力强、定位准确度高的优点。

2.1 优化过程

设模板图像为T，大小为m×n，基准图像（待搜索大图）为S，大小为M×N，且m≤M，n≤N。设S中以（x，y）为左上角，点大小为m×n的子块为Sxy，通过对相关系数矩阵ρ（x，y）的分析，判断两幅图是否匹配。其中

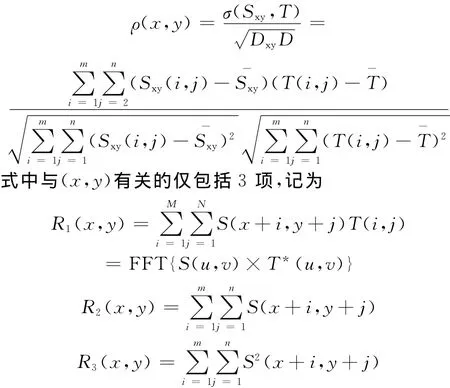
其中R2（x，y）和R3（x，y）分别为子块Sxy灰度值及其能量的积分，本算法利用积分图对其进行快速计算。对任意图像g，其积分图在（x，y）处的灰度值ii（x，y）为图像g中该点左上方所有像素灰度值的积分，即：

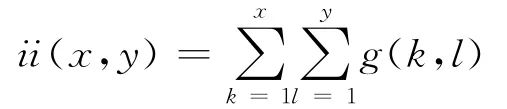
该积分图可以由下面两个公式对原图g一次扫描得到

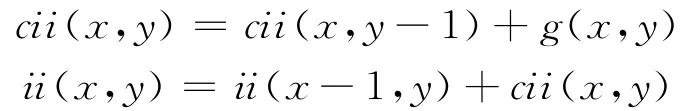
式中，cii（x，y）表示点（x，y）所在列纵坐标不大于y的所有像素灰度值的积分，即

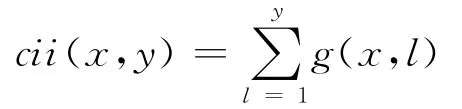
则优化后的快速相关匹配算法流程图如图4所示。

2.2 优化后的特点

（1）计算复杂度降低

传统相关匹配的计算量主要取决于占主导地位的乘法运算次数。对任意搜索位置（x，y），基准图像遍历搜索共需计算（M－m＋1）（N－n＋1）个搜索位置，从而传统相关匹配所需乘法运算次数为

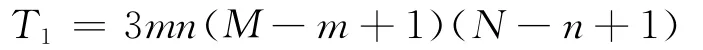
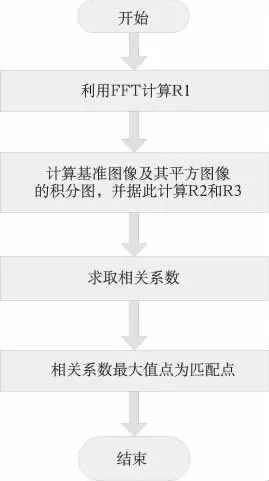
图4 利用积分图匹配算法流程图

其计算量近似与模板图像大小和基准图像大小的乘积成正比，随二者的增大而快速增加。而算法优化后的快速相关匹配算法由于积分图仅涉及有限次的加法运算，因此算法复杂度主要由FFT及IFFT决定。典型的FFT及IFFT所需乘法运算次数均约为2 MN l og2（M／N），R1（x，y）共需计算一次 FFT和一次IFFT，从而其所需乘法运算次数为

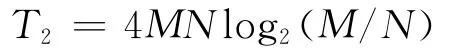
本文算法的计算复杂度与模板图像大小无关，其计算量与传统相关匹配的计算量之比为

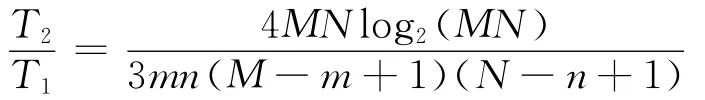
从上式可以看出，随模板图像大小m的增大，本文算法与传统相关匹配计算量之比快速降低，即模板图像和基准图像尺寸越大，本文算法相对传统相关匹配的优势越大。

（2）高精度和抗干扰能力

为了验证优化后算法的有效性，采用MATLAB对优化后算法进行了编程实现，并将结果与前面的传统匹配算法进了对比。图5是直接对待匹配图进行匹配，并在待匹配图中用红色矩形框将定位图像标示出来。

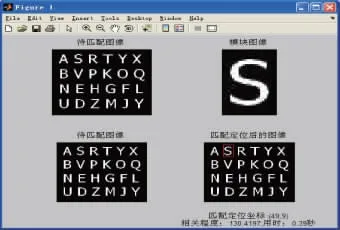
图5 利用积分图匹配定位效果图

从图中可以看出匹配所用的时间在0.39 s左右，而且匹配的精度很高。由此可以得出基于傅里叶变换和积分图的匹配定位算法具有很好效率，并且有很好的抗干扰能力。

3 结 论

如何准确、快速的进行图像匹配是当前许多领域关注的热点。然而由于空域算法的复杂性，很多空域的匹配方法都很难在实际中应用，因此本文阐述的基于频域的图像匹配方法体现出了一定的理论意义和实际价值。同时解决了传统的图像定位匹配中定位精度和速度不能兼顾的缺陷。当然图像匹配是一个复杂和不断完善的过程，在今后的研究中，该算法还有一些值得改善和优化的地方，如扩大算法的适用范围和通用性、提高抗干扰能力、减少图像匹配时间等，但随着社会经济发展的不断进步，图像匹配技术必将拥有更广阔的发展前景。

［1］ 王小睿，吴信才.遥感多图像的自动匹配技术［J］.中国图形图像学报，1997，10（2）：735－738.

［2］ 孙 瑾，顾宏斌，秦小麟.一种鲁棒型 Hausdorff距离图像匹配方法［J］.中国图象图形学报，2008，4：761－767.

［3］ 李晓明，张福继.一种基于学习的自动图像匹配检验方法［J］.自动化学报，2008，1：7－13.

［4］ 邓通军.旋转图像匹配新算法［J］.测绘与空间地理信息，2007，8：104－108.

［5］ 李 卓，邱慧娟.基于相关系数的快速图像匹配研究［J］.北京理工大学学报，2007，（27）11：998－1000.

［6］ VIOLAP，JONESM .Rapid object detection using a boosted cascade of simple features［C］.IEEE Conference on Co mputer Vision and Patter n Recognition，2001，511－518.