近海中不同数量补偿阳极的电场特性研究
卞强 柳懿
(海军工程大学电气与信息工程学院,武汉 430033)
1 引言
舰船是由不同的金属建造而成,这些金属在海水中具有不同的电位,便会在舰船的周围海水中形成电场。此电场对舰船会形成两种影响:(a)此电场会使得舰船船体的金属慢慢腐蚀,影响舰船的使用寿命;(b)此电场会被探测到,成为水中兵器新的信号源,降低了舰船的安全性。现有的减少舰船周围海水中电场的主要方法是通过外加电流到补偿阳极产生的反向电场对原始电场进行抵消。本文对不同数量的补偿阳极对舰船周围海水中电场的影响进行分析[1~3]。
2 数学建模
海水中的点电极场源是最基本最简单的一种电磁场场源,对于小尺寸电极产生的电磁场可以直接用点电极描述[5]。补偿阳极的外形近似三个大约120°的弧形组成的环形,每个弧形电流源在海水中形成的电场可以近似等效为点电极形成的电场。对分割后各小段电流形成的电场进行矢量叠加就能近似得到补偿阳极的电场分布[6]。
海水是一种导电介质,对于浅海则应等效为空气—海水—海床三层介质平行界面模型。根据静态电磁场的拉普拉斯方程及其电位的约束方程,基于实际应用的考虑,求解拉普拉斯方程就可以得到空气—海水—海床三层模型中点电极场源产生的电场强度。三层模型中点电极产生的电场强度表达式的导出为舰船补偿阳极建模与计算奠定了理论基础[7]。
下面对单个环形电流源建立模型。设单个环形电流源的电流为I且均匀分布,将环形电流源分割成n(n为常数,且足够大以确保计算精度)个小段的弧形电流源,则每个小段的弧度为2/nπ。第k(k为常数且1kn≤≤)个小段的中心弧度为2kπ/n,电流为I/n。因为分割次数较多,所以单个小段的弧形电流源尺寸较小,可以直接用点电极描述。选取直角坐标系O-XYZ,原点O位于距离该环形电流源圆心垂直上方d处。以坐标面z=0和z=h为边界面,z<0为场区0,0<z<h为场区1,z>h为场区2,场区0、场区1和场区2分别为空气、海水和海床。假设空气、海水和海床均为线性、均匀和各向同性媒质,场区0空气空间的电磁参数分别为介电常数ε0、磁导率μ0和电导率σ0,场区1的电磁参数分别为介电常数ε1、磁导率μ1和电导率σ1,场区2的电磁参数分别为介电常数ε2、磁导率μ2和电导率σ2。此船体补偿阳极位于0<z<h的海水区域,且圆心坐标为(0,0,d)(0<d<h),电流输出方向沿Z轴正方向[8]。
通过上面的计算得到了任意一个小段弧形电流源在海水中产生的电场强度表达式,将环形电流源分割后的n个弧形电流源产生的电场强度矢量相加,即可求得单个补偿阳极的电场强度三个分量表达式如下:
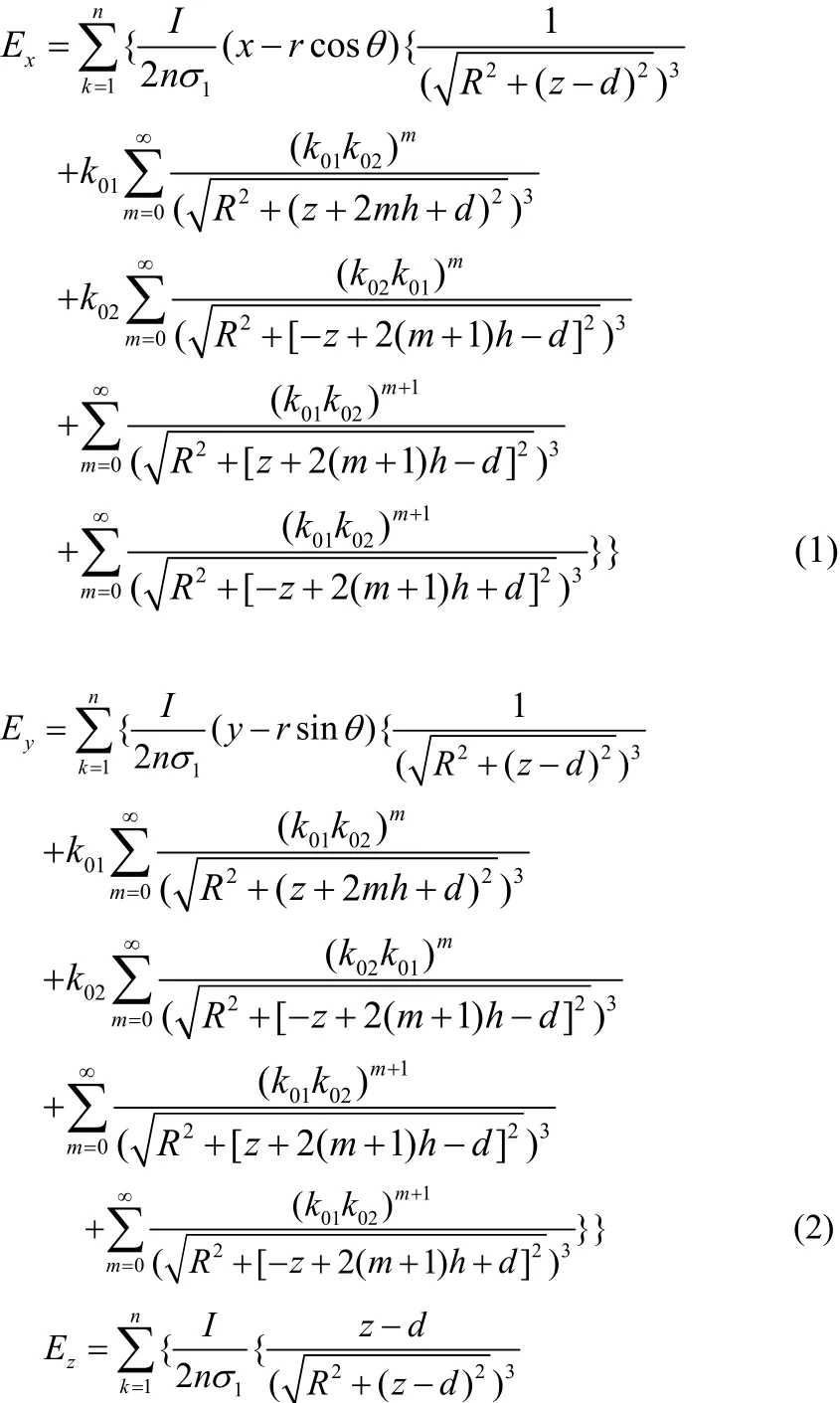
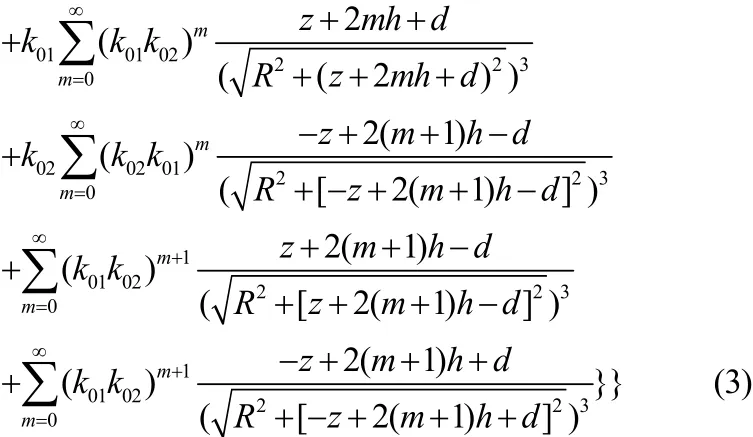
3 不同数量补偿阳极电场分布特性分析与比较
3.1 单个补偿阳极电场分布特性分析
建立单个补偿阳极在海水中产生的电场强度计算模型:补偿阳极与海水平面平行,设海水平面为XY平面,Z轴正方向为垂直海水平面向下,环形阳极半径为12.5 cm,电流大小为10 A,海水电导率为4 S/m,当补偿阳极圆心位置分别为(0,0,2)时,在海水中8 m深处的平面上产生的电场强度三分量分布如图1所示[8,9]。
单个补偿阳极电场分布特性分析:
(1)电场Ex分量在四个象限的极性变化为:在第一、第四象限为正值,而在第二、第三象限是负值。在补偿阳极圆心的正下方为零,即电场的死区,也是两种极性的分界点。并在X轴上产生的电场强度最大,在补偿阳极与X轴正方向和负方向相交的正下方处为正峰值和负峰值,也是绝对值最大的地方,随着与补偿阳极圆心距离的正向和负向增大,电场强度逐渐减小和增大。
(2)电场Ey分量在四个象限的极性变化为:在第一、第二象限为正值,而在第三、第四象限是负值。在补偿阳极圆心的正下方为零,即电场的死区,也是两种极性的分界点。并在Y轴上产生的电场强度最大,在补偿阳极与Y轴正方向和负方向相交的正下方处为正峰值和负峰值,也是绝对值最大的地方,随着与补偿阳极圆心距离的正向和负向增大,电场强度逐渐减小和增大。
(3)电场Ez分量在四个象限的极性变化为:在四个象限均为正值。在补偿阳极圆心的正下方为正峰值,也是绝对值最大的地方,随着与补偿阳极圆心距离的正向和负向增大,电场强度逐渐减小。并且Ez分量的正峰值大约是Ex和Ey分量峰值绝对值三倍大小。
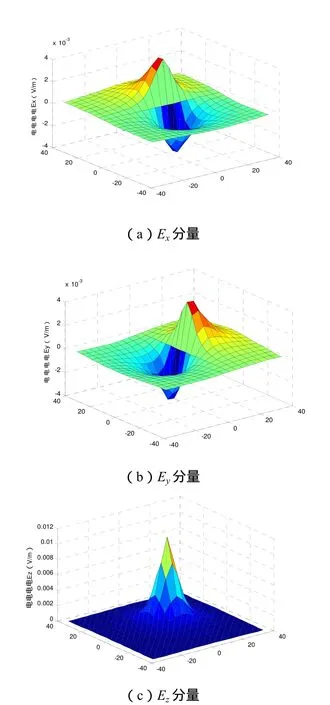
图1 单个补偿阳极电场强度分布
3.2 双补偿阳极电场分布特性分析
在同一坐标系下,将两个补偿阳极进行叠加即可得到双补偿阳极在其周围海水中的电场强度分布。建立两个对称补偿阳极在海水中产生的电场强度计算模型:两个补偿阳极均与海水平面平行,设海水平面为XY平面,Z轴正方向为垂直海水平面向下,环形阳极半径均为 12.5 cm,电流大小均为10 A,海水电导率为4 S/m,当两个补偿阳极圆心位置分别为(-3,0,2)和(3,0,2)时,在海水中8 m深处的平面上度三分量分布如图2所示。
双补偿阳极电场分布特性分析:
(1)电场Ex分量在四个象限的极性变化为:在第一、第四象限为正值,而在第二、第三象限是负值。在两个补偿阳极中心点的正下方为零,也是两种极性的分界点。并在X轴(两阳极的垂直中心线处)上产生的电场强度最大,在第一、第四象限和第二、第三象限的垂直中心线正下方处出现正峰值和负峰值,也是绝对值最大的地方,随着与补偿阳极圆心距离的正向和负向增大,电场强度逐渐减小和增大。
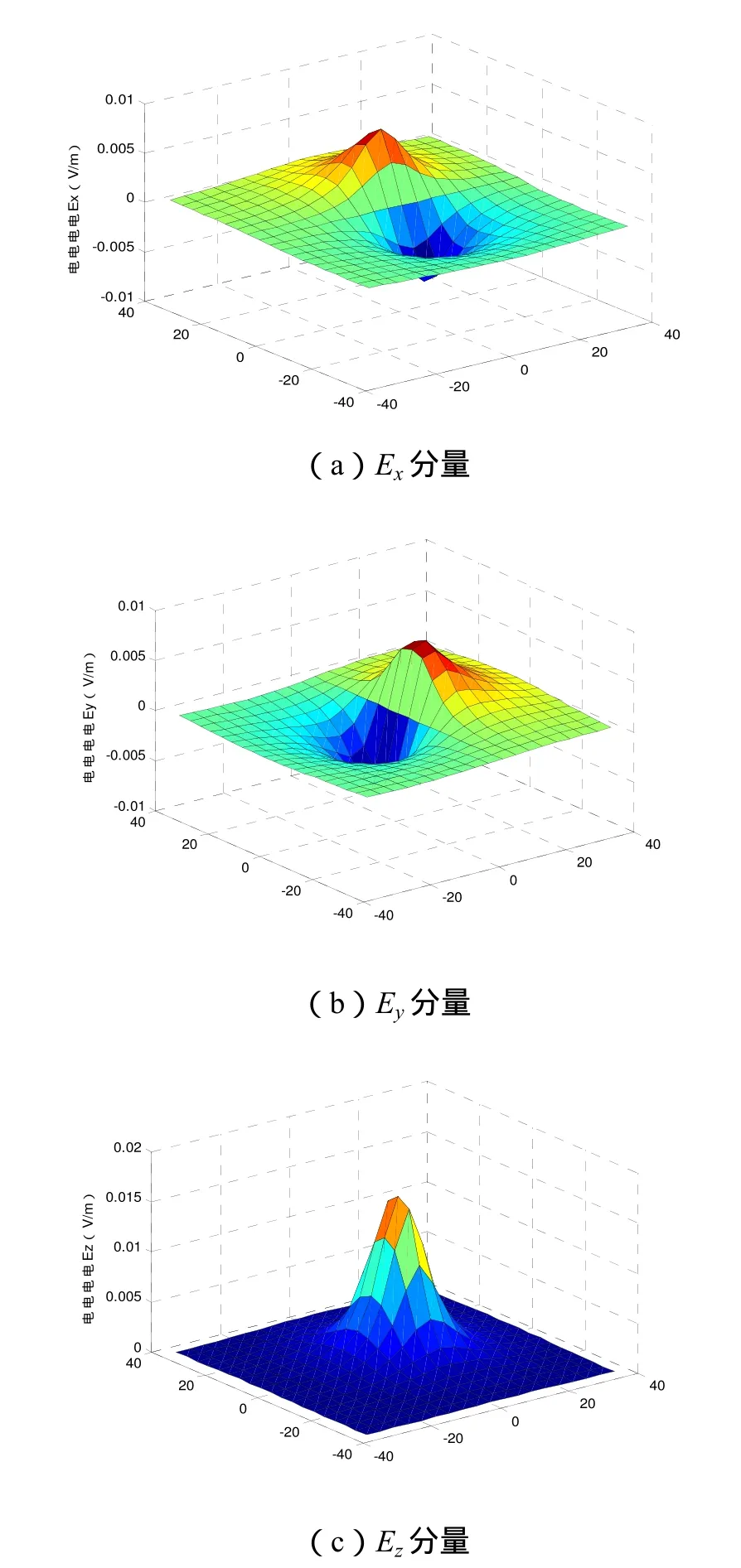
图2 双补偿阳极电场强度分布
(2)电场Ey分量在四个象限的极性变化为:在第一、第二象限为正值,而在第三、第四象限是负值。在两个补偿阳极中心点的正下方为零,也是两种极性的分界点。并在Y轴(两阳极的中心线处)上产生的电场强度最大,在第一、第二象限和第三、第四象限的中心线正下方处出现正峰值和负峰值,也是绝对值最大的地方,随着与补偿阳极圆心距离的正向和负向增大,电场强度逐渐减小和增大。
(3)电场Ez分量在四个象限的极性变化为:在四个象限均为正值。在两个补偿阳极中心点的正下方为正峰值,也是绝对值最大的地方,随着与两个补偿阳极中心点距离的正向和负向增大,电场强度逐渐减小。并且Ez分量的正峰值大约是Ex和Ey分量峰值绝对值四倍大小。
4 实验验证
在某海域使用水下电场测量装置对被测船体的水下电场进行实地测量,测量点的总体分布情况如图3所示,其中B为船宽。舰船采用双阳极补偿方式。
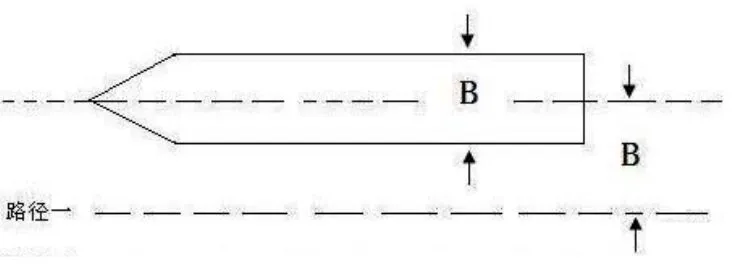
图3 舰船电场测量点分布图
理论上测量平面应该为无限大平面,但实际测量中由于条件所限,本次测量只是在距离船的中轴线一倍船宽的地方进行测量。方向为从船首至船尾,实验中用一艘小船拖拽着水下电场测量装置匀速通过,得到相应的数据。
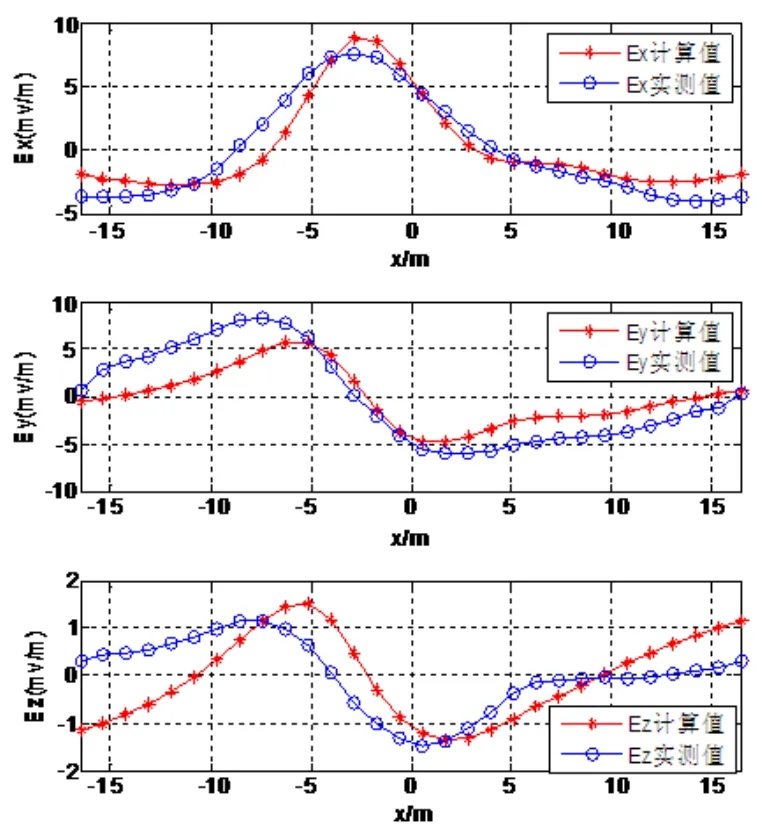
图4 舰船电场实测值和计算值的对比
由图4可得,电场的实际测量值与通过模型换算得到的计算值还是非常吻合。本文所进行的仿真结果可以很好的反映实际舰船的情况。
5 结束语
本文通过分析单个补偿阳极、双补偿阳极的电场分布,可以清楚的得到以下结论:1)对比两种情况的Ex、Ex和Ez三个分量的电场分布图,可发现补偿阳极数目越多,各个分量电场中的峰值处的图形就越平缓。2)对于各分量电场,补偿阳极越多,Ez分量的电场峰值下降的越多。
[1]郑军林, 陈新刚, 郑春军, 赵留平. 舰船电场隐身技术.中国舰船研究, 2006: 48~51.
[2]卢新城, 龚沈光, 刘胜道, 孙明. 舰船极低频电场的产生机理及其防护. 海军工程大学学报, 2003: 70~74
[3]喻浩. 舰船电场和低频电磁场防护措施[J]. 舰船科学技术, 2000(3): 37~39.
[4]HUBBARD J C, BROOKS S H, TORRANCE B C Practical measures for reduction and management of the electromagnetic signatures of in-service surface ships and submarines UDT, [C]. 1996: 64~65.
[5]DYMARKOWSKI K, UCZCIWEK J. The extremely low frequency electromagnetic signature of the electric field of the ship UDT[C].2001: 1~6.
[6]HARRISO.A.S, HUBBARD.J.C, An underwater electric potential (static electric) signature management toolkit for the non-specialist Conf proc, UDT, Europe[C]. 1994:477~481.
[7]杨振, 王向军, 张民. 舰船电场防护中补偿阳极电流数值仿真研究. 系统仿真学报, 2009: 6029~6032.
[8]SCHWEFELH. P. Numerical optimization of computer models [M].Chiches-ter: Wiley, 1981.
[9]YAO X, LIU Y.A new evolutionary system for evolving artificial neural networks [J]. IEEE Transactions on Neural Networks,1997, 8(3):694-713.

