PD雷达解速度模糊中冗余量的选择分析
孙义 王雅
(1. 驻武汉地区军事代表局,武汉430064; 2. 武汉船用电力推进装置研究所,武汉 430064)
0 引言
模糊问题是PD(pulse Doppler,脉冲多普勒)雷达的固有问题。尤其对于中重复频率(Medium-PRF)雷达体制,存在距离和速度上的双重模糊[1-4,6]。因此在 PD雷达中,常常要求进行解模糊处理。对于距离模糊,由于目标距离单元或者距离门的误差范围比较小(一般在2±以内),解模糊时冗余量设定相对确定,采用搜索法或查表法便可提取目标的真实距离[3]。但对于速度模糊,由于其速度信息仅由覆盖对应PRF的一组邻接的窄带滤波器组滤波得到[2,6],当滤波器的数目有限时,其多普勒信息在频域上通常都近似为窄带滤波器组中输出功率最大的通道对应的中心频率,即速度取值的离散化[6]。而当目标的真实多普勒频率位于两多普勒通道之间时,通过上述估计得到的结果将不能反映其真实信息,从而造成很大的测频误差。特别地,对于多组PRF,滤波器的数目确定时,不同PRF的频率估计误差多不相同。这将会对冗余量的确定造成很大的影响。本文首先分析解速度模糊的实现及存在的问题,简要对比相控阵雷达利用数字波束形成(DBF)搜索方位与 PD雷达测频的相似性,提出一种降低冗余量的方法,使用该方法能提高各PRF得到的多普勒频率的准确性,避免因近似估计导致的大的测量误差。
1 解速度模糊处理中的问题
PD雷达常规解模糊处理是以窄带滤波器最大输出的中心频率或其归一化为依据的[6]。如下图(1)为某 PRF下的窄带滤波器组频率响应。设脉冲重复频率为rf,该PRF下窄带滤波器数目为 N,则频率分辨力为 Δ=f/N。对于一个r具有速度 V =λfd/2(fd=fd' +nfr,fd'为模糊频率,n为模糊数,λ为载波波长)的目标,经滤波器组滤波后可得到如图(2)所示的输出结果,其中输出幅值(功率)最大的通道号对应的中心频率认为是fd'的近似估计。
解模糊方法就是利用多组 PRF滤波后的估计频率或归一化频率进行解模糊。文献[1]和文献[2]给出了用搜索法和查表法进行解速度模糊的实现。两种方法都要以一定的冗余量为解模糊准则的,即若对n组PRF下模糊频率的某种变换满足
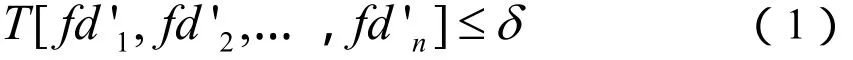
则认为解模糊成功。式中 []T·表示对各PRF下对模糊频率 'fd的变换。在查表法中对应各视在模糊频率单元余数与事先建立余差表之间的绝对差。δ为事先确定的冗余量。当各PRF得到某一目标的模糊频率后,δ的确定将直接影响解速度模糊的准确性。
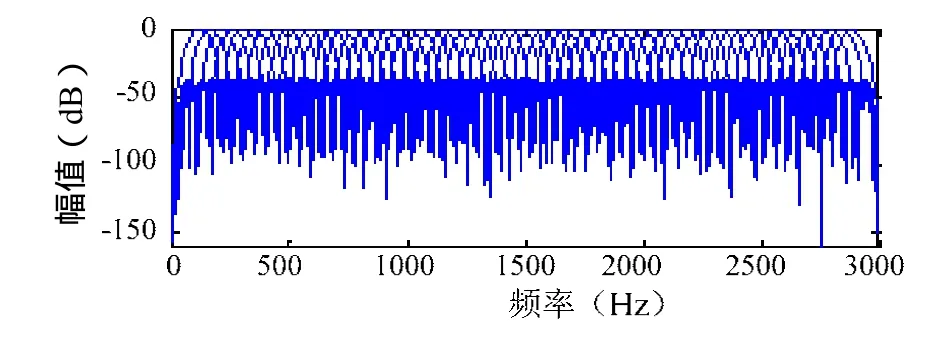
图1 某重频下的滤波器组频率响应

图1 具有多普勒速度的目标滤波后的输出结果
通常对多组PRF,用对应滤波器组对脉冲串进行滤波后,可以得到各PRF下的模糊频率 'fd。同时PRF的不同会导致对同一目标速度V, 'fd和n的取值不同。并且因为频率分辨力的影响,模糊频率偏离目标真实多普勒频率的误差也就无法精确判断。表1列举了某四重PRF组合下,当滤波器数目N=60时的最大频偏误差列表。
滤波器组在实际工作时总要受到噪声和干扰的影响,因此当某一目标多普勒频率落入滤波器组的通道之间时,滤波后最大输出值可能为邻接通道中的任意一个。在该情况下解模糊时多普勒频率的均方差将非常大。此时用查表法或搜索法解速度模糊,其冗余量的确定便成为解模糊是否成功的最主要问题。大的冗余量将增大解速度模糊的错解率,而采用小的冗余量则又可能漏掉那些正确的速度信息。为确定一个合理的解模糊冗余量,本文在解速度模糊的算法基础上,通过细化估计来降低各PRF的频偏误差,从而降低冗余量大小,提高解速度模糊的准确性。

表1 某重频组合下最大频偏误差与各重频的关系(N=60)
2 降低冗余量的方法分析
冗余量δ的确定主要取决于各 PRF的最大频偏误差,因为降低各PRF的最大频偏误差能有效地降低 []T·的运算结果。另外,在处理过程中也希望各PRF能统一为期望的频率分辨力。考虑到滤波器数目N一定时,各重频频率分辨力是不同的,因此我们需要采用其他方法,将各PRF频率分辨力进行统一。
基于上述的想法,本文对比相控阵雷达中DBF搜索方位和PD雷达频率估计的相似性,将DBF搜索法的思想用于降低频偏误差,从而减小冗余量。相控阵雷达DBF搜索方位主要通过改变DBF权系数实现对空域的方位搜索[6,7],其原理如图3所示。其中(a)为波束扫描图,一般相控阵雷达会把空域分成若干波位,当雷达在某一波位内检测到目标时,虽可确定目标的大体方向,但不能得知其具体方位信息。因此需要在该波束宽度内以满足要求的角度分辨率θΔ进行细化搜索,如图3(b)所示。取该波束内的最大输出对应的方位作为目标角度的估计。
将上述空域搜索思想变换到频域。其共同点有:1)空域方位搜索等效于频域上窄带滤波器中心频率的偏移。2)目标在某一波位检测到峰值等效于频域滤波器组中输出幅值最大的相邻滤波器通道。3)角度分辨力θΔ对应频域中期望的频率分辨力dfΔ。现分析,对目标回波进行整个频域滤波得到输出幅值最大的两个多普勒通道,等效于DBF方位搜索中确定目标所在波位。为满足要求的测频精度dfΔ,可将已知的频率范围再用若干各窄带滤波器覆盖,其中心频率间隔设为期望频率分辨力dfΔ,用这些窄带滤波器对目标回波进行细化搜索,从而降低常规频率估计造成的大的误差。
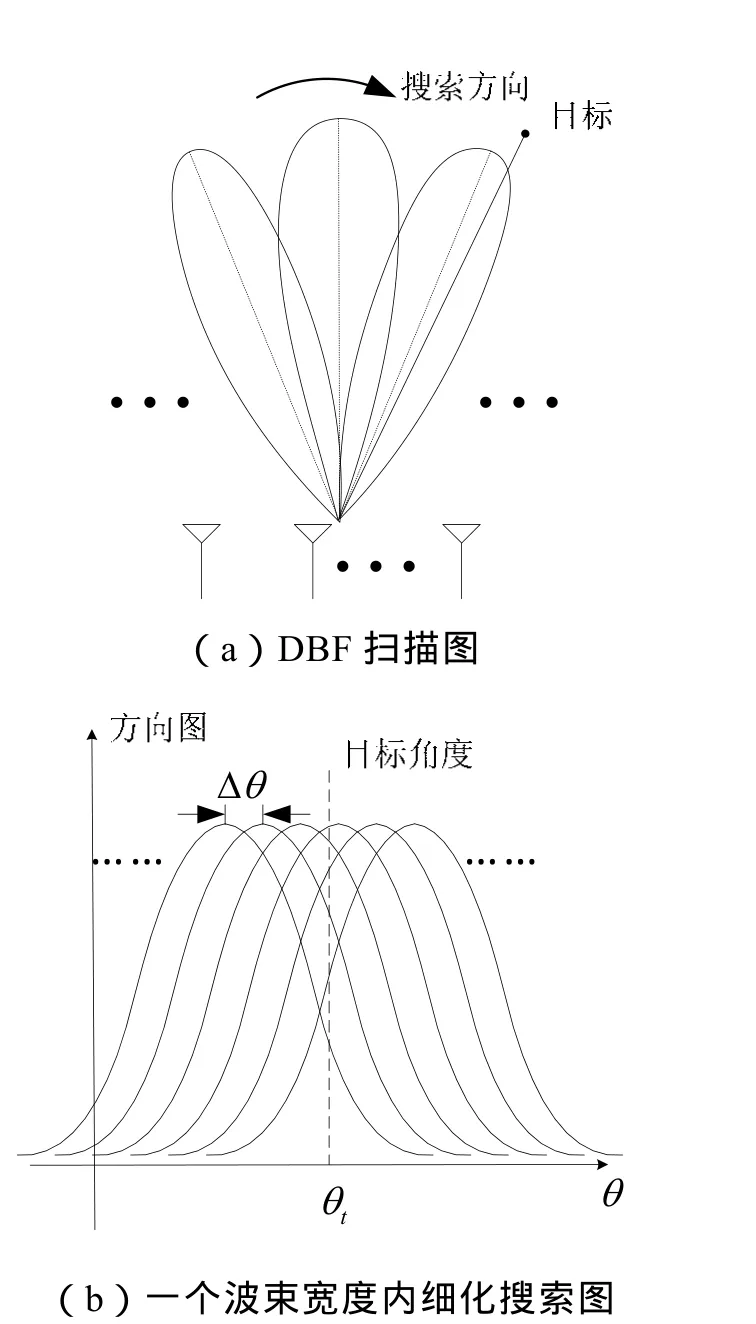
图3 . DBF扫描图和波束宽度内的细化搜索示意图
设脉冲重复频率为fr,有N个窄带滤波器对其覆盖,滤波器的权系数分别为Wi,i=1,2,,…,N。则其频率分辨力为=f/N >Δf。对于输出rd最大的两个多普勒通道,设其通道号分别为i和i+ 1 ,对应中心频率为fi和,取M个窄带滤波器对其频率范围进行二次覆盖,其中M满足M = ( fi+1-)/Δfd。对应滤波器的权系数设为Wij,j= 1 ,2,…,M。则最大信号法测频的处理步骤为:
Step1:对原始数据进行多通道滤波处理,实现对整个频率的搜索,得到输出功率(幅值)
最大的两个多普勒通道。即
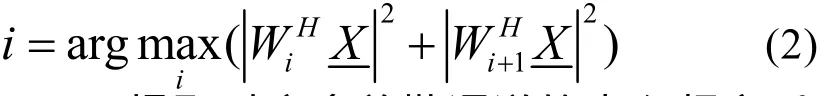
Step2:提取对应多普勒通道的中心频率fi和fi+1,并根据Δfd设计M个窄带滤波器,其权系数分别为Wij,其中心频率分别为fij=fi+j× Δfd。用设计的权系数对数据进行二次处理,得到输出最大功率对应的j,即
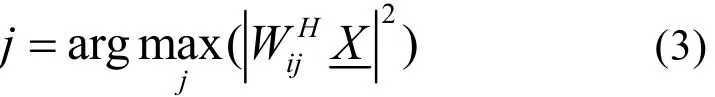
Step3: 利用 fij=fi+j× Δfd得到目标的估计频率。
通过对各 PRF得到的目标回波做上述细化处理,不仅可以更精确地提取目标的多普勒信息,而且通过对M的选择能将各PRF的频率分辨力统一为解模糊处理期望的频率分辨力Δfd。这样,再利用各PRF下的模糊频率fd'来确定解模糊时的冗余量δ就变得相对容易,而且增加解模糊的可靠性。
3 计算机仿真实验
为验证上述算法的正确性,现采用解模糊最小方差作为验证依据。以表1中的四重PRF对应滤波器组对目标回波进行模糊处理,设期望的多普勒频率分辨力为10 Hz。不失一般性,假设目标的多普勒频率为7000 Hz,则经过频率模糊后得到的各PRF滤波器组输出如图4所示。
通常解模糊处理只将输出幅值(功率)最大通道对应的中心频率作为目标模糊多普勒频率的近似估计。通过上图输出结果便可得到常规解模糊处理需要的模糊频率,对应下表。
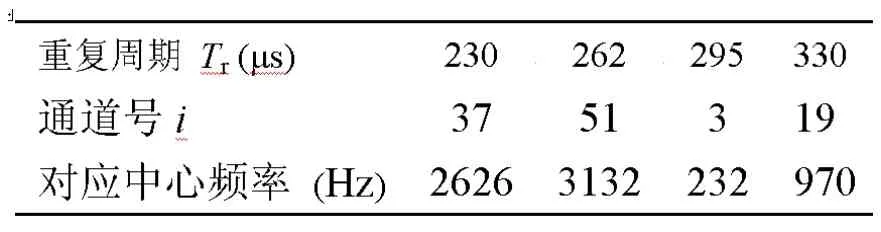
表2 目标在各PRF下的模糊频率对比表
当用文献[1]中给出的搜索算法时,需要求得所有可能值的最小均方误差σ。通过上述数据,我们得到解速度模糊时所有可能值的最小方差为σ= 3 6.58 Hz 。若想正确解速度模糊,则冗余量的选择应大于对应的最小均方误差,即δ>σ。通常对于固定的PRF组合,取其可能频率在该组合下得到的最大均方误差作为δ。而从上述估计中得到的均方误差往往很大,这样就会增大解模糊的错解率。采用文献[2]中所示的方法,也会出现难以判断冗余量δ的值的情况。
在相同的PRF组合下,采用细化搜索方法,即用已知频率范围的若干个窄带滤波器对目标回波再次滤波,把输出最大幅值(功率)的滤波器对应的中心频率作为该PRF的模糊频率。对应图4中最大输出通道附近的滤波结果,如图5所示。
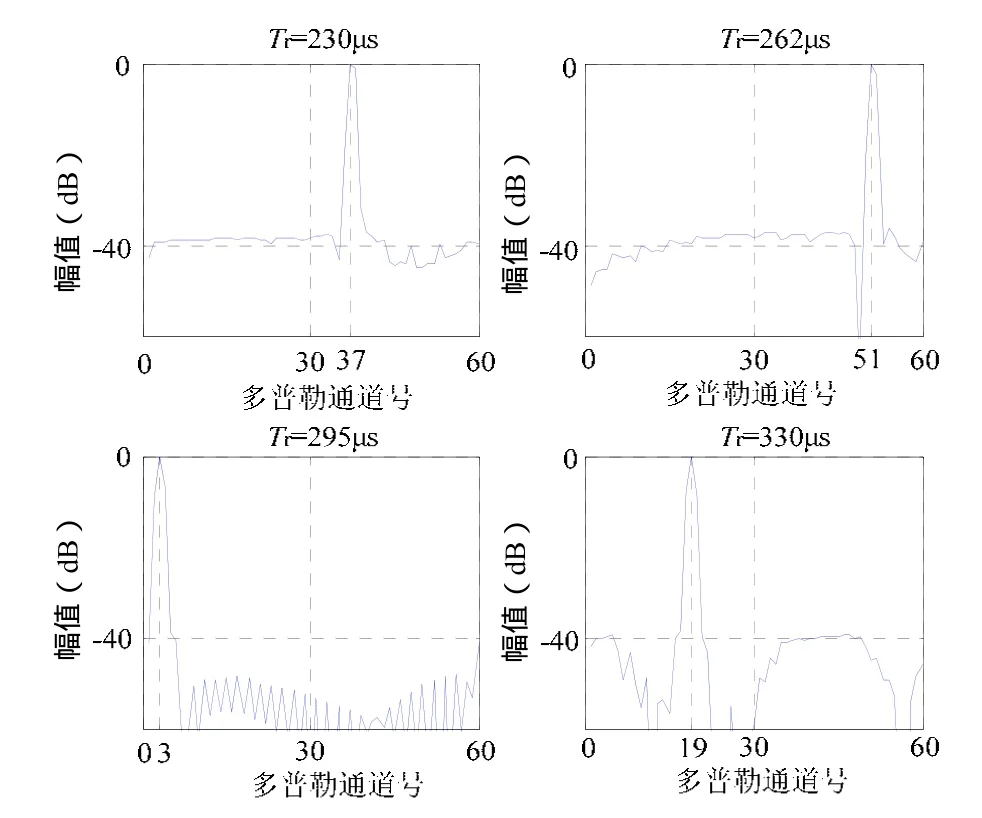
图4 对回波数据进行滤波后的结果

图5 对输出最大的两通道进行二次滤波结果
经过进一步处理后,我们在表2的基础上得到表3的结果。
当采用文献[1]中搜索法解模糊时,其可能值对应的最小均方误差变为 σ = 1 5.22 Hz 。和表2中的结果对比可知,通过细化搜索,各PRF的估计频率值都得到了一定程度的修正,使其解模糊后更接近于真实的目标多普勒频率。这样就可以适当降低冗余量δ的范围,以保证解速度模糊的正确性。

表3 对目标回波进一步处理得到的模糊频率与PRF的关系
5 结论
本文首先分析了解速度模糊中存在的冗余量选取大小的问题,在此基础上对比了相控阵雷达DBF方位搜索方法和 PD雷达频率估计的相似性,并将该思想用于降低解速度模糊时冗余量的选择上。通过大量的数据仿真,说明了该方法能有效修正解速度模糊处理中的估计频率,降低解速度模糊中冗余量的大小,从而保证了解速度模糊的可靠性。
[1]G Trunk, S Brocket. Range and velocity ambiguity resolution[C]. The Record of 1993 IEEE International Radar Conference 1993: 146-149.
[2]雷文, 龙腾, 高梅国等. 脉冲多普勒雷达频域跳盲与频域解模糊[J]. 系统工程与电子技术, 2000,22(8): 95~97.
[3]张代忠, 洪一, 邱炜. 脉冲多普勒雷达中的解模糊算法及实现.[J].雷达科学与技术. 2004:293-297
[4]曾涛, 龙腾. 一种脉冲多普勒雷达解模糊新算法[J].电子学报. 2000,(12): 99~101.
[5]丁鹭飞, 耿富录. 雷达原理[M]. 西安:西安电子科技大学出版社, 2002: 205~209.
[6]毛士艺, 张瑞生, 许伟武等. 脉冲多普勒雷达[M].北京: 国防工业出版社, 1990: 100~200.
[7]张明友. 数字阵列雷达和软件化雷达[M]. 北京: 电子工业出版社, 2008:323~361.

