电磁斥力机构设计方法
姜楠 任志刚
(武汉船用电力推进装置研究所,武汉 430064)
0 引言
早在 1972年,S.Basu就在公开文献中提出基于涡流原理的电磁斥力机构[1],其原理示意图如图1所示,储能电容对励磁线圈脉冲放电,与励磁线圈临近的金属盘感应出与励磁电流方向相反的涡流,从而产生电磁斥力。

图1 电磁斥力机构的基本原理图
该机构的突出优点是动作速度极快,触动时间在百微秒级,传统的弹簧机构、液压机构等都是毫秒级,但是行程较短,通常只有十几毫米。由于当时短路电流水平较低,常规的断路器足以开断。因此没有得到重视与发展。
近年来,随着对触头分断速度有极高要求的中压混合直流断路器以及真空灭弧室的发展,电磁斥力机构得到了国内外学者越来越多的研究。日本三菱电气的学者和山东大学的李庆明等人分别将斥力盘等效为一匝线圈和多匝线圈,推导出了计算电磁斥力机构出力特性与运动特性的解析方法。华中科技大学的王子健对影响斥力机构出力特性的因素进行了研究[2-4]。
前人的工作基本上都是在已知机构尺寸等参数的情况下进行的,属于电磁场的正求问题。而实际工作中,一般都是由对机构特性的部分要求来求解出机构的尺寸等参数,属于电磁场的反求问题。由于斥力机构的物理过程是一个涡流场与运动耦合的复杂过程,影响斥力机构特性的因素很多,因此,斥力机构的反求过程是非常困难的,本文在总结前人的工作基础上,针对一类形式的斥力机构,提出了一种反求的方法。
1 斥力机构的反求方法
电磁斥力机构结构形式多样,外电路形式也变化多端,本文主要针对较常用的一种形式来进行分析计算,推导出斥力机构的反求方法。
1.1 基本假设
假设斥力盘与线圈均为扁圆盘形式,内外径相等,其结构形式如图2所示。外电路采用单一电容放电,外加一续流二极管,其拓扑机构如图3所示,图中TVS为真空触发间隙。

图2 斥力盘与线圈结构形式
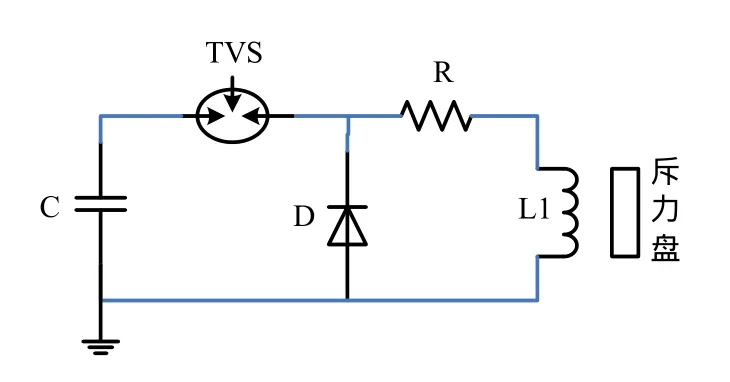
图3 外电路拓扑结构
2.1 快速开关对快速机构的技术要求
快速开关对机构的技术要求有很多,如刚分速度、刚合速度、行程、分闸时间、合闸时间、运动部件质量、分闸保持力、合闸保持力等等。不同的应用场合,所关注的要求有所不同,本文所提快速开关主要用于中压混合直流开断中真空灭弧室的分闸。
这种场合的快速开关主要采用真空快速开关,其对快速机构的要求及本文所采用的参数主要如下:
➢ 运动部件质量m=5 kg;
➢ 行程s=10 mm;
➢ 前3 mm行程时间t3=1 ms;
➢ 分闸时间top=2.8 ms;
➢ 系统电压U=5000 V。
由以上技术要求反求机构尺寸等参数。
需要求解得到的参数有:
➢ 储能电容量C;充电电压U0;
➢ 线圈内半径R1;
➢ 线圈外半径R2;
➢ 线圈高度h1;
➢ 线圈匝数N;
➢ 斥力盘厚度h2;
➢ 斥力盘与线圈初始间隙x。
线圈与斥力盘的初始间隙x越小越好,受绝缘因素影响,一般为 3 mm。斥力盘的外径与线圈外径相等,这样效率最高。斥力盘厚度越大,则运动部件质量越大;厚度过小,会增大电阻而减小感应涡流,一般选择2倍趋肤深度即可。
上述应用场合希望开关的刚分速度越高越好,即参数前3 mm行程时间t3越小越好,对于储能电容来说,电容量越小、充电电压越高,则放电电流上升越快,斥力上升越快,因此,电容电压U0选择为系统电压5000 V,如此也可以减少充电设备。
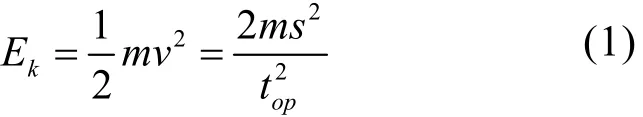
假设斥力盘按匀加速运动,由行程s和分闸时间top求出运动部件最终动能EK:斥力机构将储能电容的能量转化为运动部件的动能的效率η一般为10%到20%,相对较大的电流上升率与较大的运动质量配合以及相对较小的电流上升率与较小的运动质量的配合都会导致电能到动能转换效率较小[5]。此处由于刚分速度较大,要求电流上升率较高,而运动质量较大,因此,效率较低,初步选η=10%。根据能量守恒定律,有如下方程:

由方程(1)和(2)求出电容量C=100 μF。
储能电容参数确定完毕,接下来求解励磁线圈的结构尺寸。
励磁线圈中电流波形如图4所示,分为上升阶段trise和续流阶段tfollow,根据对快速机构的要求的不同,其对应的时间不同。要求刚分速度大的则trise相对要小,斥力上升较快。tfollow大小则是由续流回路的电感电阻决定。
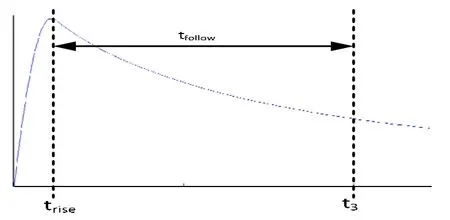
图4 励磁线圈中电流波形
此处取3 mm行程时间t3为上升时间trise的8倍,有方程(3):
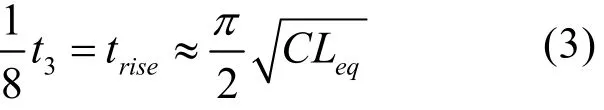
求出等效电感Leq=63 μH。
将斥力盘等效为一匝线圈,励磁线圈与等效线圈的耦合系数为k,励磁线圈电感为L1,有:
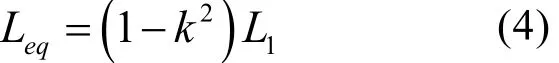
显然,耦合系数k值越大,则斥力盘感应涡流越大,斥力机构出力越大。因此,设计的时候应尽可能地使k值大点。耦合系数k与线圈的外半径高度比成正比例关系,当外半径与高度之比在9-12之间时,k值较大,再增大外半径与高度之比,k值增加不明显。
此处选择线圈外半径为高度的9倍,k值约为0.8。由此计算L1=175 μH。
取绕制线圈的铜带厚度为1 mm,线圈填充率一般为τ=0.7,线圈内半径受传动杆外径决定,传动杆需承受一定的拉伸应力,根据所用材料的特性可以确定其直径的最小值。从而可以确定线圈的内半径的最小值,此处选择内半径为R1= 30 mm。线圈高度为h1,外半径为R2=9×h1,匝数N=(R2-R1) ×0.7-1取整数。线圈实际电感为高度的单值函数L1'=f(h1)。
当h1=10 mm时,R2=90 mm,N=41。根据电感计算手册[6]计算线圈自感为L1=188 μH,比设计值大了7.5%。将匝数调整为40匝,其他尺寸不变,即稍微减小填充率,得到L1=179 μH,比计算电感L1大2.3%。在此尺寸下,计算线圈与斥力盘耦合系数约为0.8,与之前设定值吻合。
接下来考虑斥力盘所需厚度,趋肤深度δ为
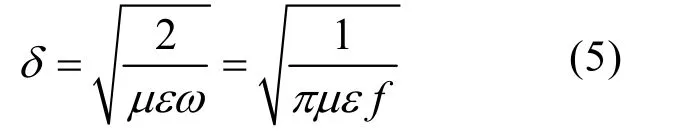
其中,μ和ε分别为斥力盘的磁导率和电导率,此处选择斥力盘为铝盘,有μ=4π×10-7,ε=3.3×107,频率f≈2π,由此算出δ≈ 4 mm 。因此在不考虑斥力盘机械强度的情况下,厚度h2可选为8 mm。
2 仿真验证
根据以上得到的斥力机构结构参数以及外电路参数,在ansoft Maxwell 2D瞬态场中进行仿真验证,仿真结果如图5所示。
由图5可以看出,3 mm行程时间约为1 ms,10 mm行程时间约为2.8 ms,满足设计要求。
3 总结
本文通过合理的简化假设,对一种较常用的斥力机构的物理过程进行理论计算,得出了由对机构的技术要求反求机构的结构尺寸以及电气参数的方法。并通过电磁场仿真软件ansoft Maxwell对所求参数进行仿真验证,验证结果证明设计结果满足要求,设计方法具有可靠性。对斥力机构的设计有一定的指导意义。
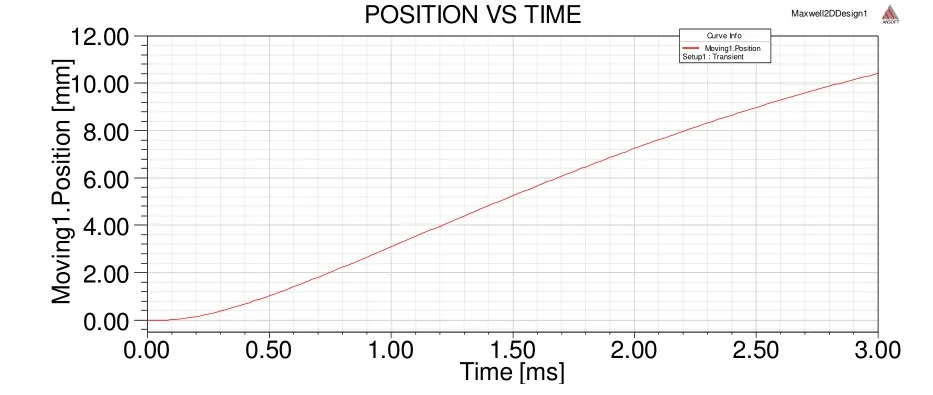
图5 ansoft仿真位移vs时间
[1]S.Basu, K.D.Srivastava. Analysis of a fast acting circuit breaker mechanism part II: electrical Aspects[J]. IEEE Transactions on Power Apparatus and Systems, 1972, PAS·91(3): 1197·1203, 1203-1211.
[2]TOSHIE TAKEUCHI, KENICHI KOYAMA,MITSURU TSUKIMA. Electromagnetic analysis coupled with motion for high-speed circuit breakers of eddy current repulsion using the Tableau Approach.Electrical Engineering in Japan, Vol. 152, No. 4, 2005
[3]李庆民, 刘卫东, 钱家骊. 电磁推力机构的一种分析方法. 电工技术学报, 2004, 19(2): 20-24.
[4]王子建, 何俊佳, 尹小根. 基于电磁斥力机构的10 kV 快速真空开关. 电工技术学报, 2009, 24(11):68-74
[5]Bart Roodenburg. First results from an electromagnetic (EM) drive high acceleration of a circuit breaker contact for a hybrid switch. ISBN: 90- 75815-08-5.
[6](苏)卡兰塔罗夫, (苏)采依特林. 电感计算手册[M].北京: 机械工业出版社, 1992.

