基于权值优选粒子滤波的雷达目标跟踪

白海东 黄双华 江艳阳 张社国

(1. 海军工程大学，武汉 430033； 2. 武汉军械士官学校，武汉 430075)

1 引言

在雷达目标跟踪的许多实际应用中，传感器所给出的目标参数是目标的斜距、方位角和高低角，导致了状态方程和量测方程至少有一个是非线性的，由此提出了对非线性跟踪方法的要求。

针对非线性问题，常用的算法有扩展卡尔曼滤波（EKF）、不敏卡尔曼滤波（UKF）、粒子滤波等，其中粒子滤波不受线性化误差和高斯噪声假定的限制，适用于任何环境下的任何状态模型和量测模型。

1993年由 Gordon[1]等提出的一种新的基于SIS的Bootstrap非线性滤波方法，奠定了粒子滤波算法的基础。近年来提出的许多非线性滤波新方法，都是基于SIS滤波思想，根据重要性函数的不同选择和重采样方法的不同，可以对粒子滤波器进行改进。

胡洪涛等[2]针对闪烁噪声情况下的目标跟踪，对于EKF算法和PF算法进行了仿真比较，本文在此基础上，使用一种基于权值优化的改进粒子滤波算法对雷达目标进行跟踪，并与标准的PF算法进行仿真比较。

2 粒子滤波

2.1 粒子滤波算法概述

粒子滤波算法是一种基于Monte Carlo仿真的最优回归贝叶斯滤波算法，采用数学语言描述如下：对于平稳的随机过程，假定k-1时刻系统的后验概率密度为p（xk-1|zk-1），依据一定原则选取n个随机样本点，k时刻获得测量信息后，经过状态和时间更新过程，n个粒子的后验概率密度可近似为p（xk|zk）。随着粒子数目的增加，粒子的概率密度函数逐渐逼近状态的概率密度函数，粒子滤波估计即达到了最优贝叶斯估计的效果。

2.2 重要概率密度函数

在粒子滤波中，最优的重要概率密度函数就是后验分布函数p（xkz1:k）本身，但是很难直接从p（xkz1:k）抽样得到样本。一种有效的解决方法是引入一个容易抽样的已知的概率密度分布函数q（x0:k|z1:k）作为重要概率密度函数，选择原则之一是使得重要性权重的方差最小。

本文选择一个非常常用的次优重要概率密度函数。

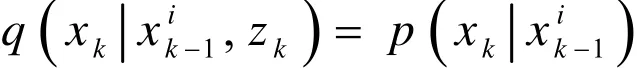
此时的重要性权重更新变为

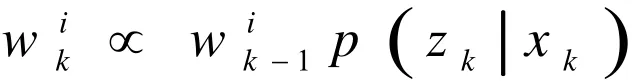
2.3 重采样

重采样的基本思想是：移除权重小的粒子和复制权重大的粒子，并重新分配权重，它将原有的粒子集合｛} 映射到新的取均匀权重的粒子集合

可以用图1来描述重采样算法的基本思想。

图1 重采样原理示意图

在图1中，以上面的一排圆圈表示重采样前的粒子，下面的一排圆圈表示重采样后的粒子，可以看出权重大的粒子被复制，权重小的粒子被剔除，经过重采样后所有的圆圈拥有相同的直径，表示具有相同的权重1/N（图中N取10）。

3 改进的粒子滤波算法

3.1 权值优选算法[3]

基本思想是：如果估计所需要的粒子为N个，那么抽取 Nt个粒子（Nt＞N），分别计算 Nt个粒子所对应的权值，选出其中权值最大的N个粒子参与状态估计，从而能够保证参与状态估计的粒子是最优秀的，此方法一定程度上解决了粒子的退化问题。

此方法的每一个粒子都是相互统计独立的，使得粒子集包含了更多的相异粒子，从而保证了粒子的多样性，优于普通重采样算法。

3.2 算法步骤

改进后的粒子滤波算法流程如下：

步骤1：初始化； k = 0 ,～p（x0），即根据已知概率p（x0）分布采样得到粒子集如下。

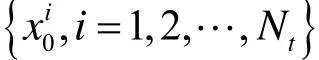
步骤 2：重要性权重计算；设定k:=k+1，采样：

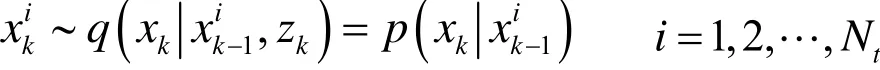
计算重要性权重：

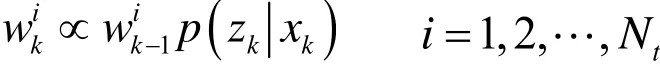
步骤3：选优；对Nt个粒子按照其权重大小进行排序，选出权重较大的N个粒子。

步骤4：归一化权值；

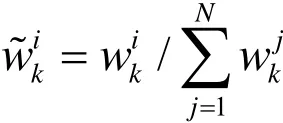
步骤5：状态估计；

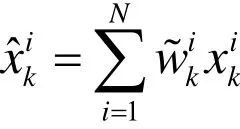
步骤6：归一化Nt个粒子的权值；

步骤 7：判断跟踪是否结束，是则退出本算法，否则返回步骤2进行下一步迭代。

4 雷达目标跟踪滤波模型

本文考虑一般的雷达目标跟踪问题。在直角坐标系下，设目标作匀速直线运动，雷达位于（x0,y0,z0）点。

状态方程为：

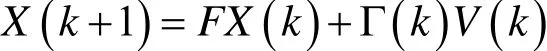
式中：F—状态转移矩阵；Γ(k)—过程噪声驱动矩阵；

V(k)—过程噪声，本文假设为零均值高斯噪声；T—采样间隔；X(k)—目标状态矢量，

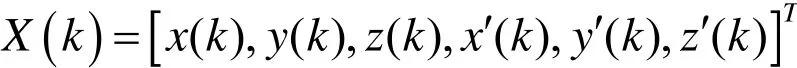
量测方程为：

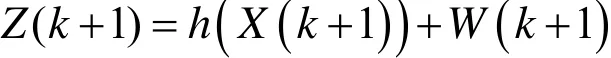
式中：

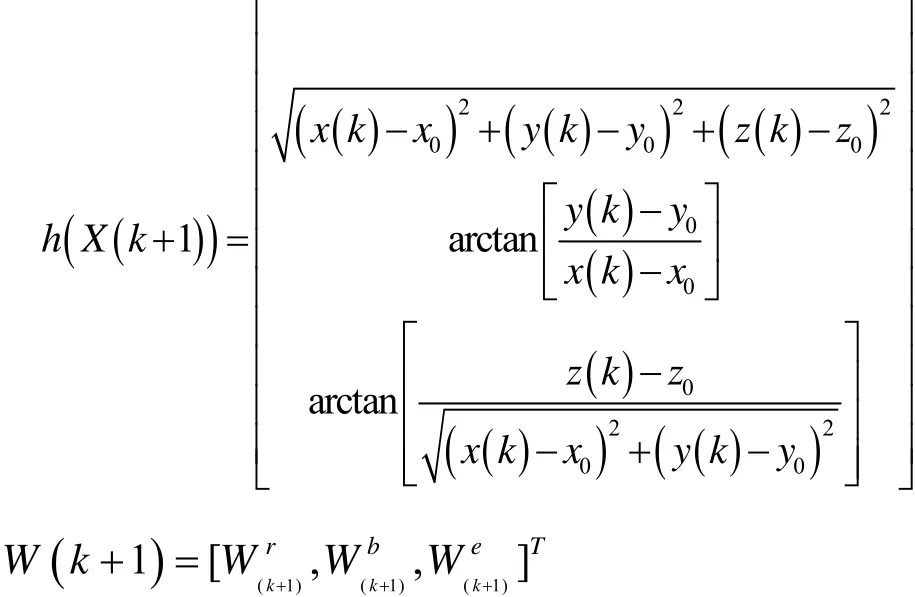
W(k+1)—测量噪声，其元素分别表示距离、方位、俯仰三个通道的测量噪声。

5 仿真分析

假设目标在三维空间内作匀速运动，初始位置为（50，50，10）km，初始速度为（0.3，-0.1，-0.04）km/s，雷达位于坐标原点，粒子数目N=100，采样周期为 1s。取热噪声的量测距离标准差为50m， 高低角和方位角的标准差都为1°，闪烁噪声的高低角和方位角标准差都为 5°，分别用 PF和改进 PF算法做100次蒙特卡洛仿真。得出目标的跟踪图形以及X方向位置和速度的误差绝对值曲线图形，Y、Z两个方向的误差曲线与X方向的类似，文中省略。

图2所示为分别利用PF和权值优选的PF算法对目标进行跟踪的三维图，图3和图4分别给出了X方向的位置和速度误差绝对值曲线；由误差绝对值曲线图可以看出，权值优选的 PF算法较标准PF算法具有更高的跟踪精度。

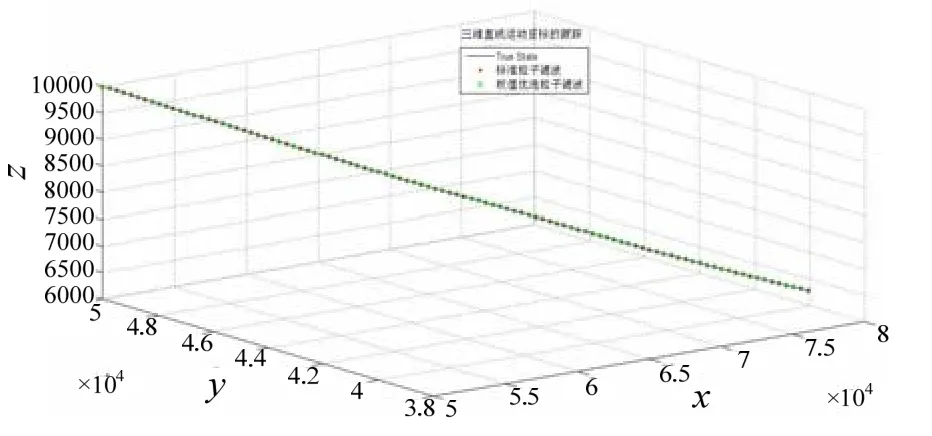
图2 三维直线运动目标的跟踪

由表1给出了N取不同值的情况下，利用两种算法跟踪的位置均方根误差比较。可以看出，随着N值的增大，X方向的位置均方误差在逐渐减小，说明N取较大值时，能够获得更高的跟踪精度。同时还可看出，改进的PF算法随着N值的增大，其精度逐渐接近标准PF算法。说明在N值较小的情况下，基于权值优选的粒子滤波算法具有更好的性能。这不仅可以节约系统开销，同时还为跟踪的实时性提供了保证。

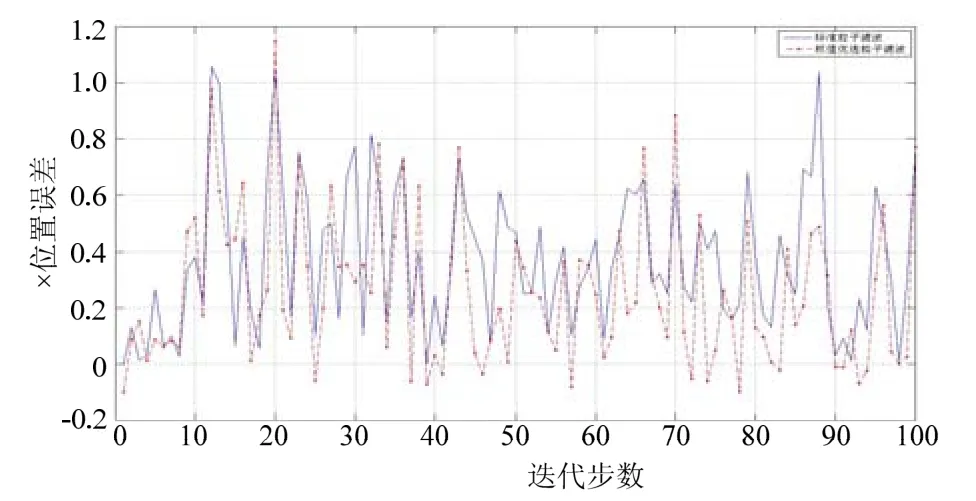
图3 X方向的位置误差绝对值曲线

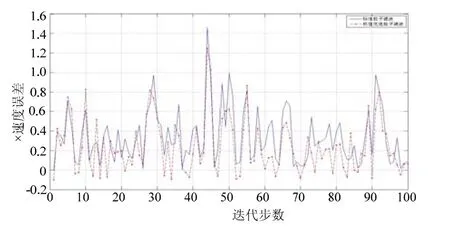
图4 X方向的速度误差绝对值曲线

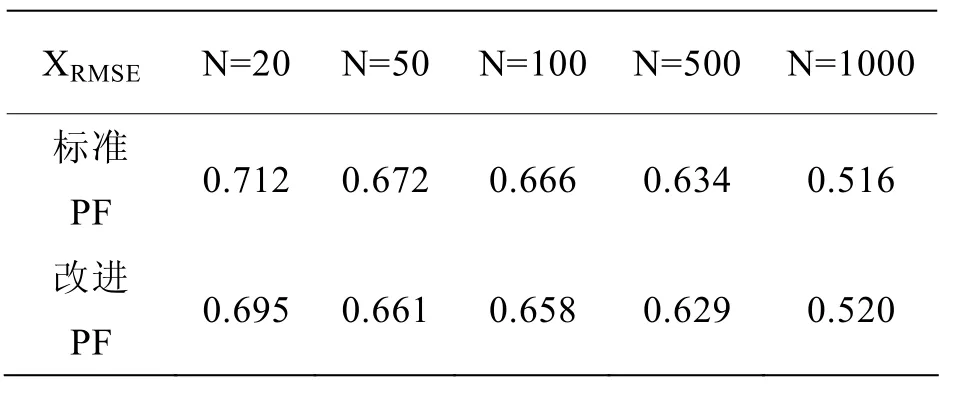
表1 N取不同值时X的位置均方误差

6 结束语

本文在闪烁噪声情况下，应用标准 PF算法和改进的 PF算法对雷达目标进行跟踪。仿真结果表明，改进的 PF算法在跟踪实时性要求较高的情况下具有更好的跟踪性能。

[1]Gordon N, Salmond D. Novel Approach to Non-linear and Non-Gaussian Bayesian State Estimation [J]. Proc of Institute Electric Engineering, 1993, 140(2): 107-113.

[2]胡洪涛, 敬忠良, 李安平, 胡士强. 非高斯条件下基于粒子滤波的目标跟踪[J]. 上海交通大学学报,2004, 38 (12): 1996-1999.

[3]朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010.6

[4]Gordon N, Salmond D. Bayesian State Estimation for Tracking and Guidance Using the Bootstrap Filter [J].J of Guidence, Control and Dynamics, 1995,18(6):1434-1443.

[5]N.P.K ostantinos, H. Dimitris. Advanced Signal Processing Handbook [M]. Boca Raton: CRC Press LLC, 2001:89-123.

[6]何友, 修建娟, 张晶炜, 关欣等. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2009

[7]吴宝成. 粒子滤波重采样算法研究及其应用[D]. 哈尔滨工业大学, 2006.6.

[8]戴丁樟.粒子滤波算法研究及其在目标跟踪中的应用[D]. 哈尔滨工业大学, 2006.6

[9]杨旭, 程杨, 曹喜滨, 杨涤. 粒子滤波在卫星轨道确定中的应用[J]. 控制理论与应用, 2005.8.

[10]朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010.6

[11]刘望生, 李亚安. 闪烁噪声下目标跟踪的改进粒子滤波算法[J]. 兵工学报, 2011, 32(1):91-95.

[12]李保国, 肖怀铁, 王远模, 刘义和, 付强. 角闪烁背景下基于粒子滤波器的跟踪研究[J]. 现代雷达,2006, 28(2): 54-56,77.

[13]胡士强, 敬忠良. 粒子滤波算法综述[J]. 控制与决策, 2005, 20(4): 361-365.

[14]王中训, 管旭军, 王德法. 非线性滤波算法在无源定位中的应用. 烟台大学学报(自然科学与工程版）,2007, 20(1): 35-39.