曲线插值的一种具有还圆性的细分方法
韩 靖, 韩旭里
(中南大学数学科学与计算技术学院,湖南 长沙 410083)
插值细分方法是一种离散数据插值,是计算机辅助几何设计中用于曲线曲面表示的重要方法。由于细分方法通常没有显式表达式,仅提供一个算法描述过程,具有简单、高效等特点,所以特别适用于计算机表示。近年来,细分方法引起越来越多的关注。
传统细分方法有切割磨光法和四点插值法,已经有许多学者作了相关研究[1-10]。切割磨光法是逼近型细分方法,具有逼近性,光滑性,保凸性等优点,其中Chaikin方法已被证明其极限曲线是由已知控制多边形所定义的二次 B样条曲线[1-2],但其极限曲线不经过控制顶点。文献[3]中的四点插值细分法,极限曲线可以表示三次B样条曲线。二次B样条曲线和三次B样条曲线作为分段多项式曲线,不能精确表示椭圆曲线。四点插值法是线性细分方法,简单易懂,但没有考虑控制多边形的几何形状,单从解析角度构造新点,不易对曲线的几何形状进行控制[8],且其极限曲线上可能有多余的拐点等[7]。
近年来,细分方法对保形性作了许多研究。为了使产生的细分曲线具有更好的保形性,文献[11]提出了一种基于法向量的细分方法,可以证明这种方法产生的曲线G1连续,只要选取合适的参数,此方法为保形细分算法,而且具有许多优美的性质,例如:可以插值在指定点的法向量、可以生成圆锥曲线、直边等。文献[12]提出了一种基于切向的几何插值型保凸细分方法,在细分的过程中,每条边所对应的新控制顶点由原控制顶点及其切向确定。该方法产生的极限曲线是G1连续的,且较为美观。由于保凸等性质对于线性细分较难达到,目前,非线性细分方法已成为研究的重点内容。
本文针对传统线性细分方法不能表示圆等非多项式曲线的情况,基于控制顶点的几何关系提出一种新的四点细分方法,如果初始控制顶点都取自同一个圆上,那么本方法所得极限曲线就是这个圆。
1 基于几何特性的四点细分法
细分法是通过不断地加入新点构造细分曲线。给定初始点列 {}i,四点插值型细分方法为

其中G表示一种构造,G的选取,也就是如何选择是插值细分方法的关键。
我们知道,过不在同一直线上的相邻三点可以作一个圆。这样,过相邻二插值点的圆弧有两条。我们的方法是取这两条圆弧的中点,将其加权平均得到新插值点。
1.1 计算插值点
对于第k层的点列{},若3点i不共线,则它们确定一个圆,记为。为边与边的垂直平分线 的交点,满足


得到新插值点,其中ω为权数,可用于调整曲线的形状。
结合式(2)~(7)即为式(1)中的函数G。
对于第k层的点列{,设第k层节点总数是n。当要生成封闭曲线时,点即;点。若要生成的曲线是开曲线,计算时,可用。这样保证了方法的可行性,也充分提取了控制顶点的信息。

图1 计算插值点
1.2 算法描述
作图时,新点的数量不需要无穷多,只需达到曲线在视觉上连续即可。定义Δ为任意相邻两点间的最大距离(包括初始点和最末点之间的距离)的上限,当点列中任意相邻两点间的距离都小于Δ时,曲线即达到视觉上连续,Δ的取值依赖于显示设备。该细分方法可用如下算法过程描述:
步 0 给定有0n个顶点的初始封闭凸多边形顶点点列及权数ω,令 :k= 0。
步 1 若要生成闭曲线,则令

显然,当所有初始控制顶点都取自同一个圆上时,新的插值点仍然在这个圆上,因此,本文的方法具有还圆性。
2 数值实例
作数值实例分析将本文方法与经典的切割磨光法与四点插值法以及文献[12]提出的基于几何切向的六点插值细分法对比作对比,其中切割磨光法取 Chaikin算法,即==1/4,细 分规则是

其中,N是初始顶点个数。四点插值法采用Dubuc格式[9]

文献[12]提出了一种基于几何切向的六点插值型细分方法,具有还圆性,以及保凸性等性质。
例1 取初如控制顶点(-1, -1), (0, 0), (0.5, 0),(1.8, 0), (3.2, 0.5), (4, -1),3点(0,0), (0.5,0), (1.8,0)共线,用本文方法取0.5ω=,曲线见图2,共线3点之间并非直线。曲线在共线点间的形状取决于相邻不共线点的偏离程度,偏离得越近,曲线越趋于直线。
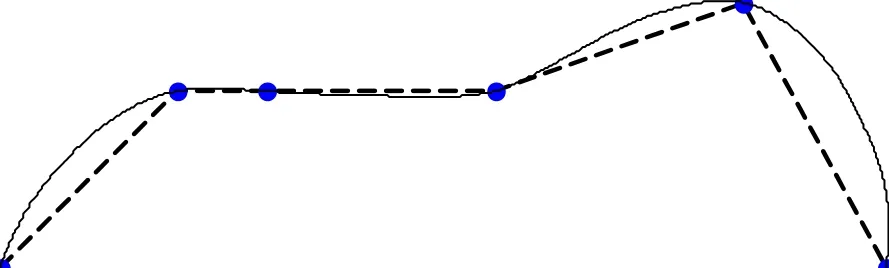
图2 本文方法例1
例 2 取初始控制顶点(1,0), (0,1), (-1,0),(0,-1),生成闭曲线。分别用本文方法取0.5ω=和经典的切割磨光法与四点插值法的Dubuc格式,曲线见图3、图4、图5。可见本文的方法可以完整的还圆,这从方法的推导过程也可得出,若所有初始点都在同一圆上,则相同,进而也与相同,都是圆上的点。切割磨光法与四点插值法都不具有还圆性。

图3 本文方法例2
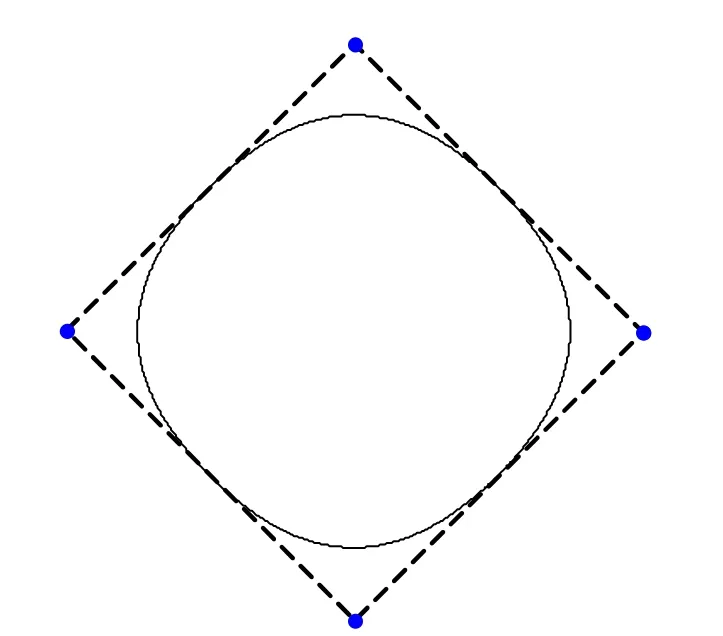
图4 切割磨光法例2

图5 四点插值法例2
例3 取初始控制顶点(0,0), (0.2425,1.3751),(-2.6241,0.9551), (-2.0944,-3.6276), (4.2784,-3.5900),(5.3480,4.4875), (-4.1888,7.2552), (-9.1844,-3.3429),(1.9397,-11.0004),用本文方法取0.5ω=和切割磨光法绘制开曲线,见图 6、图 7。本文方法可绘制出曲率半径变化比较光滑的螺旋,切割磨光法绘制曲线不经过控制顶点,曲线的曲率半径变化也不光滑,曲线形状更趋向控制多边形。
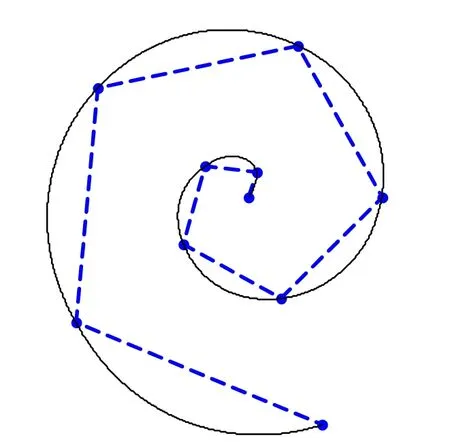
图6 本文方法例3

图7 切割磨光法例3
例4 给定初始控制多边形顶点为(3.0000,0),(0.3090,0.9511), (-0.8090,0.5878), (-0.8090,-0.5878),(0.3090,-0.9511),采用本文方法取0.2ω=、四点插值法和文献[12]提出的细分法绘制曲线,如图8、图9所示。与文献[12]的方法相比,本文方法的极限曲线更靠近控制多边形。
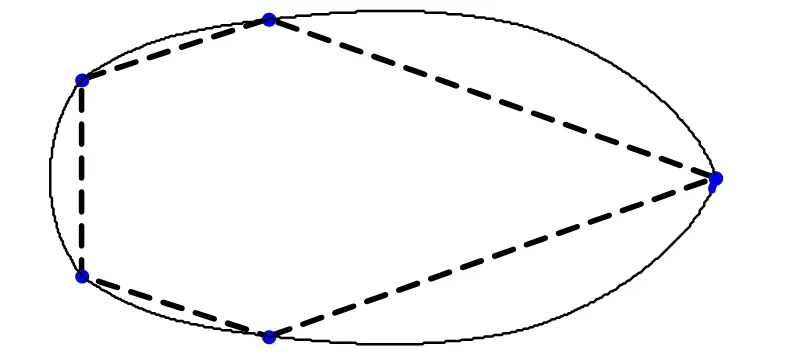
图8 本文方法例4
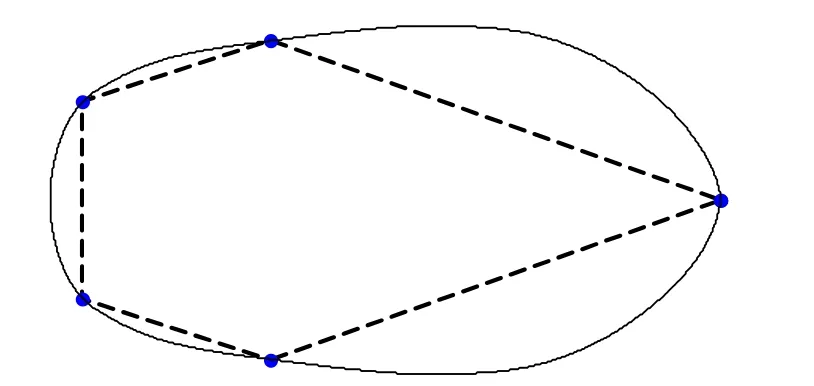
图9 文献[12]的方法例4
例 5 设初始控制顶点(1.0,1.0), (1.2,2.1),(2.0,2.5), (2.5,1.8), (3.0,1.5), (3.4,2.6), (4.0,3.2),(4.4,3.1), (5.0,2.0),用本文方法,分别取ω=0.3,ω= 0 .7绘制曲线。结果见图10、图11。对比可知ω取值越小,曲线越靠近控制多边形,但光滑性不佳;当ω增大,曲线远离控制多边形,且较为圆滑。

图10 例5中ω=0.3

图11 例5中ω=0.7
3 结 论
本文针对传统细分方法不能表示圆等非多项式曲线的限制,基于几何提出了一种含有一个参数的四点插值细分方法。这种方法的推导比较简单,给出了插值点计算公式和算法描述。与切割磨光法和四点插值法相比,本文的方法具有还圆性,可以实现保凸性,极限曲线较光顺。参数可以控制曲线与控制多边形的接近程度,参数取较小值时曲线靠近控制多边形。
由于本文提出的计算公式是一种非线性表示,方法的收敛性,光滑性等证明和与参数取值的关系还需要进一步研究。参数为0时曲线保凸这一条件较为严格,参数的取值范围应与保凸性具有某种关系。这些是接下来工作的重点。
[1]Chaikin G M. An algorithm for high speed curve generation [J]. Computer Graphics and Image Processing, 1974, 3(4): 346-349.
[2]Riesenfeld R F. On Chainik’s algorithm [J]. IEEE Computer Graphices and Applications, 1975, 4(3):304-310.
[3]Catmull E, Clark J. Recursively generated B-spline surfaces on arbitrary topological meshes [J].Computer Aided Design, 1978, 10(6): 350-355.
[4]Hassan M F, Ivrissimitzis I P, Dodgson N A, et al. An interpolating 4-point C2 ternary sationary subdivion scheme [J]. Computer Aided Geometric Design, 2002,19(5): 1-18.
[5]Dyna N, Levina D, Liu D. Interpolatory convexity-preserving subdivision schemes for curves and surfaces [J]. Computer-Aided Design, 1990,24(4): 221-216.
[6]Méhautéa A L, Utreras F I. Convexity-preserving interpolatory subdivision [J]. Computer Aided Geometric Design, 1994, 11(1): 17-37.
[7]Marinov M, Dyn N, Levin D. Geometrically controlled 4-point interpolatory Schemes [C]//Neil D,Michael S F, Malcolm S. Advances in Multiresolution for Geometric Modelling. London:Springer-Verlag, 2005: 301-315.
[8]Dyn N, Levin D, John A. A 4-point interpolatory subdivision scheme for curve design [J]. Computer Aided Geometric Design, 1987, 4(4): 257-268.
[9]Dubuc S. Interpolation through an iterative scheme [J].Journal of Mathematical Analysis and Applications,1986, 114(1): 185-204.
[10]曹 沅. 四点插值细分算法极限曲线曲面C2连续的充分必要条件[J]. 计算机辅助几何设计与图形学学报, 2003, 15(8): 961-966.
[11]Yang Xunnian. Normal based subdivision scheme for curve design [J]. Computer Aided Geometric Design,2006, 23(4): 243-260.
[12]邓重阳, 汪国昭. 曲线插值的一种保凸细分方法[J].计算机辅助设计与图形学学报, 2009, 21(8):1042-1046.

